
- •Структура педагогического эксперимента
- •Математическая обработка педагогического эксперимента
- •Характеристики рассеивания
- •Корреляционное отношение
- •Коэффициент вариации
- •Доверительный интервал
- •Ранговые корреляции и взаимосвязи в педагогических экспериментах
- •Коэффициент корреляции Пирсона
- •Корреляционные матрицы и графы
- •Коэффициент конкордации
- •Статистические гипотезы
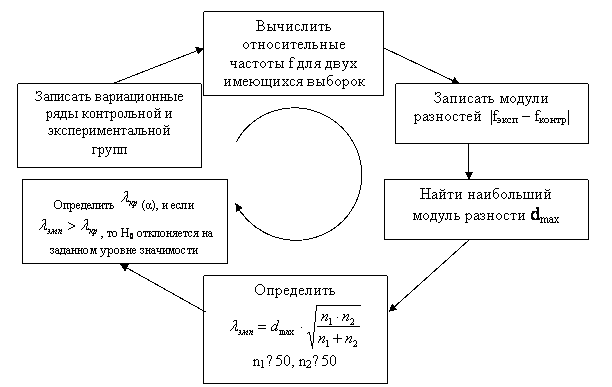
- •Критерий Крамера-Уэлча
- •Критерий Фишера
- •Проверка нормальности распределения
- •Критерий Фридмана
- •Критерий Пейджа
- •Значимость коэффициента корреляции
- •Существенность коэффициента конкордации
Проверка нормальности распределения
Для
проверки распределения на предмет
соответствия нормальному закону
вычисляют выборочную среднюю
![]() и
среднее квадратическое отклонение σ,
а затем вычисляют теоретические частоты
по следующей формуле:
и
среднее квадратическое отклонение σ,
а затем вычисляют теоретические частоты
по следующей формуле:
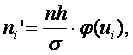
где:
n – объём выборки, h – шаг (разность между
двумя соседними вариантами),
![]()
![]()
Рассмотрим пример. В результате выборочного обследования стажа работы профессорско-преподавательского состава получены следующие данные:
Стаж работы (лет) |
0-4 |
4-8 |
8-12 |
12-16 |
16-20 |
20-24 |
24-28 |
28-32 |
Число преподавателей |
3 |
8 |
25 |
40 |
46 |
31 |
6 |
2 |
Выяснить, является ли распределение стажа работы нормальным на уровне значимости α=0,01.
Для решения поставленной задачи перейдем от заданного интервального распределения к распределению равноотстоящих вариант и вычислим выборочную среднюю и выборочное среднее квадратическое отклонение.
n=161,
![]()
![]() а
а
![]()
Составим расчетную таблицу, заполняя её последовательно по столбцам слева направо:
i |
xi |
|
|
|
ni |
(ni-ni’)2 |
|
1 |
2 |
-2,58 |
0,014 |
1,66 |
3 |
1,8 |
1,08 |
2 |
6 |
-1,84 |
0,073 |
8,66 |
8 |
0,44 |
0,05 |
3 |
10 |
-1,1 |
0,218 |
25,85 |
25 |
0,72 |
0,033 |
4 |
14 |
-0,37 |
0,373 |
44,24 |
40 |
17,89 |
0,41 |
5 |
18 |
0,37 |
0,373 |
44,24 |
46 |
3,1 |
0,07 |
6 |
22 |
1,1 |
0,218 |
25,85 |
31 |
26,52 |
1,03 |
7 |
26 |
1,84 |
0,073 |
8,66 |
6 |
7,08 |
0,82 |
8 |
30 |
2,58 |
0,014 |
1,66 |
2 |
0,12 |
0,07 |
Σ |
|
|
|
|
161 |
|
|
По таблице критических точек распределения по уровню значимости α=0,01 и числу степеней свободы k=s-3=8-3=5 находим критическую точку критической области
![]()
Так
как
![]() то
гипотезу о нормальном распределении
генеральной совокупности принимаем.
то
гипотезу о нормальном распределении
генеральной совокупности принимаем.
Критерий Манна-Уитни U-критерий Манна-Уитни используется для оценки различий между двумя малыми выборками (n1,n2≥3 или n1=2, n2≥5) по уровню количественно измеряемого признака. При этом первой выборкой принято считать ту, где значение признака больше. Нулевая гипотеза H0={уровень признака во второй выборке не ниже уровня признака в первой выборке}; альтернативная гипотеза – H1={уровень признака во второй выборке ниже уровня признака в первой выборке}. Рассмотрим алгоритм применения U-критерия Манна-Уитни:
Рассмотрим использование U критерия Манна-Уитни на примере. Проведение срезовой контрольной работы по математике (алгебра и геометрия) в средней общеобразовательной школе дало следующие результаты по 10-балльной шкале для класса, обучающегося по программе «Развивающего обучения» (7 «Б»), и класса, обучающегося по традиционной системе (7 «А»):
Определите, превосходят ли учащиеся 7 «Б» учащихся 7 «А» по уровню знаний по математике. Сравнение результатов показывает, что баллы, полученный за контрольную работу, в 7 «Б» классе несколько выше, поэтому первой считаем выборку результатов 7 «Б» класса. Таким образом, нам требуется определить, можно ли считать имеющуюся разницу между баллами существенной. Если можно, то это будет означать, что класс, обучающийся по системе «развивающего обучения» имеет более качественные знания по математике. В противном случае, на выбранном уровне значимости различие окажется несущественным. Для оценки различий между двумя малыми выборками (в данном примере их объёмы равны: n1=12, n2=11) используем критерий Манна-Уитни. Проранжируем представленную таблицу:
При
ранжировании объединяем две выборки
в одну. Ранги присваиваются в порядке
возрастания значения измеряемой
величины, т.е. наименьшему рангу
соответствует наименьший балл. Заметим,
что в случае совпадения баллов для
нескольких учеников ранг такого балла
следует считать, как среднее
арифметическое тех позиций, которые
занимают данные баллы при их расположении
в порядке возрастания. Например, 4
балла получили 3 ученика (см. таблицу).
Значит, первые 3 позиции в расположении
займёт балл, равный 4. Поэтому ранг для
4 баллов – это среднее арифметическое
для позиций 1, 2 и 3, или:
Используя предложенный принцип ранжирования, получим таблицу рангов. Заметим, что выбор среднего арифметического в качестве ранга применяется при любом ранжировании, в том числе необходимого и для вычисления других критериев достоверности или же коэффициента корреляции Спирмена. Чтобы использовать критерий Манна-Уитни, рассчитаем суммы рангов рассматриваемых выборок (см. таблицу). Сумма для первой выборки равна 168,5, для второй – 107,5. Обозначим наибольшую из этих сумм через Tx (Tx=168.5). Среди объёмов n1 и n2 выборок наибольший обозначим nx. Этих данных достаточно, чтобы воспользоваться формулой расчёта эмпирического значения критерия:
Tx=168,5, nx=12>11=n2. Тогда:
Критическое значение критерия находим по специальной таблице. Пусть уровень значимости равен 0.05. Гипотеза H0 о незначительности различий между баллами двух классов принимается, если uкр<uэмп. В противном случае H0 отвергается и различие определяется как существенное.
Следовательно, различия в уровне знаний по математике среди учащихся можно считать несущественными. Схема использования критерия Манна-Уитни выглядит следующим образом
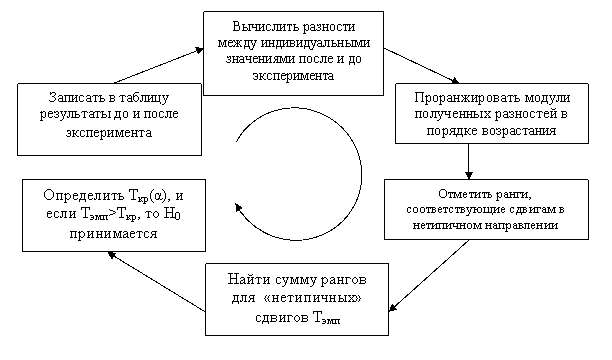
Критерий Вилкоксона Критерий применяется для сопоставления показателей изменений в двух разных условиях на одной и той же выборке испытуемых. С его помощью можно определить, является ли сдвиг показателя в каком-то одном направлении более существенным, чем в другом. Нулевая гипотеза H0={существенность сдвигов в типичном направлении не превосходит существенности сдвигов в нетипичном направлении}. На объём выборки накладывается следующее условие: 5≤n≤50. Для демонстрации применения критерия определим значимость различий изменений вербальной памяти до и после иппотерапии (в баллах), используя следующие данные:
Воспользуемся следующим алгоритмом: 1. Вычислим разности между индивидуальными значениями показателя после проведения эксперимента и до него. 2. Для полученных разностей найдём их модули и произведём их ранжирование в порядке возрастания. 3. Отметим ранги, соответствующие сдвигам в нетипичном направлении. Например, если в большинстве случаев после проведения эксперимента наблюдалось увеличение измеряемого параметра, то его уменьшение следует считать нетипичным сдвигом. После выполнения указанных действий исходную таблицу можно представить следующим образом (нетипичные сдвиги выделены шрифтом).
Эмпирическое значение критерия определяется как сумма рангов, соответствующих нетипичным сдвигам. В рассмотренном примере имеется только один такой сдвиг (см. таблицу), которому соответствует ранг, равный 5. Поэтому эмпирическое значение критерия будет численно равно этому рангу: Tэмп=5. Критическое значение следует искать в специальной таблице. Пусть уровень значимости равен 0.05. По таблице находим, что Tкр(0.05)=10. Сравним полученные значения критерия. Если критическое значение не превосходит эмпирического, то на данном уровне значимости отсутствуют основания для отклонения нулевой гипотезы о несущественности различий. Иначе, нулевая гипотеза отвергается. Т.к. Tэмп=5<10=Tкр(0,05), то нулевую гипотезу следует отвергнуть и считать различия существенными. Таким образом, схема применения критерия Вилкоксона будет иметь следующий вид:
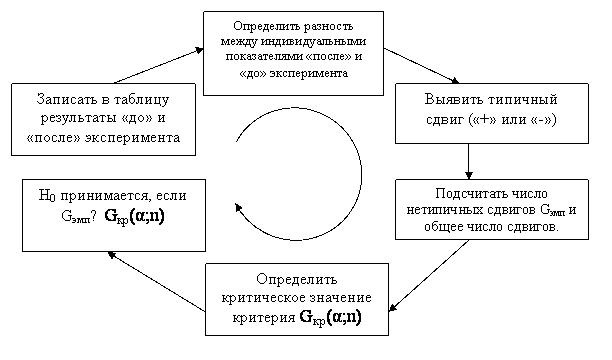
Критерий Вилкоксона позволяет установить не только направленность изменений, но и их выраженность. Следующий рассматриваемый нами критерий служит только для определения направления изменения в двух связанных выборках. Критерий знаков Сравнивая результаты «до» и «после» какого-либо воздействия на учащихся, педагог видит тенденции повторного измерения – большинство показателей могут увеличиваться или, напротив, уменьшаться. Для того чтобы доказать эффективность воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей. Одним из наиболее простых критериев различия является критерий знаков G. Он дает возможность установить, на сколько однонаправленно изменяются значения признака при повторном измерении связанной однородной выборки. Критерий знаков применяется к данным, полученным в ранговой, интервальной и шкале отношений. В остальных случаях, когда сдвиги могут быть определены количественно и варьируются в достаточно широком диапазоне, лучше применять критерий Вилкоксона. Решим с использованием критерия знаков следующую задачу. Результаты измерения уровня тревожности до и после проведения тренинга в группе испытуемых отображены в таблице.
Определить, является ли изменение уровня тревожности статистически значимым. Сдвигом называется разность между значениями измеряемого параметра «после» и «до» проведения эксперимента. В качестве нулевой гипотезы примем: H0={преобладание типичного направления сдвига является случайным}; альтернативная гипотеза – H1={преобладание типичного направления сдвига не является случайным}. Для проверки нулевой гипотезы определяют типичный сдвиг ("+" или "-") и считают число (количество) типичных и нетипичных сдвигов. В примере число положительных сдвигов превосходит количество сдвигов в отрицательном направлении. Поэтому в данной задаче типичным является положительный сдвиг. Из таблицы видно, что число n таких сдвигов равно 8. Эмпирическое значение критерия определяется, как число нетипичных сдвигов. В нашем случае Gэмп=5. Критическое значение критерия Gкр(α;n) определяют по специальной таблице, где n – общее число сдвигов, т.е. объем выборки. Пусть уровень значимости α=0,05. Тогда Gкр(0,05; 13)=3. Нулевая гипотеза принимается, если Gэмп≥Gкр(α;n). Поскольку Gэмп=5>3= Gкр(0,05; 13), то нулевая гипотеза принимается, и типичный сдвиг является случайным на выбранном уровне значимости. Применение критерия знаков можно представить в виде следующей схемы:
Заметим, что количество измерений должно быть не меньше 5 и не больше 300. При равенстве типичных и нетипичных сдвигов критерий знаков неприменим. Критерий Макнамары Этот критерий предназначен для работы с данными, полученными в самой простой из номинальных – дихотомической шкале, допускающей два типа ответов – «да» или «нет» (кодируются цифрами 1 и 0 соответственно). Экспериментальные данные (или данные опроса), полученные педагогом в результате двукратного опроса, записываются в четырехпольную таблицу формата 2х2:
Поля в этих таблицах заполняются числами: A – количество учащихся, которые до и после эксперимента ответили «да». B – количество учащихся, которые до эксперимента ответили «да», а после эксперимента – «нет». C – количество учащихся, которые до эксперимента ответили «нет», а после эксперимента – «да». D – количество учащихся, которые до и после эксперимента ответили «нет». Расчет эмпирического значения Mэмп критерия производится (для B≠C) следующим образом: а) если B+C=n≤20, то Mэмп находится по таблице M(n,m), где m=min(В,C). б) если B+C>20, то Mэмп вычисляется по формуле
При B=C рекомендуется использовать χ2-критерий. Опишем алгоритм применения критерия Макнамары следующей схемой:
Нулевая гипотеза H0={различие значений исследуемого показателя до и после эксперимента несущественно}; альтернативная гипотеза – H1={различие показателя до и после эксперимента существенно}. Рассмотрим применение данного критерия на примере. Проведение пробного тестирования по математике в форме ЕГЭ в первой и второй четверти дало следующие результаты.
Можно ли сказать, что справляемость учащихся изменилась существенно? В приведенном примере B≠C, поэтому применение критерия Макнамары допустимо. Вычислим сумму B+C=19+31=50>20, поэтому вычисляем:
Пусть уровень значимости α=0,05. Тогда Mкр=3,84>2,88=Mэмп. Следовательно, нулевая гипотеза на данном уровне значимости отклоняется, и различия в уровне справляемости существенны. В предыдущих примерах было показано, каким образом можно оценить существенность изменения того или иного признака на основе сравнения двух выборок. Однако, нередко возникают ситуации, когда необходимо оценить различия сразу в нескольких (более двух) выборках. Для такой цели в математической статистике также имеется ряд критериев достоверности (критерий Крускала-Уоллиса, Фридмана, Пейджа и др.).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

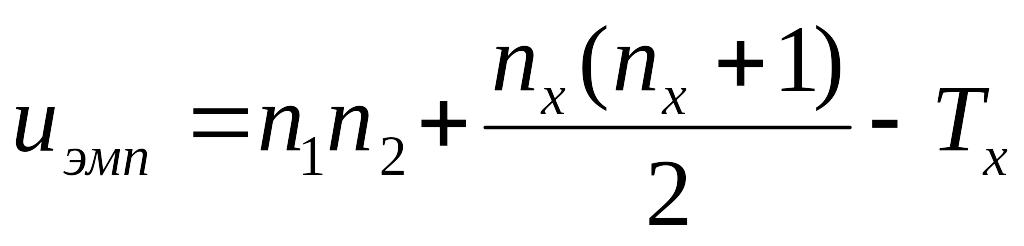
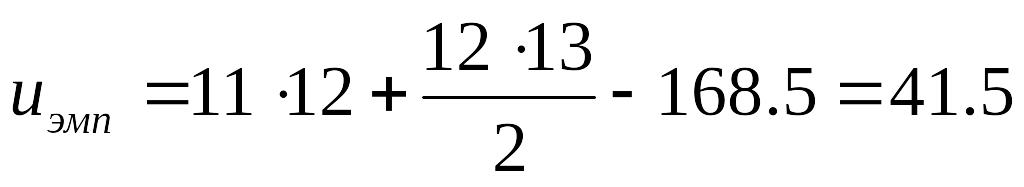
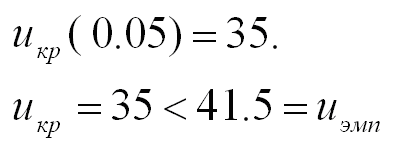
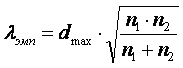













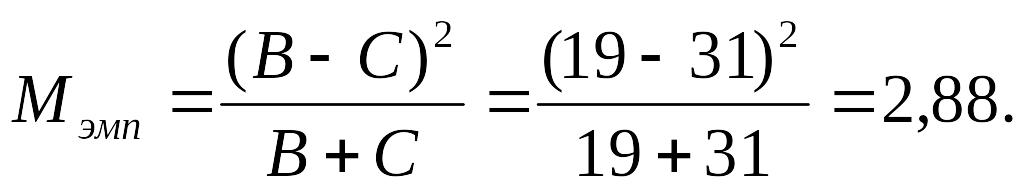
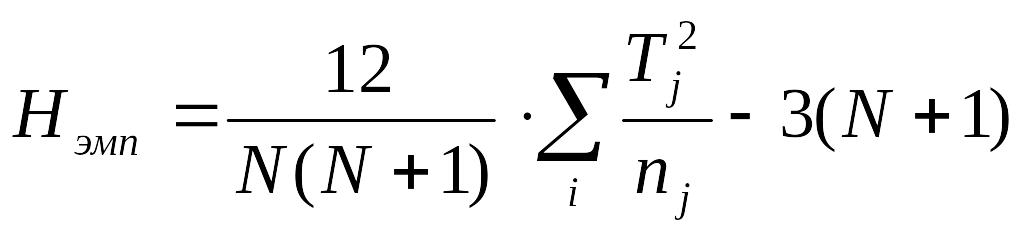 ,
где N
– общее количество испытуемых
(N=27),
Tj
– сумма рангов в j-ой
строке, nj
– число испытуемых в j-ой
группе.
,
где N
– общее количество испытуемых
(N=27),
Tj
– сумма рангов в j-ой
строке, nj
– число испытуемых в j-ой
группе.
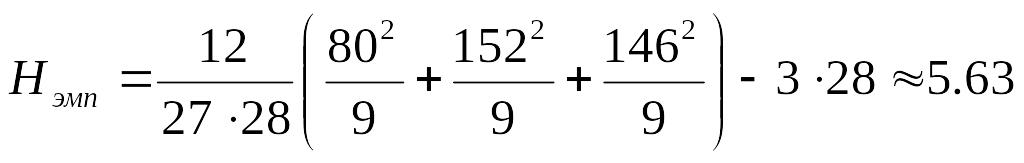 В рассматриваемом примере количество
испытуемых во всех группах одинаково
и равно 9. На практике можно использовать
и выборки разных объёмов.
В рассматриваемом примере количество
испытуемых во всех группах одинаково
и равно 9. На практике можно использовать
и выборки разных объёмов.





