Критерий Крамера-Уэлча

В педагогике иногда t-критерий Стьюдента заменяют более простым критерием Крамера-Уэлча. Эмпирическое значение данного критерия рассчитывается по следующей формуле:

         Следует заметить, что эмпирическое значение критерия Крамера-Уэлча есть приближенное значение эмпирического значения  t-критерия Стьюдента. Легко видеть, что при достаточно больших n₁ и n₂ справедливо следующее приближенное равенство:

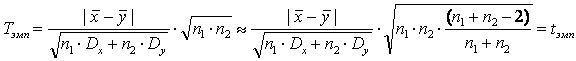
Заметим, что критические значения для критерия Крамера-Уэлча зависят только от уровня значимости α и выражаются через критические значения t-критерия Стьюдента следующим образом:

 

Поэтому алгоритм и схема использования критерия Крамера-Уэлча будут аналогичными, как и для критерия Стьюдента.

Рассмотрим использование данного критерия для данных из предыдущего примера.

Найдем эмпирическое значение для критерия Крамера-Уэлча:

 

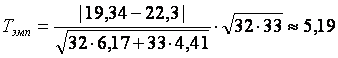
         Поскольку T_кр(0,01)=2,58<5,19=T_эмп, то сравниваемые выборочные средние отличаются значимо.

Рассмотренный пример показывает, что эмпирические значения t-критерия Стьюдента и критерия Крамера-Уэлча в незначительной мере отличаются друг от друга. При этом очевидно, что чем больше объёмы выборок, тем меньше отличия числовых значений данных критериев.

Критерий Фишера

F - критерий Фишера является параметричесикм критерием и используется для сравнения дисперсий двух вариационных рядов. Эмпирическое значение критерия  вычисляется по формуле:

где - большая дисперсия, - меньшая дисперсия рассматриваемых вариационных рядов.

         Если вычисленное значение критерия F_эмп больше критического для определенного уровня значимости и соответствующих чисел степеней свободы для числителя и знаменателя, то дисперсии считаются различными. Иными словами, проверяется гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: H₀={D_x=D_y}.

         Критическое значение критерия Фишера следует определять по специальной таблице, исходя из уровня значимости α и степеней свободы числителя (n₁-1) и знаменателя (n₂-1).

         Проиллюстрируем применение критерия Фишера на следующем примере. Дисперсия такого показателя, как стрессоустойчивость для учителей составила 6,17 (n₁=32), а для менеджеров 4,41 (n₂=33). Определим, можно ли считать уровень дисперсий примерно одинаковым для данных выборок на уровне значимости 0,05.

         Для ответа на поставленный вопрос определим эмпирическое значение критерия:  При этом критическое значение критерия F_кр(0,05;31;32)=2.

         Таким образом, F_эмп=1,4<2=F_кр, поэтому нулевая гипотеза о равенстве генеральных дисперсий на уровне значимости 0,05 принимается.

 Непараметрические критерии

Непараметрические критерии не содержат расчёта параметров распределения и основаны на оперировании частотами или рангами. Непараметрические критерии, как правило, менее сложны в вычислениях и могут быть измерены в любой шкале, начиная от шкалы наименований.

Критерий Пирсона Критерий согласия Пирсона позволяет осуществлять проверку эмпирического и теоретического (либо другого эмпирического) распределений одного признака. Данный критерий применяется, в основном, в двух случаях: - Для сопоставления эмпирического распределения признака с теоретическим распределением (нормальным, показательным, равномерным либо каким-то иным законом); - Для сопоставления двух эмпирических распределений одного и того же признака.          Идея метода – определение степени расхождения соответствующих частот ni и ; чем больше это расхождение, тем больше значение Объемы выборок должны быть не меньше 50 и необходимо равенство сумм частот          Нулевая гипотеза H0={два распределения практически не различаются между собой}; альтернативная гипотеза – H1={расхождение между распределениями существенно}.          Приведем схему применения критерия для сопоставления двух эмпирических распределений:          Рассмотрим применение критерия на следующем примере.          Среди школьников с 1 по 7 класс в течение двух недель проводился опрос об удовлетворенности собственными оценками. Результаты опроса представлены в таблице: Номер возрастного интервала (соответствует классу) Число удовлетворенных оценками в первую неделю исследования Число удовлетворенных оценками на второй неделе исследования 1 16 17 2 13 13 3 8 9 4 11 9 5 4 3 6 3 4 7 3 3   Можно ли считать, что эмпирическое распределение на первой неделе исследования согласуется с эмпирическим распределением на второй неделе исследования, т.е. структура удовлетворенности ответами учащихся сохранилась в течение данного времени?          Пусть уровень значимости равен 0,05. 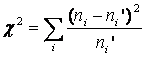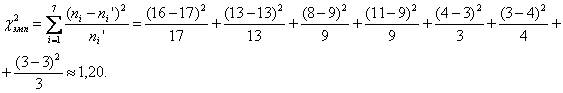Вычислим эмпирическое значение критерия:           По таблице критических точек распределения  по заданному уровню значимости 0,05 и числу степеней свободы k=7-1 находим критическую точку          Поскольку то нет оснований отвергать нулевую гипотезу об одинаковом распределении мнений учащихся о своей успеваемости в разные недели.