Коэффициент корреляции Пирсона

Для определения корреляционной зависимости между двумя случайными величинами используют коэффициент корреляции Пирсона. Заметим, что понятие корреляции является одним из основных понятий теории вероятностей и математической статистики; оно было введено Гальтоном и Пирсоном.

Рассмотрим пример распределения оценок, для которого использование коэффициента Спирмена нецелесообразно.

 

ученик	1	2	3	4	5
ЕГЭ по физике	98	40	39	39	35
ЕГЭ по математике	92	94	83	80	55

 

В указанной таблице имеет место «скачок» в оценках по физике, выраженный в сильном различии оценок первого и второго учеников. Разница между этими оценками существенна и порождает неравномерность распределения оценок.

         В подобных случаях рекомендуется применять выборочный коэффициент корреляции r Пирсона. Для его расчёта необходимо найти особую величину k(X,Y), называемую ковариацией.

         Пусть величина X принимает значения x₁, x₂, …, x_n, а величина Y – y₁, y₂, …, y_m. Тогда можно найти выборочную среднюю для величины X и выборочную среднюю для величины Y. Если n_ij – это частота, с которой встречается в полученных выборках x_i и y_j, а n – объём выборки ( ), то ковариация k(X,Y) вычисляется по формуле:

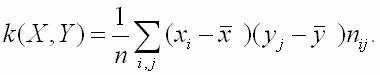
         Для малых выборок ковариацию удобно находить с помощью ковариационного графа, для построения которого необходимо вычислить выборочные средние для величин X, Y и относительные частоты . Ковариационный граф имеет вид:

Таким образом, ковариацию k(X,Y) можно находить как вес всего ковариационного графа. Заметим, что по корреляционному графу удобно находить и дисперсии случайных величин, которые также необходимы для вычисления коэффициента корреляции Пирсона.

         Выборочный коэффициент корреляции определяется по формуле:

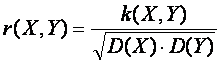
Для иллюстрации использования коэффициента корреляции и применения ковариационного графа рассмотрим пример. В выпускном классе проводились контрольные работы по физике и математике, которые дали следующие результаты:

 

	«2»	«3»	«4»	«5»
«2»	1 чел.	2 чел.	1 чел.	-
«3»	1 чел.	4 чел.	2 чел.	-
«4»	-	1 чел.	3 чел.	4 чел.
«5»	-	1 чел.	3 чел.	2 чел.

Определим характер и силу связи между оценками в проведенных работах. Для этого найдём выборочную ковариацию и коэффициент корреляции.

Объём выборки равен n=25, т.к. контрольные работы писали 25 человек (сумма всех данных в таблице).

Пусть X – это оценки по физике, а Y – оценки по математике. Тогда по имеющейся таблице составим две таблицы (по строкам и столбцам) для нахождения выборочных средних.

По физике (величина X):

Оценка	«2»	«3»	«4»	«5»
Количество чел.	4	7	8	6

По математике (величина Y):

Оценка	«2»	«3»	«4»	«5»
Количество чел.	2	8	9	6

По данным таблицам находим выборочные средние:

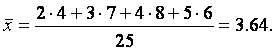
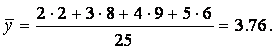
После этого можно составить ковариационный граф.

Из построенного графа находим ковариацию:

        По корреляционному графу находим и выборочные дисперсии: D(X)=(-1,64)²(0,04+0,08+0,04)+(-0,64)²(0,04+0,16+0,08)+ +(0,36)²(0,04+0,12+0,16)+(1,36)²(0,04+0,12+0,08)=1.03, аналогично вычисляем дисперсию D(Y)=0.82.

Поэтому 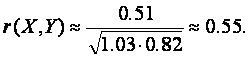 Таким образом, между оценками по физике и математике в данной выборке существует прямая связь средней силы.

         Ранговая корреляция Спирмена и выборочный коэффициент корреляции позволяют нам определить характер и силу связи для двух измеряемых величин. Но на практике педагогические и психологические эксперименты зачастую производят измерения большего количества величин. Например, тестирование учащихся может проводиться по таким параметрам, как трудолюбие, усидчивость, память, качество речи и т.д. Для того чтобы узнать, каким образом связаны все эти качества, можно использовать два следующих метода:

1.     Рассматривают попарные связи и иллюстрируют их на корреляционных матрицах или корреляционных графах;

2.     Находят множественный коэффициент ранговой корреляции – коэффициент конкордации.