Значимость коэффициента корреляции

Из двумерной генеральной совокупности (X, Y) извлечена выборка объёма n и по ней найден выборочный коэффициент корреляции r_в, который оказался отличным от нуля. Поскольку выборка отобрана случайно, то нельзя заключить, что коэффициент корреляции генеральной совокупности r также отличен от нуля. Возникает необходимость при данном уровне значимости α проверить нулевую гипотезу H₀={r=0} о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе H₁={r_s≠0}.

В качестве критерия проверки нулевой гипотезы применяют случайную величину

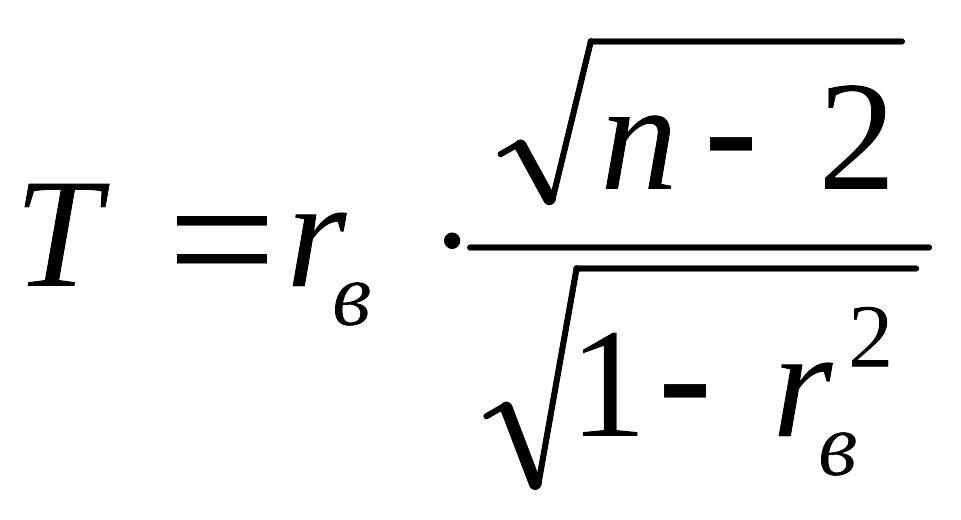
Величина T при справедливости нулевой гипотезы имеет распределение Стьюдента с k=n-2 степенями свободы. Поэтому вычисляется эмпирическое значение критерия:

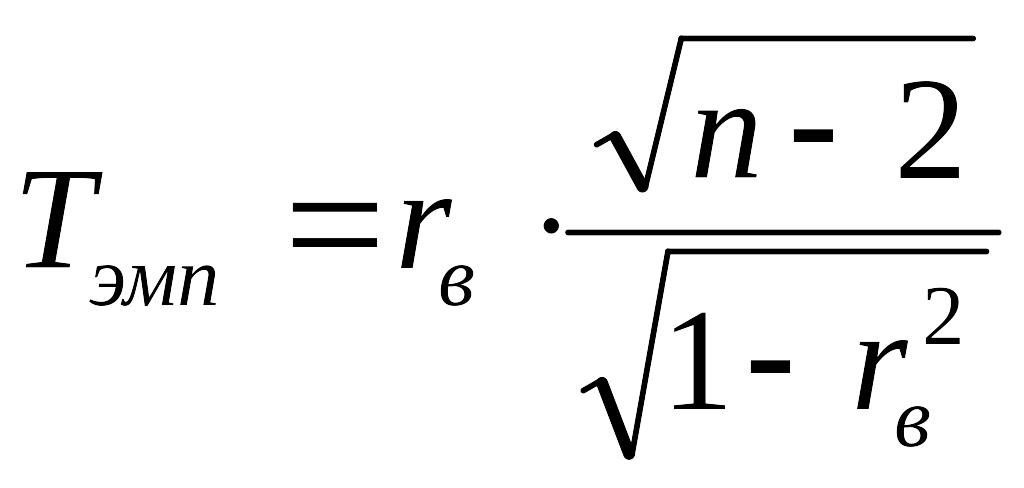
и по таблице критических точек распределения Стьюдента по выбранному уровню значимости α и числу степеней свободы k=n-2 находят критическую точку t_кр(α;k).

Если |T_эмп|>t_кр, то нулевую гипотезу отвергают, и выборочный коэффициент корреляции значимо отличается от нуля, а X и Y коррелированны, т.е. связаны линейной зависимостью.

Если |T_эмп|≤t_кр, то нет оснований отвергать нулевую гипотезу и говорят, что выборочный коэффициент корреляции незначим, а X и Y некоррелированы, т.е. не связаны линейной зависимостью.

Проиллюстрируем использование t-распределения Стьюдента для определения значимости коэффициента корреляции. Для этого воспользуемся рассмотренной ранее задачей и определим, можно ли считать связь между результатами ЕГЭ по русскому языку и математике значимой.

В данном примере коэффициент корреляции Спирмена равен r_s=0.75. Решим поставленную задачу на уровне значимости Для этого выдвинем основную гипотезу H₀, утверждающую, что связь несущественна: H₀={r_s=0} и H₁={r_s≠0}. Чтобы оценить истинность этой гипотезы на заданном уровне значимости, необходимо сначала найти критическое значение t_кр( ;k) критерия, которое определяется по специальной таблице. t_кр зависит от уровня значимости и степени свободы k, равной в данном случае n-2, где n – объём выборки. Т.к. и n=7, то по таблице находим t_кр= t_кр(0,05; 5) 2.57.

Далее следует воспользоваться формулой:

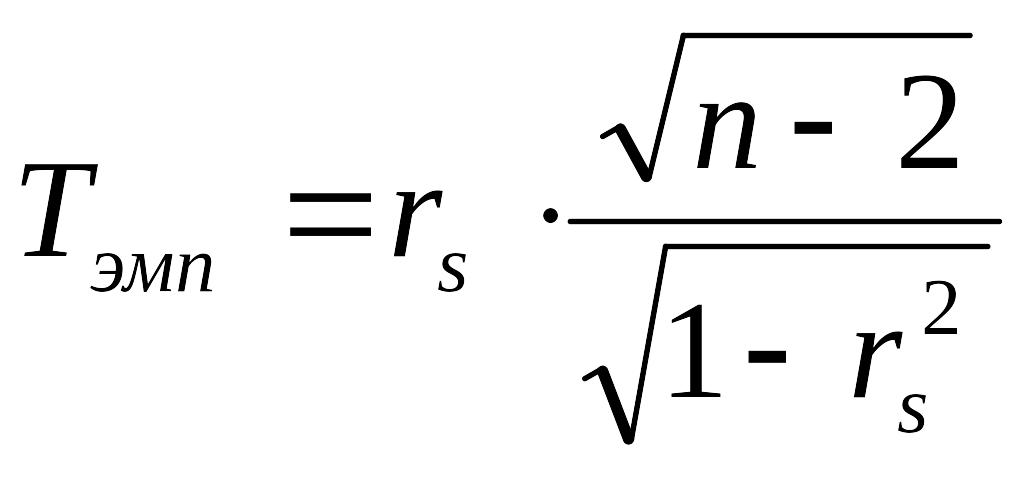
Выполнив расчёты, получим:

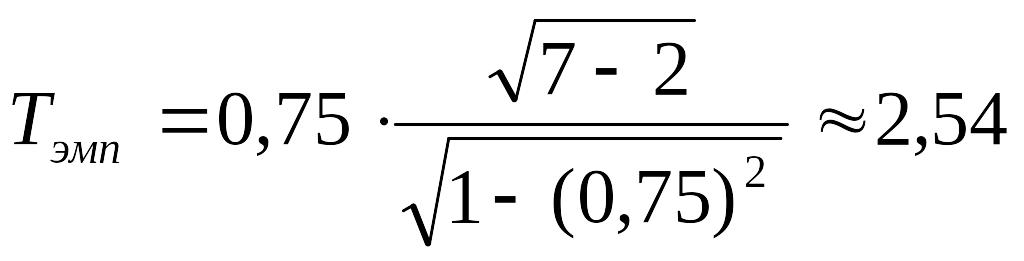
Поскольку T_эмп≈2,54<2.57≈t_кр(0,05;5), то принимается гипотеза H₀, т.е. можно говорить о несущественности связи на уровне значимости 0.05. В этом случае можно понизить уровень значимости до

t_кр(0,1; 5) 2.02 и T_эмп≈2,54>2,02=t_кр(0,1;5)

Следовательно, гипотеза H₀ на уровне значимости α=0,1 отвергается, и связь можно считать существенной.

Существенность коэффициента конкордации

Существенность коэффициента конкордации определяется по χ²- критерию. С этой целью вычисляем χ²_эмп по формуле:

Эмпирическое значение χ²_эмп сравнивается с табличным, соответствующим принятому уровню значимости α и числу степеней свободы k=n-1.

Если χ²_эмп> χ²_кр(α;k), то коэффициент конкордации W существенен на выбранном уровне значимости.

Обратимся к ранее рассмотренному примеру, где определялась множественная связь между оценками, полученными на ЕГЭ в районах Ярославской области:

	Русский язык (1)		Математика (2)		Физика (3)		История (4)		Ri	Ri2
	балл	ранг	балл	ранг	балл	ранг	балл	ранг
Ярославль	54.90	2	51.89	2	54.75	1	53.74	3	8	64
Переславль	54.93	1	50.66	3	48.59	6	53.13	4	14	196
Ростов	52.38	4	50.19	4	53.71	2	56.74	1	11	121
Рыбинск	53.06	3	52.14	1	51.55	4	52.92	5	13	169
Тутаев	50.20	6	49.30	5	49.63	5	56.33	2	18	324
Углич	50.80	5	45.43	7	47.67	7	51.14	6	25	625
Ярославский район	49.34	7	48.37	6	53.36	3	39.81	7	23	529

Было показано, что w≈0,52, S=236, m=4 (количество предметов), n=7 (количество районов).

Тогда На уровне значимости α=0,05 χ²_кр(0,05;6)=12,6.

χ²_эмп=12,64>12,6= χ²_кр, следовательно, на выбранном уровне значимости полученный коэффициент конкордации значим, и имеет место связь средней силы.

В заключении предоставим читателям опорную таблицу изложенных в пособии основных вероятностно-статистических знаний и возможных умений и навыков.

68