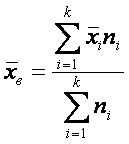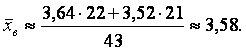- •Структура педагогического эксперимента
- •Математическая обработка педагогического эксперимента
- •Характеристики рассеивания
- •Корреляционное отношение
- •Коэффициент вариации
- •Доверительный интервал
- •Ранговые корреляции и взаимосвязи в педагогических экспериментах
- •Коэффициент корреляции Пирсона
- •Корреляционные матрицы и графы
- •Коэффициент конкордации
- •Статистические гипотезы
- •Критерий Крамера-Уэлча
- •Критерий Фишера
- •Проверка нормальности распределения
- •Критерий Фридмана
- •Критерий Пейджа
- •Значимость коэффициента корреляции
- •Существенность коэффициента конкордации
СОДЕРЖАНИЕ
Введение
Структура педагогического эксперимента
Математическая обработка педагогического эксперимента
Характеристики положения вариационного ряда
Характеристики рассеивания
Корреляционное отношение
Коэффициент вариации
Доверительный интервал
Ранговые корреляции и взаимосвязи в педагогических экспериментах
Коэффициент корреляции Пирсона
Корреляционные матрицы и графы
Коэффициент конкордации
Критерий Стьюдента
Критерий Крамера-Уэлча
Критерий Фишера
Критерий Пирсона
Проверка нормальности распределения
Критерий Манна-Уитни
Критерий Колмогорова-Смирнова
Критерий Колмогорова-Смирнова
Критерий знаков
Критерий Крускала-Уоллиса
Критерий Фридмана
Критерий Пейджа
Значимость коэффициента корреляции
Существенность коэффициента конкордации
Отзыв о пособии
Пособие предназначено для студентов и аспирантов педагогических высших учебных заведений. В книге приведены основные сведения о вероятностно-статистических методах исследования, позволяющие проводить анализ и планирование педагогических наблюдений и экспериментов. Помимо теоретических сведений пособие содержит массу показательных примеров, наглядно иллюстрирующих практическое применение математической статистики в педагогике и психологии.
Пособие содержит множество взаимодополняющих методов, что позволяет исследователю более полно и точно обосновать результаты проводимого им эксперимента.
Пособие будет полезно не только студентам и аспирантам, но и учителям средних общеобразовательных школ, поскольку содержит актуальные в условиях современного образования педагогические приемы, позволяющие преподавателю математически обосновать результаты своей экспериментальной и повседневной педагогической деятельности.
Пособие не перегружено математическими терминами, написано в доступной форме, почему может быть рекомендовано не только студентам и преподавателям математических специальностей, но и учителям гуманитарного цикла.
Учебное пособие может быть полезно для проведения курсов повышения квалификации учителей, а также для самостоятельной работы аспирантов в области статистической и математически обоснованной обработки результатов своих научных исследований.
Следует отметить, что пособие содержит интересный подход в иллюстрации применения статистических критериев. Проверку статистических гипотез предлагается проводить с использованием наглядных циклических схем, упрощающих восприятие алгоритма проверки и способствующих лучшему запоминанию предлагаемого материала.
Математический материал в пособии представлен последовательно, в порядке усложнения. Благодаря такой системе изложения, проиллюстрированной большим числом подробно рассмотренных примеров прикладного характера, обеспечивается легкость и доступность восприятия, что является несомненным достоинством книги.
Пособие дополняет достаточно большой объем литературы, посвященной вероятностно-статистическим методам исследования. При этом книга рассчитана на исследования в области педагогики и психологии, что выделяет ее из массы учебных материалов, посвященных данной теме.
Введение
Для педагога очень важно уметь анализировать результаты своей профессиональной деятельности, а также грамотно планировать и проводить психолого-педагогические эксперименты, обрабатывать их результаты.
Специфика статистической обработки результатов психолого-педагогических исследований заключается в том, что анализируемая база данных характеризуется большим количеством показателей различных типов, их высокой вариативностью под влиянием неконтролируемых случайных явлений, необходимостью учета объективных и субъективных факторов, сложностью корреляционных связей между переменными выборками.
Психолого-педагогические исследования можно разбить на три группы. Первая – это номинальные переменные (пол, возраст и другие анкетные данные). Арифметические операции над такими величинами лишены смысла, так что результаты описательной статистики (выборочные средние, дисперсия) к таким величинам не применимы. Классический способ их анализа – разбиение на классы относительно тех или иных номинальных признаков и проверка значимых различий по классам. Вторая группа данных имеет количественную шкалу измерения, но эта шкала является порядковой (ординальной). При анализе ординальных переменных используются как разбиение на подвыборки, так и ранговые технологии (например, нахождение ранговой корреляции). Третья группа – количественные переменные, отражающие степень выраженности замеряемого показателя, – это успеваемость, тесты Амтхауэра, Кеттелла и другие оценочные тесты. При работе с выборками этой группы применимы все стандартные виды анализа, и при достаточно большом объеме выборки их распределение обычно близко к нормальному.
Одной из главных целей исследования является анализ измерений, происходящих в процессе обучения, оценка значимости и направленности этих изменений и выявление основных факторов, влияющих на процесс. При этом возможны два подхода. Можно рассматривать длительность эксперимента и вычислять его корреляцию с интересующими нас индивидуальными характеристиками испытуемого. Однако, проводимые исследования показывают, что в процессе профессионализации изменяются зачастую не сами показатели, а структура взаимосвязей между ними. Поэтому более предпочтительным методом является разбиение данных на группы (подвыборки), их самостоятельный, а затем сравнительный анализ и проверка значимости различий в группах Для аргументации эффективности того или иного подхода в педагогике, как правило, проводят формирующий эксперимент.
Структура педагогического эксперимента
Педагогический эксперимент, или формирующий эксперимент, — это специфический исключительно для педагогики вид эксперимента, в котором активное воздействие экспериментальной ситуации на испытуемого должно способствовать его развитию и личностному росту.
Педагогический эксперимент требует очень высокой квалификации со стороны экспериментатора, так как неудачное и некорректное использование методик может привести к негативным для испытуемого последствиям.
В ходе такого эксперимента предполагается формирование определенного качества (именно поэтому он еще называется "формирующий"). Можно выделить множество различных педагогических экспериментов. Однако, большинство из них имеют общую структуру. Как правило, в эксперименте участвуют две группы: экспериментальная и контрольная. Необходимо, чтобы до проведения эксперимента обе группы несущественно отличались по исследуемому признаку. Участникам экспериментальной группы предлагается новый метод обучения (воспитания) или определенное задание, которое (по мнению экспериментаторов) будет способствовать формированию заданного качества. Контрольной группе испытуемых данное задание не предоставляется и обучение ведется традиционным способом. В конце эксперимента две группы снова сравниваются между собой для оценки полученных результатов.
Важно не только зафиксировать и сравнить полученные результаты, но и обосновать их, доказать неслучайность и значимость полученных различий. Как правило, установить связь между воздействием на испытуемого и полученным результатом, а также обосновать эффективность (или неэффективность) проведенного эксперимента помогают инструменты математической статистики.
Формирующий эксперимент как метод появился благодаря теории деятельности (А.Н. Леонтьев, Д.Б.Эльконин и др.), в которой утверждается идея о первичности деятельности по отношению к психическому развитию. В ходе формирующего эксперимента активные действия совершают как испытуемые, так и экспериментатор. Со стороны экспериментатора необходима высокая степень контроля над протекающим экспериментом и своевременное внесение корректировок в данный процесс. Это отличает эксперимент от наблюдения или экспертизы. В эксперименте желательна фиксация числовых результатов в контрольной и экспериментальной группах с целью последующей проверки данных вероятностно-статистическими методами обработки.
Математическая обработка педагогического эксперимента
Большинство педагогических исследований призвано ответить на вопрос, верно ли сделанное исследователем предположение, подтверждается ли выдвинутая им гипотеза. Наиболее привлекательным с точки зрения эффективности и целесообразности методом психолого-педагогического исследования является опыт. Однако, сами результаты опыта, как правило, не позволяют нам сделать чётких и научно обоснованных выводов о справедливости (или ложности) выдвинутой гипотезы. Проанализировать результаты опыта и сделать полезные выводы помогают математические методы исследования.
Очевидно, что в большинстве случаев невозможно поставить опыт над всем множеством объектов, в отношении которых формулируется исследовательская гипотеза. Такое множество носит название генеральной совокупности. Например, при желании понять, каким образом меняется успеваемость учащихся при использовании той или иной модели обучения, исследователь должен был бы провести эксперимент с каждым учеником. Но такой метод затруднителен в силу его трудоёмкости, дороговизны и длительности. Поэтому педагогические и психологические опыты, как правило, производятся не над всей генеральной совокупностью исследуемых объектов, а лишь над их частью, называемой выборкой. Таким образом, эксперимент, а затем и анализ полученных результатов осуществляется над выборкой.
Для корректного исследования необходимо, чтобы изучаемая выборка в максимальной мере соответствовала генеральной совокупности, отражала наблюдаемые в ней явления, их изменчивость, т.е. была репрезентативной. Наиболее простой способ добиться репрезентативности – это составить выборку методом случайного отбора исследуемых объектов. Данный метод предполагает соблюдение таких условий, при которых каждый член генеральной совокупности имеет равные с другими шансы попасть в выборку. Наличие какой-либо закономерности отбора не допускается.
Результаты исследования репрезентативной выборки можно подвергать анализу с использованием математических методов. Для этого необходимо специальное оформление (представление) результатов опыта. Наиболее востребованным и часто применяемым является метод представления результатов опыта в виде вариационного ряда.
Вариационный ряд – это таблица, отображающая зависимость между видами исходов проводимого опыта и количествами тех или иных исходов.
Рассмотрим следующий эксперимент. Тридцати студентам был задан следующий вопрос: «Какое чувство наиболее ярко проявляется (ощущается) Вами в момент сдачи важного экзамена?» В результате вопроса были получены такие варианты ответов: «страх», «подавленность», «волнение», «растерянность», «ничего не чувствую», «эмоциональное возбуждение». Т.е. в данном эксперименте опытом является опрос. Разновидности исхода опыта – это различные ответы испытуемых. Чтобы составить вариационный ряд, необходимо знать, сколько человек дали тот или иной ответ. Если «страх» испытывают 5 человек, «подавленность» - 2 человека, «волнение» - 14 человек, «растерянность» - 4 человека, «ничего не чувствуют» - 2 человека, а «эмоциональную возбуждение» - 3 человека, то искомая таблица будет выглядеть следующим образом:
Исход опыта |
Страх |
Подавленность |
Волнение |
Растерянность |
Ничего не чувствуют |
Эмоциональное возбуждение |
Количество исходов |
5 |
2 |
14 |
4 |
2 |
3 |
Построенная таблица отражает результаты проделанного опыта. При этом для математической обработки результата, как правило, необходимо представить исходы опыта в числовом виде. Например, испытываемые чувства можно пронумеровать и в таблице вместо их словесной формулировки записать соответствующие номера.
В диссертационной работе Л.А. Агафоновой рассматривается выбор учащихся курсов УПК. Из 52 человек курсы технической направленности выбрали 27 человек, «журналистику» - 11 человек, «воспитатель» - 7 человек и «правоведение» - 7 человек.
Построим для данной выборки школьников вариационный ряд, пронумеровав курсы. В результате получим следующую таблицу:
-
Курсы
1
2
3
4
Выбрало человек
27
11
7
7
В некоторых исследованиях исходы опыта выражаются числами, а значит, искусственное числовое представление вариантов не требуется.
В классе провели тестирование по определению уровня доверия учащихся друг к другу. Уровень доверия определяется по 10-балльной шкале. Результатом исследования стали следующие данные: уровень доверия, равный 1, определился у 1 человека, равный 2 – у 3 человек, равный 4 – у 6 человек, равный 6 – у 9 человек, равный 8 – у 4 человек, равный 10 – у 2 человек.
Запишем полученные результаты в виде вариационного ряда, где имеют место следующие варианты: 1, 2, 4, 6, 8 и 10 баллов. Получим следующую таблицу:
Вариант |
1 |
2 |
4 |
6 |
8 |
10 |
Количество испытуемых |
1 |
3 |
6 |
9 |
4 |
2 |
Для удобства при использовании математических методов исследования элементы множества значений выборки (варианты исхода опыта) обозначают через xi. В рассматриваемом примере их можно обозначить: x1=1, x2=2, x3=4, x4=6, x5=8, x6=10. Количества испытуемых, соответствующих тому или иному варианту, называют частотами данных вариантов. Обычно частоты обозначаются через mi. Например, для варианта x3=4 частота m3 равна 6. При этом общее количество испытуемых, принявших участие в исследовании, называется объёмом выборки, который находится как сумма всех частот и обозначается буквой n. В данном случае n=1+3+6+9+4+2=25.
Для того чтобы показать, какую долю от всего объёма выборки представляет тот или иной вариант, используется понятие относительной частоты.
Относительные
частоты обозначаются через fi
и определяются как отношение соответствующей
частоты mi
к объёму выборки n,
т.е.
 .
Таблица, отображающая зависимость между
вариантами xi
и относительными частотами fi
называется статистическим
рядом.
.
Таблица, отображающая зависимость между
вариантами xi
и относительными частотами fi
называется статистическим
рядом.
Важно
заметить, что в вариационном и
статистическом рядах варианты принято
располагать в порядке возрастания.
Сумма относительных частот статистического
ряда всегда равна единице:
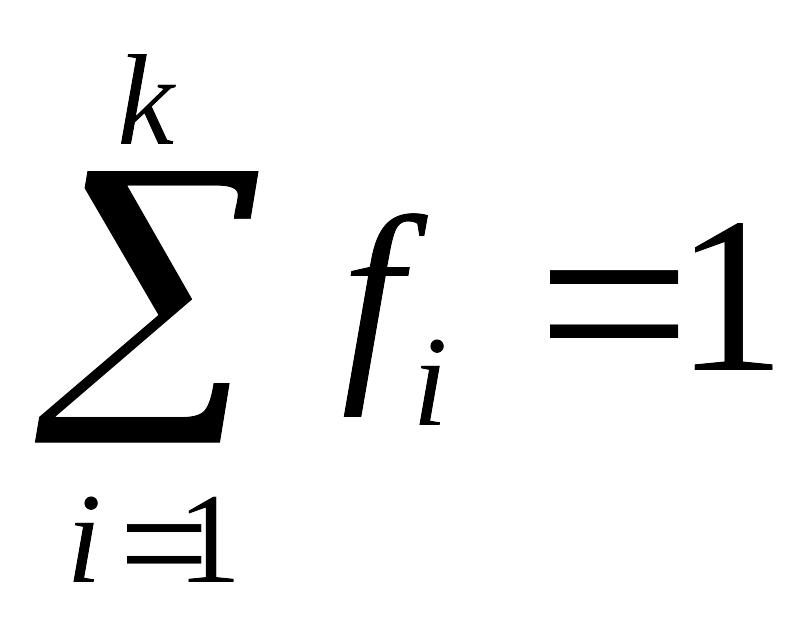 ,
где k
– количество различных вариантов.
,
где k
– количество различных вариантов.
Составим статистический ряд для рассмотренного опыта с изучением уровня доверия школьников друг к другу.
Для
решения поставленной задачи достаточно
разделить соответствующие значения
частот на объём выборки n=25.
Например,
![]() и т.д. В результате получим следующий
статистический ряд:
и т.д. В результате получим следующий
статистический ряд:
Вариант xi |
1 |
2 |
4 |
6 |
8 |
10 |
Относительная частота fi |
0.04 |
0.12 |
0.24 |
0.36 |
0.16 |
0.08 |
Убедимся,
что
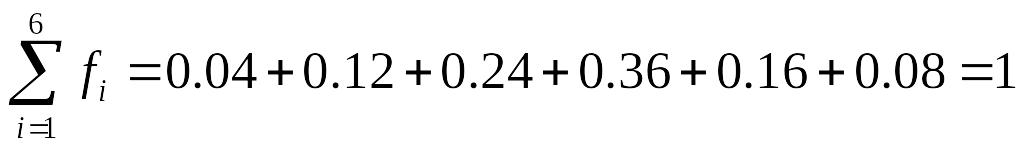 .
.
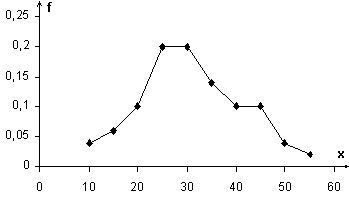
Иногда для лучшей иллюстрации результатов исследования используют полигон частот.
Под полигоном частот выборки понимают ломаную линию с вершинами в точках (xi; mi). Используют также полигон относительных частот выборки, для которого вершины ломаной имеют координаты (xi; fi).
Построим полигон относительных частот для изучения уровня тревожности (по 100-балльной шкале), которое дало следующие результаты:
xi (Тревожность, баллы) |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
mi (Количество испытуемых, чел.) |
2 |
3 |
5 |
10 |
10 |
7 |
5 |
5 |
2 |
1 |
Найдём сначала объём выборки: n=2+3+5+10+10+7+5+5+2+1=50. Далее построим статистический ряд. Для этого найдём относительные частоты .
xi (Тревожность) |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
fi (Относительная частота) |
0.04 |
0.06 |
0.1 |
0.2 |
0.2 |
0.14 |
0.1 |
0.1 |
0.04 |
0.02 |
Теперь можно построить полигон относительных частот.
Помимо полигона частот для иллюстрации результатов опыта используются также столбчатые и круговые диаграммы.
Столбчатая диаграмма строится аналогично полигону частот. Отличие заключается в том, что вместо отрезков изображаются прямоугольники соответствующей высоты.
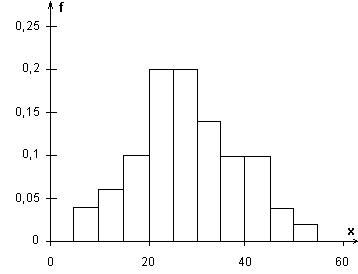
На
круговой диаграмме вариант отображается
в виде сектора, градусная мера угла
которого равна
![]() .
Рассчитаем градусные меры секторов,
соответствующих тем или иным частотам:
.
Рассчитаем градусные меры секторов,
соответствующих тем или иным частотам:
Xi (Тревожность) |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
fi (Относительная частота) |
0.04 |
0.06 |
0.1 |
0.2 |
0.2 |
0.14 |
0.1 |
0.1 |
0.04 |
0.02 |
Градусная мера сектора |
14.4 |
21.6 |
36 |
72 |
72 |
50.4 |
36 |
36 |
14.4 |
7.2 |
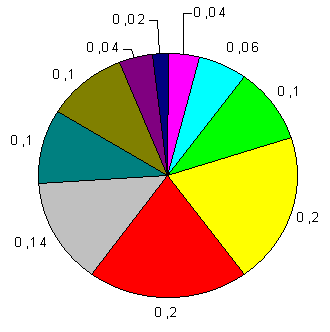
Таким образом, круговая диаграмма будет иметь вид:
Помимо диаграмм для наглядного представления результатов, а также для установления аналога с классическим законом распределения, используется гистограмма, для чего вводится понятие плотности относительной частоты.
Плотность
относительной частоты равна отношению
суммы частот соответствующего интервала
к произведению общего объёма выборки
n
и длины hi
соответствующего интервала. Т.е. плотность
относительной частоты вычисляется
следующим образом:
![]() .
.
Пусть результаты теста записаны в таблице:
Результат теста (в баллах) (интервалы) |
Количество испытуемых (чел.), mi |
Плотность относительной частоты |
Менее 3 баллов |
2 |
|
От 3 до 4 баллов |
8 |
|
От 4 до 5 баллов |
15 |
|
От 5 до 6 баллов |
5 |
|
Построим гистограмму результатов тестирования, для чего потребуется нахождение плотности относительной частоты. Она рассчитывается следующим образом. Сначала необходимо узнать объём n всей выборки, т.е. количество участников тестирования.
n=2+8+15+5=30.
Для каждого интервала находим его длину hi:
h1=3-0=3, h2=4-3=1, h3=5-4=1, h4=6-5=1.
Для построения гистограммы выборки воспользуемся прямоугольной декартовой системой координат. По оси абсцисс отметим имеющиеся интервалы: от 0 до 3, от 3 до 4, от 4до 5 и от 5 до 6. Сопоставим каждой абсциссе из выбранного интервала ординату, равную соответствующей плотности относительной частоты (см. рисунок). В качестве графика получим отрезки, параллельные оси абсцисс. Для наглядности эти отрезки можно достроить до закрашенных прямоугольников. При этом площадь каждого полученного прямоугольника будет численно равна соответствующей относительной частоте. Поэтому вся площадь закрашенной фигуры будет равна единице. Таким образом, мы получим графическое отображение относительных частот выборки.
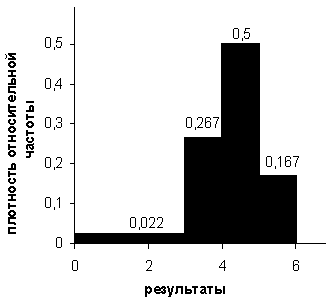
При построении гистограммы мы опирались на данные, записанные в таблице с помощью интервального метода. Если выборка имеет сравнительно большой объём или содержит большое количество различных вариантов, то могут возникнуть трудности вычислительного характера. Для решения этой проблемы и применяется метод интервалов.
Суть метода интервалов заключается в разбиении множества значений измеряемой величины на интервалы. Тогда выборка записывается следующим образом:
Измеряемая величина xi |
|
|
… |
Частота mi |
m1 |
m2 |
… |
Такая
запись означает, что выборка содержит
m1
значений величины xi
таких, что
![]() ,
m2
значений величины xi
таких, что
,
m2
значений величины xi
таких, что
![]() .
Выборку можно представить в виде любого
количества интервалов.
.
Выборку можно представить в виде любого
количества интервалов.
Подытоживая сказанное, заметим, что для организации педагогических исследований с помощью математических методов изначально полученную в результате опыта информацию необходимо представить в виде вариационного или статистического ряда. Для наглядности вариационный и статистический ряды изображаются при помощи диаграмм, полигонов частот или гистограмм.
Зная, как можно представить результаты эксперимента для их математической обработки, целесообразно перейти непосредственно к рассмотрению математических методов.
Характеристики положения вариационного ряда Одной из задач педагогического исследования является сравнение полученных результатов. Например, после проведения контрольной работы в параллельных классах мы хотим узнать, какой класс справился лучше. Таким образом, возникает необходимость сравнения данных из нескольких вариационных (или статистических) рядов. После написания срезовой контрольной работы по математике ученики двух десятых классов одной школы показали следующие результаты:
Ученики какого класса справились с контрольной работой лучше? С этой целью охарактеризуем результаты испытания в каждом классе одним числом. В математической статистике существует понятие выборочной средней величины. Пусть выборка задана своим вариационным рядом:
Тогда выборочной средней будет называться величина, определяемая по формуле:
где
n
– объём выборки, т.е.:
Воспользовавшись предложенной формулой, найдём выборочные средние для двух классов.
Для
10 «А» класса:
Для
10 «Б» класса:
Заметим, что выборочная средняя величина в данной задаче показывает среднюю оценку десятиклассников. Тогда, согласно проделанным расчётам, можно сказать, что в 10 «А» классе средняя оценка, полученная за контрольную работу, выше, чем в 10 «Б» классе. Поэтому можно сделать вывод, что 10 «А» класс справился с данной контрольной работой лучше. При этом следует иметь в виду, что учащиеся обоих классов писали одну и ту же контрольную работу, и проверял данную работу один учитель. В противном случае, если задания контрольных работ в различных классах были бы разными или они оценивались различными педагогами, сделанный вывод о том, какой класс справился с работой лучше, был бы некорректным. Помимо выборочной средней охарактеризовать успеваемость помогает такое понятие как медиана. Под медианой выборки понимают такое значение Me измеряемой величины, которое разбивает выборку на две группы такие, что суммы относительных частот в первой и во второй группах должны быть не менее ½. Составим таблицу с относительными частотами для 10 «А».
Таким образом, в рассмотренном примере для 10 «А» класса медианой является оценка «4», т.к. 10 «А» можно разделить на 2 группы, причем суммы относительных частот в группах будут равны:
Аналогичным образом 10 «Б» можно разбить на 2 группы (10 и 11 человек). В данном случае в роли числа M также выступает число 4, т.к.
Выборка может иметь одну либо две медианы. Например, по предложенной ниже таблице можно заметить, что выборка имеет медианы M1=3 и M2=4.
Число 3 является медианой, т.к.
Однако, число 4 также является медианой, потому что:
Заметим, что некоторые авторы считают невозможным наличие двух медиан и предлагают в подобном случае выбрать в качестве медианы среднее арифметическое двух медиан. В качестве дополнительной характеристики выборки медиану рекомендуется использовать в тех случаях, когда выборка содержит варианты, сильно отличающиеся от выборочного среднего. Кроме медианы можно использовать такую числовую характеристику, как мода. Мода показывает, какой вариант встречается в выборке наиболее часто. В рассмотренном ранее примере для 10 «А» класса модой является оценка «4», т.к. она имеет самую большую частоту в предложенной выборке. Вернемся к примеру с контрольной работой. По имеющимся данным можно найти средний балл за проведённую контрольную работу для обоих классов. Сделать это можно несколькими способами. Способ первый. Обобщить имеющиеся данные в виде одного вариационного ряда. Для этого рассчитаем, сколько десятиклассников в двух классах написали контрольную работу на «2», на «3», на «4» и на «5» и запишем данные в таблицу.
Далее воспользуемся формулой для выборочной средней. При этом учтём, что объём n полученной выборки будет равен 43. Тогда выборочная средняя для двух классов школы будет равна:
Таким образом, средний балл за контрольную работу в обоих классах получился выше, чем в «Б» классе и ниже, чем в «А» классе. Способ второй.
Если
выборку можно разбить на несколько
групп (например, на разные школы, классы
и т.д.), то выборочная средняя
Известно,
что общая выборочная средняя (
Средний
балл для обеих групп нам уже известен:
для первой группы он равен
Заметим, что решение задачи обоими способами привело нас к одному результату. Рассмотрим аналогичный пример. Проведение ЕГЭ по математике в трёх школах дало следующие результаты по 100-балльной шкале:
Определим средний результат по ЕГЭ для трёх данных школ. В предложенной задаче общий объём n выборки – это количество учеников, сдававших ЕГЭ, n=155. Средний балл для каждой школы можно считать групповой средней, где в роли i-ой группы выступает соответствующая школа.
Тогда решение
задачи сводится к вычислению общей
средней через групповые средние по
указанной выше формуле.
Попытаемся определить, как сильно отличаются друг от друга средние результаты по ЕГЭ в трёх школах. Для этого в математической статистике существуют показатели рассеивания. |

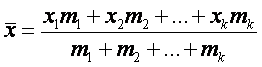 ,
или
,
или
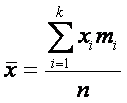 ,
,
 .
.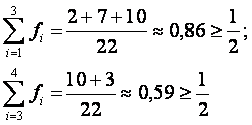
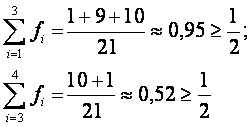


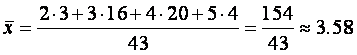 .
.