Тема: параметрические критерии различий

t-критерий Стьюдента

1. Случай несвязных выборок

Критерий t Стьюдента направлен на оценку различий величин средних двух выборок Х и Y, которые распределены по нормальному закону.

Критерий может быть использован для выборок не равных по численности.

Формула (6) позволяет рассчитать t-критерий Стьюдента для равных по численности выборок, т.е. n₁ = n₂ = n

= (6)

В случае неравночисленных выборок, т.е. когда n₁ ≠ n₂, то рассчитывать t-критерий Стьюдента нужно по формуле 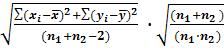(7).

= (7)

Критические значения t-критерий Стьюдента находим по таблице.

2. Случай связных выборок

В случае связных выборок с равным числом измерений в каждой можно использовать формулу (8).

(8)

В свою очередь рассчитывается по формуле 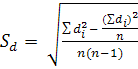(9).

(9)

F-критерий Фишера

Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух рядов наблюдений. Критерий Фишера рассчитывается по формуле (10). При вычислении критерия Фишера нужно помнить о том, что величина числителя должна всегда быть больше величины знаменателя.

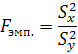
где

Пример. Психолог провел тестирование учащихся 4-х классов по методике ТУРМШ. Психолог хочет проверить различаются средние величины выборок и есть ли различия в степени однородности показателей умственного развития между классами. Полученные результаты представлены в таблице.

№ п/п	4-А	4-Б	№ п/п	4-А	4-Б
1	90	41	6	53	65
2	29	49	7	34	63
3	39	56	8	40	87
4	79	64	9	75	77
5	88	72	10	79	62
суммы				606	636
средние				60,6	63,6

Решение представим в табличной форме.

1. Используя t-критерий Стьюдента сравним значения средних величин показателей умственного развития учащихся 4-х классов.

№	Классы		Отклонение от среднего		Квадраты отклонений
	4-А (хi)	4-Б (yi)
1	90	41	90-60,6=29,4	41-63,6=-22,6	864,36	510,76
2	29	49	29-60,6=-31,6	49-63,6=-14,6	998,56	213,16
3	39	56	39-60,6=-24,6	56-63,6=-7,6	605,16	57,76
4	79	64	79-60,6=18,4	64-63,6=0,4	338,56	0,16
5	88	72	88-60,6=27,4	72-63,6=8,4	750,76	70,56
6	53	65	53-60,6=-7,6	65-63,6=1,4	57,76	1,96
7	34	63	34-60,6=-26,6	63-63,6=-0,6	707,56	0,36
8	40	87	40-60,6=-20,6	87-63,6=23,4	424,36	547,56
9	75	77	75-60,6=14,4	77-63,6=13,4	207,36	179,56
10	79	62	79-60,6=18,4	62-63,6=-1,6	338,56	2,56
Сумма	606	636			5293	1584,4
среднее	60,6	63,6

= 8,74

2. Число степеней свободы к=10+10-2=18

По таблице критических значений для данного числа степеней свободы находим

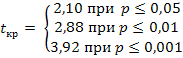
Зона незначимости Зона значимости

3,43

2,1 2,88 3,92

3. Полученное значение 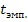попало в зону значимости на уровне 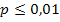. Из этого следует, что величины средних двух выборок значимо различаются. В терминах статистических гипотез вывод звучит следующим образом: нулевая гипотеза (об отсутствии различий) отклоняется, а принимается альтернативная гипотеза (о наличии различий).

Таким образом, средние величины показателей умственного развития по методике ТУРМШ у учащихся 4-х классов значимо различаются.

4. Используя F критерий Фишера, проверим, есть ли различия в степени однородности показателей умственного развития между классами.

По таблице критических значений для F критерия при степенях свободы к=10-1=9 находим F_кр.

Строим ось значимости:

Зона незначимости Зона неопределенности Зона значимости

0,05 0,01

3,18 3,34 5,35

Полученная величина F критерия Фишера попала в зону неопределенности, а это значит, что на уровне 5% мы принимаем альтернативную гипотезу о наличии различий. Психолог может утверждать, что по степени однородности такого показателя, как умственное развитие, имеется различие между выборками из двух классов.