
- •Вопросы на 3 балла по курсу математического анализа
- •Преподаватель: е.П. Бокмельдер
- •Вопросы на 4 балла по курсу математического анализа
- •Преподаватель: е.П. Бокмельдер
- •Упражнения
- •Контрольная работа по рядам и интегралам Фурье.
- •Интегралы, зависящие от параметра
- •Упражнения
- •Контрольная работа по теме «Интегралы, зависящие от параметра»
- •Кратные, криволинейные и поверхностные интегралы
- •Задачи Контрольная работа по теме: «Двойные интегралы»
- •Вариант 1
- •9. Найти если
- •Вариант 2
- •5. Вычислить работу силового поля вдоль дуги
- •9. Найти если .
- •Мера и интеграл Лебега
- •-Кольцо измеримых множеств и счетная аддитивность внешней меры на нем.
- •Упражнения
- •-Функция:
- •- Функция:
- •Примеры
Задачи Контрольная работа по теме: «Двойные интегралы»
Поменять порядок интегрирования в повторном интеграле
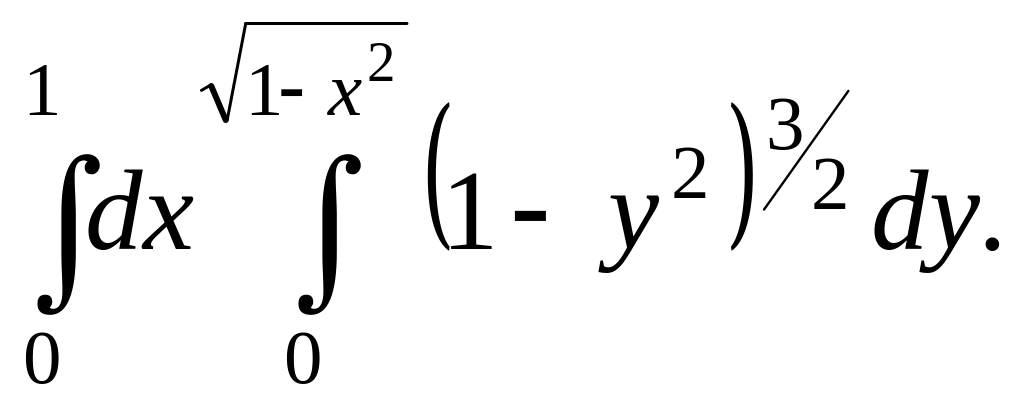
Вычислить
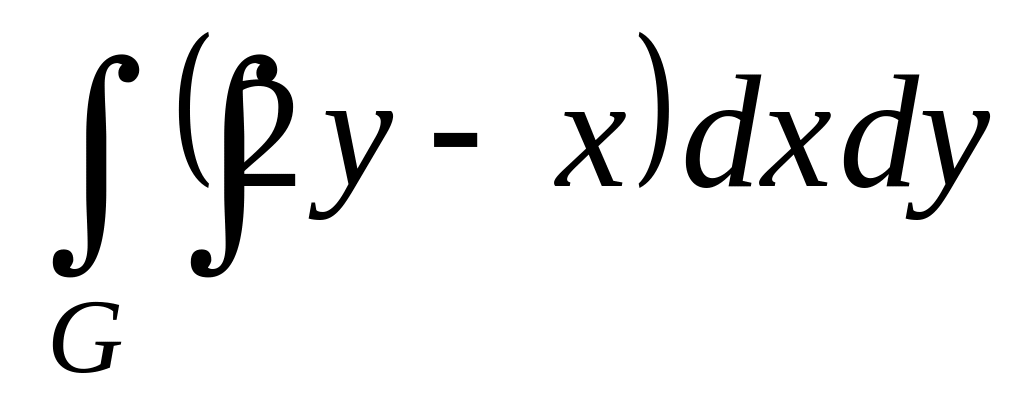 ,
где
,
где

Вычислить
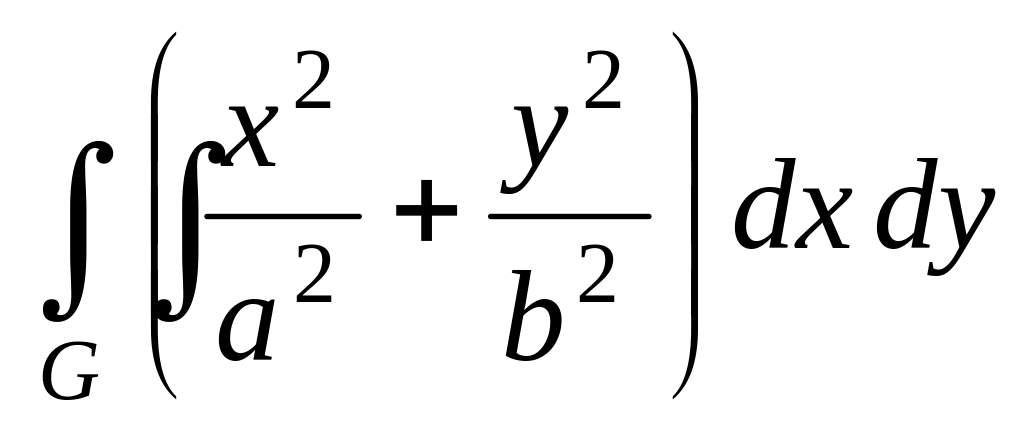 ,
где
,
где
 ограничено линиями
ограничено линиями
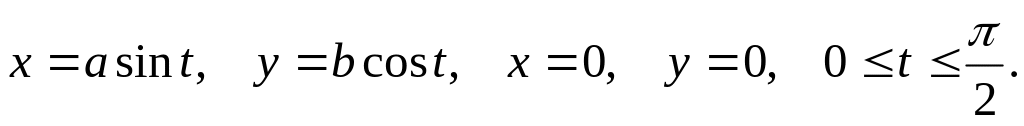
Найти объем тела, ограниченного поверхностями
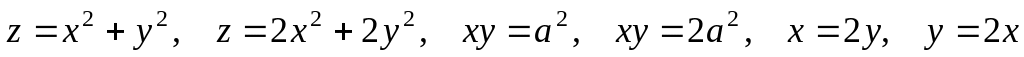

Контрольная работа по теме: «Теория поля», 4 семестр, прикладники.
Вариант 1
1. В каких точках пространства градиент
поля
![]() перпендикулярен оси
перпендикулярен оси
![]() ?
?
2. Найти векторные линии поля
![]()
3. Найти массу части эллипса
![]() расположенной в первой четверти, если
ее плотность
расположенной в первой четверти, если
ее плотность
![]()
4. Найти площадь бок. поверхности цилиндра
![]() ограниченной плоскостями
ограниченной плоскостями
![]()
5. Вычислить работу силового поля
![]() вдоль дуги
вдоль дуги
![]()
6. Найти поток вектора
![]() через верхнюю часть поверхности
параболоида
через верхнюю часть поверхности
параболоида
![]()
7. С помощью формулы Остроградского
найти поток вектора
![]() через внешнюю сторону поверхности
симплекса
через внешнюю сторону поверхности
симплекса
![]()
8. С помощью формулы Грина найти циркуляцию
вектора
![]() вдоль эллипса
вдоль эллипса
![]() против часовой стрелки.
против часовой стрелки.
9. Найти если
10. Проверить потенциальность и найти
потенциал поля
![]()
Вариант 2
1. Найти производную функции
![]() в точке
в точке
![]() по направлению прямой
по направлению прямой
![]() в сторону возрастания поля.
в сторону возрастания поля.
2. Убедиться в ортогональности линий
уровня скалярных полей
![]()
3. Найти массу дуги конической винтовой
линии
![]() от точки
от точки
![]() до точки
до точки
![]() если ее плотность
если ее плотность
![]()
![]() .
.
4. Определить суммарный электрический
заряд, распределенный на части поверхности
параболоида
![]() вырезаемой из него цилиндром
вырезаемой из него цилиндром
![]() если плотность заряда
если плотность заряда
![]()
5. Вычислить работу силового поля вдоль дуги
6. Найти поток вектора
![]() через поверхность параболоида
через поверхность параболоида
![]()
вырезаемую цилиндром
![]() ориентированную
в соответствии с направлением орта
ориентированную
в соответствии с направлением орта
![]()
7. С помощью формулы Остроградского
найти поток вектора
![]() через всю поверхность куба
через всю поверхность куба
![]() в направлении внешней нормали.
в направлении внешней нормали.
8. С помощью формулы Стокса найти
циркуляцию вектора
![]() по сечению сферы
по сечению сферы
![]() плоскостью
плоскостью
![]() в положительном направлении относительно
орта
в положительном направлении относительно
орта
![]()
9. Найти если .
10. Проверить соленоидальность поля

Мера и интеграл Лебега
Внешняя мера Лебега и ее свойства.
-Кольцо измеримых множеств и счетная аддитивность внешней меры на нем.
Классы измеримых множеств в : открытые, замкнутые, борелевские множества, множества меры нуль.
Измеримые функции и их свойства.
Сходимость функциональной последовательности почти всюду и теорема Егорова. Сходимость по мере, связь со сходимостью почти всюду - теорема Лебега. Сходимость по мере, связь со сходимостью почти всюду - теорема Рисса.
Простые функции. Приближение измеримой функции простыми функциями.
Интеграл Лебега и его простейшие свойства.
Свойства счетной аддитивности и абсолютной непрерывности интеграла Лебега как функции множества.
Предельный переход под знаком интеграла Лебега: теорема Леви о монотонной сходимости для последовательностей и рядов; теорема Фату; теорема Лебега об ограниченной сходимости.
Сравнение интеграла Лебега с интегралом Римана.
Пространство . Сходимость в среднем. Полнота пространства .
Пространство . Сходимость в средне-квадратичном. Связь с другими видами сходимости. Полнота пространства . Всюду плотные подмножества в и в .
