Вопросы на 3 балла по курсу математического анализа
4-ый семестр
Преподаватель: е.П. Бокмельдер
Тригонометрический ряд Фурье и формулы для вычисления коэффициентов Фурье.
1-ая и 2-ая теоремы Вейерштрасса
Определение равномерной сходимости несобственного интеграла, зависящего от параметра
Признак Вейерштрасса равномерной сходимости несобственного интеграла, зависящего от параметра
Виды
-
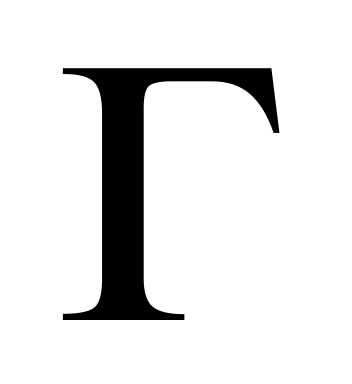и
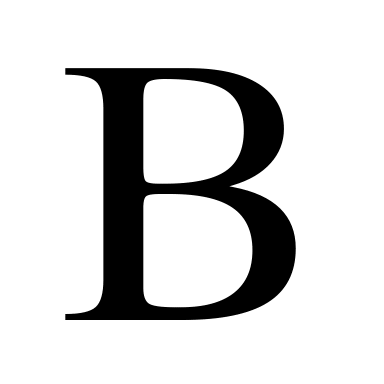-функций
и из области сходимости.Определение интеграла Римана на n-мерном параллелепипеде
Критерий Лебега интегрируемости по Риману
Формула замены переменных в кратном интеграле
Криволинейные интегралы 1-го и 2-го рода. Их физический смысл.
Поверхностные интегралы 1-го и 2-го рода. Их физический смысл.
Дивергенция векторного поля.
Ротор векторного поля.
Определения потенциального и соленоидального полей.
Запись характеристик скалярных и векторных полей с помощью вектора набла.
Определение внешней меры Лебега
Определение измеримого множества
Определение измеримой функции
Определение равномерной сходимости функциональной последовательности на множестве Е.
Определение сходимости функциональной последовательности почти всюду на множестве Е.
Определение сходимости функциональной последовательности по мере на множестве Е.
Определение простой функции
Определение интеграла Лебега на множестве Е.
Определение полного метрического пространства
Метрика в пространстве
.
Сходимость в среднем.Метрика в пространстве
.
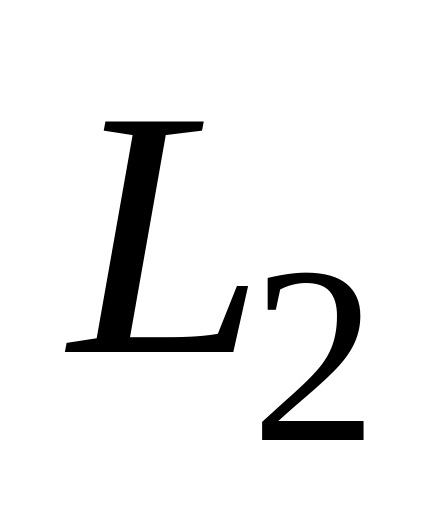Сходимость в средне-квадратичном.
Вопросы на 4 балла по курсу математического анализа
4-ый семестр
Преподаватель: е.П. Бокмельдер
Равенство Парсеваля
Достаточные условия возможности интегрирования и дифференцирования несобственного интеграла по параметру
Теорема Фубини для функции двух переменных
Приложения кратных интегралов
Формулы площади гладкой поверхности, заданной явно, неявно и параметрически.
Теорема Гаусса-Остроградского и ее физический смысл.
Теорема Стокса и ее физический смысл.
Свойства потенциального и соленоидального полей.
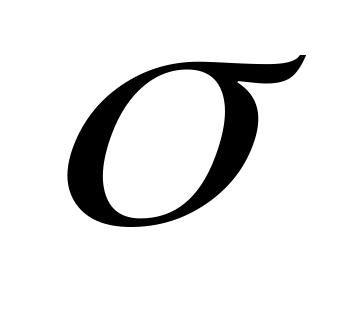-кольцо
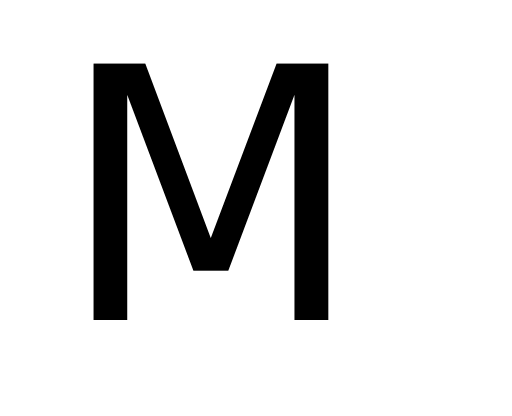измеримых множеств и счетная аддитивность
внешней меры на нем.Свойство регулярности меры Лебега в
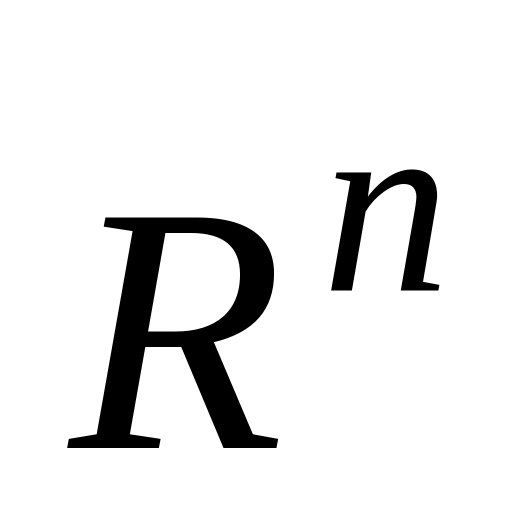.Теорема Лебега о связи между сходимостью почти всюду и сходимостью по мере.
Теорема Рисса о связи между сходимостью по мере и сходимостью почти всюду.
Предельный переход под знаком интеграла Лебега: теорема Леви о монотонной сходимости для последовательностей и рядов;
Теорема Лебега об ограниченной сходимости.
Связь между различными видами сходимости функциональной последовательности на множестве конечной меры.
Полнота пространств и . Всюду плотные подмножества в и в .
ВОПРОСЫ, УПРАЖНЕНИЯ И ЗАДАЧИ
по курсу МАТЕМАТИЧЕСКОГО АНАЛИЗА
4-ый семестр
Преподаватель: Е.П. Бокмельдер
Ряды Фурье.
Ортонормированные системы непрерывных функций на отрезке. Тригонометрическая система, ее ортогональность на отрезке длины
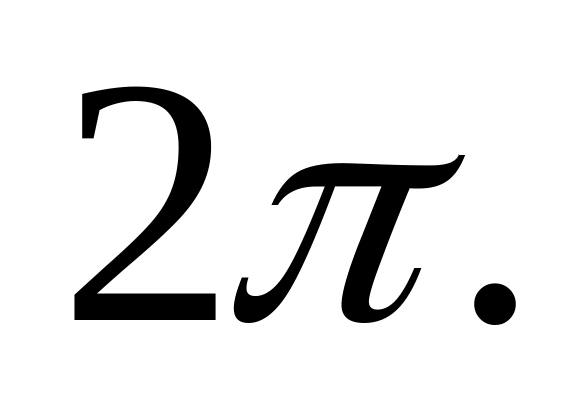Единственность разложения функции в
тригонометрический ряд.Тригонометрический ряд Фурье. Простейшие результаты о сходимости в точке. Ядра Дирихле и Фейера. Теорема Фейера и ее следствия.
Ряды Фурье по ортонормированным системам. Наилучшее приближение. Минимальное свойство коэффициентов Фурье (теорема о наилучшем среднеквадратичном приближении. Неравенство Бесселя. Стремление к нулю коэффициентов Фурье.
Ряд Фурье в интервале произвольной длины.
Равномерное приближение непрерывной функции тригонометрическими и алгебраическими многочленами. 2-ая теорема Вейерштрасса. Интеграл Фурье и его свойства.