9) Закон Малюса і його геометрична інтерпретація

10) Формули Френеля для відбивання (лише р) від діелектрика. Кут Брюстера

В рамках геометричної оптики визначається співвідношення кутів падіння, відбивання та заломлення на границі розділу прозорих середовищ з різними показниками заломлення. Фізичний розвиток даної проблеми передбачає не лише визначення співвідношення трьох кутів, але також і співвідношення амплітуд і фаз падаючого, відбитого та заломленого пучків. Якщо падаючий пучок певним чином поляризований, тобто існує певне співвідношення між p та s компонентами, то зміна співвідношення амплітуд таких компонент у відбитому та заломленому пучках, а також зміна різниці фаз між такими компонентами призведе до зміни стану поляризації, така задача була розв’язана Френелем у 1823р. для усіх кутів від до . Проблема визначення співвідношення амплітуд, фаз та станів поляризації трьох пучків може розглядатись на двох рівнях: фізичному і феноменологічному.

Фізичний розв’язок включає в себе детальний розгляд речовин, з яких складаються перше і друге середовище. Атоми і молекули на границі розділу двох середовищ розглядаються як коливні системи, які збурюються падаючим пучком і перевипромінюють світло. У такій постановці задача відбивання і заломлення розв’язана, але включає в себе надзвичайно громіздкі обчислення. Це пов’язано з тим, що кожний елементарний вторинний випромінювач занурений не лише у поле падаючого пучка, але і у поля інших вторинних випромінювачів.

Згідно феноменологічноuj підходу, прийнятому Френелем, використовується лише один параметр, а саме відносний показник заломлення двох прозорих середовищ . Оскільки в оптичному діапазоні μ ≈1, то . В основі теорії відбивання і заломлення Френеля лежить єдине припущення про поперечність світлових хвиль, яке доводиться дослідом Френеля-Араго. При розгляді відбивання і заломлення вводяться спеціальні граничні умови: як би не був поляризований падаючий пучок, його можна розкласти на тангенціальну і нормальну до границі розділу компоненти. Цей розклад відрізняється від розкладу на p і s компоненти.

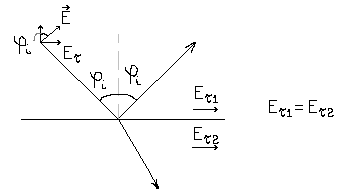
Поле у першому середовищі шукається як сума падаючого і відбитого пучків. Поле у другому середовищі складається лише із заломленого пучка.

Граничні умови:

Умова 1: По обидві сторони границі розділу тангенціальні компоненти світлового вектора повинні бути однакові, в іншому випадку виникає рух зарядів вздовж поверхні.

Умова2: За рахунок відмінності у показниках заломлення нормальна компонента зазнає стрибка.

Нехай i стосується падаючого пучка, r – відбитого, а d – заломленого.

Граничні умови для :

де ω – частоти падаючого, відбитого і заломленого пучків;

k – хвильовий вектор;

– одиничний вектор у напрямку поширення відповідного пучка так, що ;

– радіус вектор біжучої точки у першому або другому середовищі.

Для того, щоб виконувалась така гранична умова для тангенціальних компонент, необхідно щоб показники експоненти були однакові. Це означає, що t і є незалежними змінними, то одночасно повинні виконуватися наступні умови:

1)

2)

Очевидно, що умова для тангенціальної компоненти може бути визначена через кути падіння, відбивання та заломлення.

Оскільки із закону відбивання заздалегідь відомо, що то надалі можна виписувати загально φ, а . У формулах Френеля, які пов’язують між собою амплітуди і фази p і s компонент падаючого, відбитого та заломленого пучків, входять лише два кути – φ і ψ. Через співвідношення кутів падіння і заломлення у ці формулі неявно входить показник заломлення. У часткових випадках показники заломлення виписуються у явному вигляді.

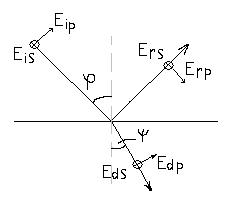
У заломленому пучку зберігається співвідношення фаз між p і s компонентами. Натомість у відбитому пучку має місце зсув фаз між цими компонентами на π, що показано зміною орієнтації .

Формули Френеля для p і s компонент мають наступний вигляд вигляд:

– перша формула Френеля.

З першої формули Френеля як частковий випадок випливає закон Брюстера, а саме наявність кута падіння, при якому відбитий пучок буде повністю лінійно поляризований і містить лише s компоненту. У формулювання закону Брюстера входить твердження про те, що повна поляризація відбитого пучка має місце, коли відбитий і заломлений пучки складають кут .

Для s-компоненти . З даної формули видно, що s компонента відбивається з ненульовою амплітудою при довільному куті падіння.

З наведених формул видно, що амплітудні коефіцієнти відбивання та заломлення завжди є дійсними, в залежності від співвідношення кутів φ та ψ ці коефіцієнти можуть бути додатні або від’ємні.

Фізичний зміст знаку «-» полягає в тому, що він визначає зсув фаз між компонентами на : . При цьому практично ніколи не виникає уявний коефіцієнт . Це означає, що якщо падаючий пучок лінійно поляризований і містить як p, так і s компоненту, то відбитий та заломлений пучки також будуть містити ці компоненти, можливо зі змінними амплітудами, при чому ці компоненти будуть або синфазними, або протифазними. Тому і відбитий, і заломлені пучки також будуть лінійно поляризовані. Тобто при звичайному відбиванні не виникає еліптичності. Єдине виключення – випадок повного внутрішнього відбивання, коли світло поширюється з більш оптично густого в менш оптично густе середовище під кутом, більшим за критичний. У цьому випадку виникає різниця фаз у ±π, що веде до перетворення лінійного поляризованого падаючого пучка в еліптично поляризований відбитий пучок. З формул Френеля знаходяться відповідні амплітудні коефіцієнти відбивання та заломлення:

.

На практиці визначаються не такі коефіцієнти відбивання, а відносні середні по періоду потоків відбитого та заломленого пучків до падаючого. Тобто вимірюються такі величини: ;…

Саме такі величини зображаються на графіку, який ілюструє кут Брюстера. Якщо показник заломлення середовищ збільшується, то початкова точка підіймається, а кут Брюстера зсувається вправо (в область більших значень).

Для часткових випадків розділення на p та s компоненти немає сенсу, тому записується лише один коефіцієнт відбивання і один коефіцієнт заломлення. При зручно від амплітудного представлення перейти до відносного показника заломлення: . У даному випадку знак «-» саме і означає стрибок фази на при відбиванні від оптично більш густого середовища.

Для заломлення . Тобто світло переходить в друге середовище без зміни фази. З цих виразів очевидно, що якщо два середовища дійсно прозорі, тобто немає поглинання, то ,як і повинно бути згідно закону збереження енергії. На практиці визначаються величини .

Наприклад, для скла n₂=1,52, для повітря n₁=1, звідси слідує .

Фазові співвідношення між p і s компонентами відбитої хвилі залежать від кута падіння, що також випливає з формул Френеля. При цьому виділяють випадки: кути падіння менші за кут Брюстера і кути падіння більші за кут Брюстера. При кутах, менших за кут Брюстера, p і s компоненти залишаються синфазними. При кутах, більших за кут Брюстера, співвідношення фаз ”стрибкоподібно” змінюються на . Саме цей випадок ілюструється першим рисунком даної теми. Припустимо, що падаючий пучок поляризований лінійно і містить як p, так і s компоненту. Тобто при відбиванні при будь-яких кутах еліптичність не виникає. Насправді в околі кута Брюстера виникає невелика еліптичність, яка не передбачається формулами Френеля. Це означає, що фаза змінюється від 0 до не стрибкоподібно, а плавно, хоча дуже швидко. Експеримент спостереження еліптичної поляризації в околі кута Брюстера. (рис)

Якби пучок був повністю поляризований лінійно, то його можна було б погасити з використанням лише лінійного аналізатора. У випадку еліптичної поляризації, що має місце в околі кута Брюстера, можна використати пару – аналізатор і платівку, яка компенсує різницю фаз до 0 або до π , тоді лінійно поляризований пучок може бути погашений при певному розташуванні аналізатора.

Пояснення відхилення від формул Френеля полягає в наступному: з фізичної точки зору властивості середовищ змінюються не стрибкоподібно на математичній границі розділу, а у деякому шарі скінченої товщини. Навіть якщо ширина такого шару мала у масштабі довжини хвилі світла, оптичні та фізичні характеристики такого шару відрізняються від характеристик всередині середовища. Показник заломлення при поверхневого шару може відрізнятись від показника заломлення основного шару аж до 15%. Оскільки такий шар дуже тонкий, він мало впливає на оптичні характеристики відбитого світла, тому відхилення від формул Френеля виявляються дійсно невеликими.