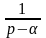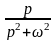- •1.Причины возникновения переходных процессов
- •Основные методы анализа переходных процессов в линейных цепях:
- •2. Законы коммутации
- •8.Алгоритм расчета переходных процессов классическим методом. Определение степени характеристического уравнении. Общая методика расчета переходных процессов классическим методом
- •9. Составление характеристического уравнения по выражению для входного сопротивления цепи.
- •10. Переходный процесс при подключении r-l цепи к источнику постоянной эдс
- •11. Переходный процесс при отключении катушки индуктивности с параллельным разрядным сопротивлением.
- •13. Включение r-l цепи на синусоидальное напряжение.
- •15. Переходный процесс при включении r-c цепи на постоянное напряжение.
- •16. Разрядка конденсатора.
- •Переходные процессы при подключении последовательной
- •19. Апериодический разряд конденсатора на цепь r-l
- •На рис. 5 представлены качественные кривые и , соответствующие колебательному переходному процессу при .
- •22. Включение r-l-c на постоянное напряжение
- •25. Понятие переходной проводимости и переходной функции.
- •Переходная функция по напряжению
- •26. Расчет переходных процессов с помощью интеграла Дюамеля
- •27. Применение интеграла Дюамеля при сложной форме напряжения
- •28. Закон Ома в операторной форме.
- •29. Первый закон Кирхгофа в опер форме
- •30. Второй закон Кирхгофа в опер форме
- •31. Последовательность расчета операторным методом
- •Последовательность расчета переходных процессов операторным методом
- •32. Теорема разложения. Формула разложения
- •33. Случаи уточнения формулы разложения
- •34. Расчет переходных процессов операторным методом при ненулевых начальных условиях.
- •35. Некорректные начальные условия. Первый и второй законы коммутации при некорректных начальных условиях.
- •36. Метод переменных состояний
- •37. Явный метод Эйлера при использовании метода переменных состояний
- •38. Метод Рунге-Кутта при использовании метода переменных состояний
- •39. Понятие о цепи с распределенными параметрами
- •40. Первичные параметры
- •41. Уравнение однородной длинной линии
- •42. Решение уравнений однородной длинной линии при установившимся синусоидальном режиме.
- •43. Вторичные параметры длинной линии
- •44. Основные характеристики бегущей волны. Графическое изображение прямой и обратной волны.
- •45. Уравнение однородной линии с гиперболическими функциями
- •47. Коэффициент отражения длинной линии
- •49, Линия включенная на согласованную нагрузку
- •50. Линия без искажения
- •51. Определение параметров длинной линии из опытов хх и кз
- •52. Линия без потерь. Уравнение линии без потерь.
- •53. Линия без потерь., согласованная с нагрузкой.
- •54. Линия без потерь, замкнутая на конце. Стоячие волны. Узлы и пучности.
- •55. Линия без потерь, разомкнутая на конце.
- •56. Линия без потерь нагруженная на реактивное сопротивление
- •57. Согласованная линия с нагрузкой. Короткозамкнутый шлейф. Четвертьволновый трансформатор.
- •58. Применение линии без потерь. Длинная линия как 4-х полюсник. Цепная схема.
- •Уравнения длинной линии как четырехполюсника
- •Уравнения переходных процессов в цепях с распределенными параметрами
- •60. Физический смысл решения уравнений переходных процессов в цепях . Энергия электрического и магнитного полей. Волна с прямоугольным фронтом.
- •61. Переходный процесс при включении на постоянное напряжение однородной линии.
- •62. Включение на постоянное напряжение линии нагруженной на активное сопротивление
- •63. Включение на постоянное напряжение разомкнутой на конце линии.
- •64. Включение на постоянное напряжение короткозамкнутой линии
- •73. Включение и отключение нагрузки в середине линии
- •Правило удвоения волны
- •74. Нелинейные элементы и их характеристики. Примеры практического применения нелинейных элементов
- •75. Управляемые нелинейные элементы. Статическое и дифференциальное сопротивление. Нелинейные электрические цепи постоянного тока
- •Параметры нелинейных резисторов
- •76. Графические методы расчета нелинейных электрических цепей. Последовательное и параллельное соединение элементов. Графические методы расчета
- •77. Расчет нелинейной цепи при смешанном соединении элементов графически Графические методы расчета
- •78. Расчет нелинейной цепи методом 2-х узлов.
- •79. Замена нелинейного сопротивления эквивалентным линейным сопротивлением и эдс
- •80. Расчет нелинейной цепи на основе теоремы об активном двухполюснике.
- •81. Понятие магнитной цепи. Основные величины для расчета магнитных цепей.
- •82. Индукционное и электродинамическое действия магнитного поля. Применение электромагнитных устройств.
- •83. Магнитомягкие и магнитотвердые материалы Магнитомягкие и магнитотвердые материалы
- •84. Первый и второй законы Кирхгофа для магнитных цепей Законы Кирхгофа и Ома для магнитных цепей
- •85. Понятие о магнитном сопротивлении и магнитной проводимости.
- •86. Вебер-Амперная характеристика. Аналогия электрических и магнитных цепей.
- •Вебер-Амперная характеритиска
- •87. Расчет магнитных цепей. Разветвленная цепь
- •2. “Обратная” задача для разветвленной магнитной цепи
- •88. Методы расчета магнитных цепей. Прямая и обратная задачи.
- •89. Магнитная цепь с постоянным магнитом. Особенности расчета.
- •90. Катушка с магнитопроводом на переменном токе как нелинейный индуктивный элемент. Метод эквивалентных синусоид.
- •91. Уравнение электрического состояния, векторная диаграмма и схема замещения катушки.
- •92. Последовательная и параллельная схемы замещения катушки.
- •93. Феррорезонанс при параллельном соединении катушки с ферромагнитным сердечником и конденсатора.
- •94. Феррорезонанс при параллельном соединении катушки и конденсатора.
- •95. Ферромагнитные стабилизаторы напряжения.
- •96. Катушка с ферромагнитным сердечником при одновременном намагничивании постоянным и переменным током.
- •97. Дроссель насыщения. Магнитный усилитель
- •98. Расчет переходного процесса в нелинейной цепи методом условной линеаризации
- •99. Расчет методом кусочно-линейной аппроксимации
- •100. Изображение процессов на фазовой плоскости.
28. Закон Ома в операторной форме.
Закон Ома в операторной форме
Пусть
имеем некоторую ветвь
![]() (см. рис. 1), выделенную из некоторой
(см. рис. 1), выделенную из некоторой

сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу, при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем случае ненулевые.
Для мгновенных значений переменных можно записать:
![]() .
.
Тогда на основании приведенных выше соотношений получим:
![]() .
.
Отсюда
 ,
(2)
,
(2)
где
 - операторное сопротивление рассматриваемого
участка цепи.
- операторное сопротивление рассматриваемого
участка цепи.
Следует
обратить внимание, что операторное
сопротивление
![]() соответствует комплексному сопротивлению
соответствует комплексному сопротивлению
![]() ветви в цепи синусоидального тока при
замене оператора р на
ветви в цепи синусоидального тока при
замене оператора р на
![]() .
.
Уравнение (2) есть математическая запись закона Ома для участка цепи с источником ЭДС в операторной форме. В соответствии с ним для ветви на рис. 1 можно нарисовать операторную схему замещения, представленную на рис. 2.

29. Первый закон Кирхгофа в опер форме
Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле,
равна нулю
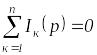 .
.
30. Второй закон Кирхгофа в опер форме
Второй закон Кирхгофа: алгебраическая сумма изображений ЭДС, действующих
в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура
![]() .
.
При записи уравнений по второму закону Кирхгофа следует помнить о необходимости учета ненулевых начальных условий (если они имеют место). С их учетом последнее соотношение может быть переписано в развернутом виде
![]() .
.
В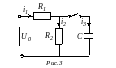 качестве примера запишем выражение для
изображений токов в цепи на рис. 3 для
двух случаев: 1 -
качестве примера запишем выражение для
изображений токов в цепи на рис. 3 для
двух случаев: 1 -
![]() ;
2 -
;
2 -
![]() .
.
В
первом случае в соответствии с законом
Ома
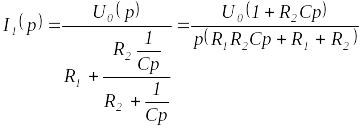 .
.
Тогда
![]()
и
![]() .
.
В о
втором случае, т.е. при
,
для цепи на рис. 3 следует составить
операторную схему замещения, которая
приведена на рис. 4. Изображения токов
в ней могут быть определены любым методом
расчета линейных цепей, например, методом
контурных токов:
о
втором случае, т.е. при
,
для цепи на рис. 3 следует составить
операторную схему замещения, которая
приведена на рис. 4. Изображения токов
в ней могут быть определены любым методом
расчета линейных цепей, например, методом
контурных токов:
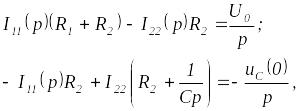
откуда
![]() ;
;
![]() и
и
![]() .
.
31. Последовательность расчета операторным методом
Сущность операторного
метода заключается в том, что функции
 вещественной переменной t,
которую называют оригиналом,
ставится в
соответствие функция
вещественной переменной t,
которую называют оригиналом,
ставится в
соответствие функция комплексной переменной
комплексной переменной
 ,
которую называют изображением.
В результате
этого производные и интегралы от
оригиналов заменяются алгебраическими
функциями от соответствующих изображений
(дифференцирование заменяется умножением
на оператор р,
а интегрирование – делением на него),
что в свою очередь определяет переход
от системы интегро-дифференциальных
уравнений к системе алгебраических
уравнений относительно изображений
искомых переменных. При решении этих
уравнений находятся изображения и далее
путем обратного перехода – оригиналы.
Важнейшим моментом при этом в практическом
плане является необходимость определения
только независимых начальных условий,
что существенно облегчает расчет
переходных процессов в цепях высокого
порядка по сравнению с классическим
методом.
,
которую называют изображением.
В результате
этого производные и интегралы от
оригиналов заменяются алгебраическими
функциями от соответствующих изображений
(дифференцирование заменяется умножением
на оператор р,
а интегрирование – делением на него),
что в свою очередь определяет переход
от системы интегро-дифференциальных
уравнений к системе алгебраических
уравнений относительно изображений
искомых переменных. При решении этих
уравнений находятся изображения и далее
путем обратного перехода – оригиналы.
Важнейшим моментом при этом в практическом
плане является необходимость определения
только независимых начальных условий,
что существенно облегчает расчет
переходных процессов в цепях высокого
порядка по сравнению с классическим
методом.
Изображение заданной функции определяется в соответствии с прямым преобразованием Лапласа:
 .
(1)
.
(1)
В сокращенной записи соответствие между изображением и оригиналом обозначается, как:
 или
или
 .
.
Следует отметить,
что если оригинал
увеличивается с ростом t,
то для сходимости интеграла (1) необходимо
более быстрое убывание модуля
 .
Функции, с которыми встречаются на
практике при расчете переходных
процессов, этому условию удовлетворяют.
.
Функции, с которыми встречаются на
практике при расчете переходных
процессов, этому условию удовлетворяют.
В качестве примера в табл. 1 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.
Таблица 1. Изображения типовых функций
Оригинал |
А |
|
|
|
|
|
Изображение |
|
|
|
|
|
|