
- •1.Причины возникновения переходных процессов
- •Основные методы анализа переходных процессов в линейных цепях:
- •2. Законы коммутации
- •8.Алгоритм расчета переходных процессов классическим методом. Определение степени характеристического уравнении. Общая методика расчета переходных процессов классическим методом
- •9. Составление характеристического уравнения по выражению для входного сопротивления цепи.
- •10. Переходный процесс при подключении r-l цепи к источнику постоянной эдс
- •11. Переходный процесс при отключении катушки индуктивности с параллельным разрядным сопротивлением.
- •13. Включение r-l цепи на синусоидальное напряжение.
- •15. Переходный процесс при включении r-c цепи на постоянное напряжение.
- •16. Разрядка конденсатора.
- •Переходные процессы при подключении последовательной
- •19. Апериодический разряд конденсатора на цепь r-l
- •На рис. 5 представлены качественные кривые и , соответствующие колебательному переходному процессу при .
- •22. Включение r-l-c на постоянное напряжение
- •25. Понятие переходной проводимости и переходной функции.
- •Переходная функция по напряжению
- •26. Расчет переходных процессов с помощью интеграла Дюамеля
- •27. Применение интеграла Дюамеля при сложной форме напряжения
- •28. Закон Ома в операторной форме.
- •29. Первый закон Кирхгофа в опер форме
- •30. Второй закон Кирхгофа в опер форме
- •31. Последовательность расчета операторным методом
- •Последовательность расчета переходных процессов операторным методом
- •32. Теорема разложения. Формула разложения
- •33. Случаи уточнения формулы разложения
- •34. Расчет переходных процессов операторным методом при ненулевых начальных условиях.
- •35. Некорректные начальные условия. Первый и второй законы коммутации при некорректных начальных условиях.
- •36. Метод переменных состояний
- •37. Явный метод Эйлера при использовании метода переменных состояний
- •38. Метод Рунге-Кутта при использовании метода переменных состояний
- •39. Понятие о цепи с распределенными параметрами
- •40. Первичные параметры
- •41. Уравнение однородной длинной линии
- •42. Решение уравнений однородной длинной линии при установившимся синусоидальном режиме.
- •43. Вторичные параметры длинной линии
- •44. Основные характеристики бегущей волны. Графическое изображение прямой и обратной волны.
- •45. Уравнение однородной линии с гиперболическими функциями
- •47. Коэффициент отражения длинной линии
- •49, Линия включенная на согласованную нагрузку
- •50. Линия без искажения
- •51. Определение параметров длинной линии из опытов хх и кз
- •52. Линия без потерь. Уравнение линии без потерь.
- •53. Линия без потерь., согласованная с нагрузкой.
- •54. Линия без потерь, замкнутая на конце. Стоячие волны. Узлы и пучности.
- •55. Линия без потерь, разомкнутая на конце.
- •56. Линия без потерь нагруженная на реактивное сопротивление
- •57. Согласованная линия с нагрузкой. Короткозамкнутый шлейф. Четвертьволновый трансформатор.
- •58. Применение линии без потерь. Длинная линия как 4-х полюсник. Цепная схема.
- •Уравнения длинной линии как четырехполюсника
- •Уравнения переходных процессов в цепях с распределенными параметрами
- •60. Физический смысл решения уравнений переходных процессов в цепях . Энергия электрического и магнитного полей. Волна с прямоугольным фронтом.
- •61. Переходный процесс при включении на постоянное напряжение однородной линии.
- •62. Включение на постоянное напряжение линии нагруженной на активное сопротивление
- •63. Включение на постоянное напряжение разомкнутой на конце линии.
- •64. Включение на постоянное напряжение короткозамкнутой линии
- •73. Включение и отключение нагрузки в середине линии
- •Правило удвоения волны
- •74. Нелинейные элементы и их характеристики. Примеры практического применения нелинейных элементов
- •75. Управляемые нелинейные элементы. Статическое и дифференциальное сопротивление. Нелинейные электрические цепи постоянного тока
- •Параметры нелинейных резисторов
- •76. Графические методы расчета нелинейных электрических цепей. Последовательное и параллельное соединение элементов. Графические методы расчета
- •77. Расчет нелинейной цепи при смешанном соединении элементов графически Графические методы расчета
- •78. Расчет нелинейной цепи методом 2-х узлов.
- •79. Замена нелинейного сопротивления эквивалентным линейным сопротивлением и эдс
- •80. Расчет нелинейной цепи на основе теоремы об активном двухполюснике.
- •81. Понятие магнитной цепи. Основные величины для расчета магнитных цепей.
- •82. Индукционное и электродинамическое действия магнитного поля. Применение электромагнитных устройств.
- •83. Магнитомягкие и магнитотвердые материалы Магнитомягкие и магнитотвердые материалы
- •84. Первый и второй законы Кирхгофа для магнитных цепей Законы Кирхгофа и Ома для магнитных цепей
- •85. Понятие о магнитном сопротивлении и магнитной проводимости.
- •86. Вебер-Амперная характеристика. Аналогия электрических и магнитных цепей.
- •Вебер-Амперная характеритиска
- •87. Расчет магнитных цепей. Разветвленная цепь
- •2. “Обратная” задача для разветвленной магнитной цепи
- •88. Методы расчета магнитных цепей. Прямая и обратная задачи.
- •89. Магнитная цепь с постоянным магнитом. Особенности расчета.
- •90. Катушка с магнитопроводом на переменном токе как нелинейный индуктивный элемент. Метод эквивалентных синусоид.
- •91. Уравнение электрического состояния, векторная диаграмма и схема замещения катушки.
- •92. Последовательная и параллельная схемы замещения катушки.
- •93. Феррорезонанс при параллельном соединении катушки с ферромагнитным сердечником и конденсатора.
- •94. Феррорезонанс при параллельном соединении катушки и конденсатора.
- •95. Ферромагнитные стабилизаторы напряжения.
- •96. Катушка с ферромагнитным сердечником при одновременном намагничивании постоянным и переменным током.
- •97. Дроссель насыщения. Магнитный усилитель
- •98. Расчет переходного процесса в нелинейной цепи методом условной линеаризации
- •99. Расчет методом кусочно-линейной аппроксимации
- •100. Изображение процессов на фазовой плоскости.
45. Уравнение однородной линии с гиперболическими функциями
 ,
,
47. Коэффициент отражения длинной линии

48. Входное сопротивление линии
Входным сопротивлением длинной линии (цепи с распределенными параметрами) называется такое сосредоточенное сопротивление, подключение которого вместо линии к зажимам источника не изменит режим работы последнего.
В
общем случае для линии с произвольной
нагрузкой
![]() для входного сопротивления можно
записать
для входного сопротивления можно
записать
![]() .
(1)
.
(1)
Полученное
выражение показывает, что входное
сопротивление является функцией
параметров линии
![]() и
и
![]() ,
ее длины
,
ее длины
![]() и нагрузки
.
При этом зависимость входного сопротивления
от длины линии, т.е. функция
и нагрузки
.
При этом зависимость входного сопротивления
от длины линии, т.е. функция
![]() ,
не является монотонной, а носит
колебательный характер, обусловленный
влиянием обратной (отраженной) волны.
С ростом длины линии как прямая, так
соответственно и отраженная волны
затухают все сильнее. В результате
влияние последней ослабевает и амплитуда
колебаний функции
уменьшается. При согласованной нагрузке,
т.е. при
,
не является монотонной, а носит
колебательный характер, обусловленный
влиянием обратной (отраженной) волны.
С ростом длины линии как прямая, так
соответственно и отраженная волны
затухают все сильнее. В результате
влияние последней ослабевает и амплитуда
колебаний функции
уменьшается. При согласованной нагрузке,
т.е. при
![]() ,
как было показано ранее, обратная волна
отсутствует, что полностью соответствует
выражению (1), которое при
трансформируется в соотношение
,
как было показано ранее, обратная волна
отсутствует, что полностью соответствует
выражению (1), которое при
трансформируется в соотношение
![]() .
.
Такой
же величиной определяется входное
сопротивление при
![]() .
.
При
некоторых значениях длины линии ее
входное сопротивление может оказаться
чисто активным. Длину линии, при которой
![]() вещественно, называют резонансной. Как
и в цепи с сосредоточенными параметрами,
резонанс наиболее ярко наблюдается при
отсутствии потерь. Для линии без потерь
на основании (1) можно записать
вещественно, называют резонансной. Как
и в цепи с сосредоточенными параметрами,
резонанс наиболее ярко наблюдается при
отсутствии потерь. Для линии без потерь
на основании (1) можно записать
![]() .
(2)
.
(2)
Из (2) для режимов холостого хода (ХХ) и короткого замыкания (КЗ), т.е. случаев, когда потребляемая нагрузкой активная мощность равна нулю, соответственно получаем:
![]() ;
(3)
;
(3)
![]() .
(4)
.
(4)
Исследование
характера изменения
![]() в зависимости от длины
линии на основании (3) показывает, что
при
в зависимости от длины
линии на основании (3) показывает, что
при
![]() по модулю изменяется в пределах
по модулю изменяется в пределах
![]() и имеет емкостный характер, а при
и имеет емкостный характер, а при
![]() - в пределах
- в пределах
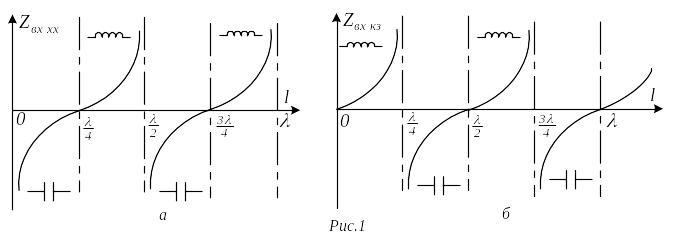
![]() и имеет индуктивный характер. Такое
чередование продолжается и далее через
отрезки длины линии, равные четверти
длины волны (см. рис. 1,а).
и имеет индуктивный характер. Такое
чередование продолжается и далее через
отрезки длины линии, равные четверти
длины волны (см. рис. 1,а).
В
соответствии с (4) аналогичный характер,
но со сдвигом на четверть волны, будет
иметь зависимость
![]() при КЗ (см. рис. 1,б).
при КЗ (см. рис. 1,б).
Точки,
где
![]() ,
соответствуют резонансу напряжений, а
точки, где
,
соответствуют резонансу напряжений, а
точки, где
![]() ,
- резонансу токов.
,
- резонансу токов.
Таким
образом, изменяя длину линии без потерь,
можно имитировать емкостное и индуктивное
сопротивления любой величины. Поскольку
длина волны
![]() есть функция частоты, то аналогичное
изменение
можно обеспечить не изменением длины
линии, а частоты генератора. При некоторых
частотах входное сопротивление цепи с
распределенными параметрами также
становится вещественным. Такие частоты
называются резонансными. Таким образом,
резонансными называются частоты, при
которых в линии укладывается целое
число четвертей волны.
есть функция частоты, то аналогичное
изменение
можно обеспечить не изменением длины
линии, а частоты генератора. При некоторых
частотах входное сопротивление цепи с
распределенными параметрами также
становится вещественным. Такие частоты
называются резонансными. Таким образом,
резонансными называются частоты, при
которых в линии укладывается целое
число четвертей волны.
