
- •1.Причины возникновения переходных процессов
- •Основные методы анализа переходных процессов в линейных цепях:
- •2. Законы коммутации
- •8.Алгоритм расчета переходных процессов классическим методом. Определение степени характеристического уравнении. Общая методика расчета переходных процессов классическим методом
- •9. Составление характеристического уравнения по выражению для входного сопротивления цепи.
- •10. Переходный процесс при подключении r-l цепи к источнику постоянной эдс
- •11. Переходный процесс при отключении катушки индуктивности с параллельным разрядным сопротивлением.
- •13. Включение r-l цепи на синусоидальное напряжение.
- •15. Переходный процесс при включении r-c цепи на постоянное напряжение.
- •16. Разрядка конденсатора.
- •Переходные процессы при подключении последовательной
- •19. Апериодический разряд конденсатора на цепь r-l
- •На рис. 5 представлены качественные кривые и , соответствующие колебательному переходному процессу при .
- •22. Включение r-l-c на постоянное напряжение
- •25. Понятие переходной проводимости и переходной функции.
- •Переходная функция по напряжению
- •26. Расчет переходных процессов с помощью интеграла Дюамеля
- •27. Применение интеграла Дюамеля при сложной форме напряжения
- •28. Закон Ома в операторной форме.
- •29. Первый закон Кирхгофа в опер форме
- •30. Второй закон Кирхгофа в опер форме
- •31. Последовательность расчета операторным методом
- •Последовательность расчета переходных процессов операторным методом
- •32. Теорема разложения. Формула разложения
- •33. Случаи уточнения формулы разложения
- •34. Расчет переходных процессов операторным методом при ненулевых начальных условиях.
- •35. Некорректные начальные условия. Первый и второй законы коммутации при некорректных начальных условиях.
- •36. Метод переменных состояний
- •37. Явный метод Эйлера при использовании метода переменных состояний
- •38. Метод Рунге-Кутта при использовании метода переменных состояний
- •39. Понятие о цепи с распределенными параметрами
- •40. Первичные параметры
- •41. Уравнение однородной длинной линии
- •42. Решение уравнений однородной длинной линии при установившимся синусоидальном режиме.
- •43. Вторичные параметры длинной линии
- •44. Основные характеристики бегущей волны. Графическое изображение прямой и обратной волны.
- •45. Уравнение однородной линии с гиперболическими функциями
- •47. Коэффициент отражения длинной линии
- •49, Линия включенная на согласованную нагрузку
- •50. Линия без искажения
- •51. Определение параметров длинной линии из опытов хх и кз
- •52. Линия без потерь. Уравнение линии без потерь.
- •53. Линия без потерь., согласованная с нагрузкой.
- •54. Линия без потерь, замкнутая на конце. Стоячие волны. Узлы и пучности.
- •55. Линия без потерь, разомкнутая на конце.
- •56. Линия без потерь нагруженная на реактивное сопротивление
- •57. Согласованная линия с нагрузкой. Короткозамкнутый шлейф. Четвертьволновый трансформатор.
- •58. Применение линии без потерь. Длинная линия как 4-х полюсник. Цепная схема.
- •Уравнения длинной линии как четырехполюсника
- •Уравнения переходных процессов в цепях с распределенными параметрами
- •60. Физический смысл решения уравнений переходных процессов в цепях . Энергия электрического и магнитного полей. Волна с прямоугольным фронтом.
- •61. Переходный процесс при включении на постоянное напряжение однородной линии.
- •62. Включение на постоянное напряжение линии нагруженной на активное сопротивление
- •63. Включение на постоянное напряжение разомкнутой на конце линии.
- •64. Включение на постоянное напряжение короткозамкнутой линии
- •73. Включение и отключение нагрузки в середине линии
- •Правило удвоения волны
- •74. Нелинейные элементы и их характеристики. Примеры практического применения нелинейных элементов
- •75. Управляемые нелинейные элементы. Статическое и дифференциальное сопротивление. Нелинейные электрические цепи постоянного тока
- •Параметры нелинейных резисторов
- •76. Графические методы расчета нелинейных электрических цепей. Последовательное и параллельное соединение элементов. Графические методы расчета
- •77. Расчет нелинейной цепи при смешанном соединении элементов графически Графические методы расчета
- •78. Расчет нелинейной цепи методом 2-х узлов.
- •79. Замена нелинейного сопротивления эквивалентным линейным сопротивлением и эдс
- •80. Расчет нелинейной цепи на основе теоремы об активном двухполюснике.
- •81. Понятие магнитной цепи. Основные величины для расчета магнитных цепей.
- •82. Индукционное и электродинамическое действия магнитного поля. Применение электромагнитных устройств.
- •83. Магнитомягкие и магнитотвердые материалы Магнитомягкие и магнитотвердые материалы
- •84. Первый и второй законы Кирхгофа для магнитных цепей Законы Кирхгофа и Ома для магнитных цепей
- •85. Понятие о магнитном сопротивлении и магнитной проводимости.
- •86. Вебер-Амперная характеристика. Аналогия электрических и магнитных цепей.
- •Вебер-Амперная характеритиска
- •87. Расчет магнитных цепей. Разветвленная цепь
- •2. “Обратная” задача для разветвленной магнитной цепи
- •88. Методы расчета магнитных цепей. Прямая и обратная задачи.
- •89. Магнитная цепь с постоянным магнитом. Особенности расчета.
- •90. Катушка с магнитопроводом на переменном токе как нелинейный индуктивный элемент. Метод эквивалентных синусоид.
- •91. Уравнение электрического состояния, векторная диаграмма и схема замещения катушки.
- •92. Последовательная и параллельная схемы замещения катушки.
- •93. Феррорезонанс при параллельном соединении катушки с ферромагнитным сердечником и конденсатора.
- •94. Феррорезонанс при параллельном соединении катушки и конденсатора.
- •95. Ферромагнитные стабилизаторы напряжения.
- •96. Катушка с ферромагнитным сердечником при одновременном намагничивании постоянным и переменным током.
- •97. Дроссель насыщения. Магнитный усилитель
- •98. Расчет переходного процесса в нелинейной цепи методом условной линеаризации
- •99. Расчет методом кусочно-линейной аппроксимации
- •100. Изображение процессов на фазовой плоскости.
40. Первичные параметры
Под первичными параметрами линии будем понимать сопротивление , индуктивность , проводимость и емкость , отнесенные к единице ее длины.
41. Уравнение однородной длинной линии
Для получения уравнений однородной линии разобьем ее на отдельные участки бесконечно малой длины со структурой, показанной на рис. 1.
П усть
напряжение и ток в начале такого
элементарного четырехполюсника равны
u и i, а в конце соответственно
и
.
усть
напряжение и ток в начале такого
элементарного четырехполюсника равны
u и i, а в конце соответственно
и
.
Разность напряжений в начале и конце участка определяется падением напряжения на резистивном и индуктивном элементах, а изменение тока на участке равно сумме токов утечки и смещения через проводимость и емкость. Таким образом, по законам Кирхгофа
или после сокращения на
; (1)
. (2)
Теорию цепей с распределенными параметрами в установившихся режимах будем рассматривать для случая синусоидального тока. Тогда полученные соотношения при можно распространить и на цепи постоянного тока, а воспользовавшись разложением в ряд Фурье – на линии периодического несинусоидального тока.
42. Решение уравнений однородной длинной линии при установившимся синусоидальном режиме.


43. Вторичные параметры длинной линии
Вводя комплексные
величины и заменяя
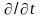 на
на
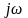 ,
на основании (1) и (2) получаем
,
на основании (1) и (2) получаем
 ;
(3)
;
(3)
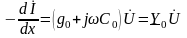 ,
(4)
,
(4)
где
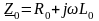 и
и
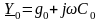 - соответственно комплексные сопротивление
и проводимость на единицу длины линии.
- соответственно комплексные сопротивление
и проводимость на единицу длины линии.
Продифференцировав
(3) по х
и подставив выражение
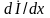 из (4), запишем
из (4), запишем
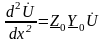 .
.
Характеристическое уравнение
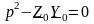 ,
,
откуда
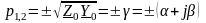 .
.
Таким образом,
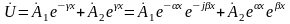 ,
(5)
,
(5)
где
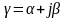 - постоянная распространения;
- постоянная распространения;
 - коэффициент затухания;
- коэффициент затухания;
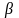 - коэффициент фазы.
- коэффициент фазы.
Для тока согласно уравнению (3) можно записать
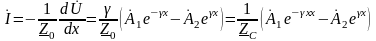 ,
(6)
,
(6)
где
 - волновое сопротивление.
- волновое сопротивление.
Волновое сопротивление
 и постоянную распространения
и постоянную распространения
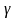 называют вторичными
параметрами линии,
которые характеризуют ее свойства как
устройства для передачи энергии или
информации.
называют вторичными
параметрами линии,
которые характеризуют ее свойства как
устройства для передачи энергии или
информации.
44. Основные характеристики бегущей волны. Графическое изображение прямой и обратной волны.
Определяя
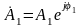 и
и
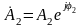 ,
на основании (5) запишем
,
на основании (5) запишем
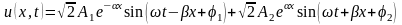 .
(7)
.
(7)
Аналогичное уравнение согласно (6) можно записать для тока.
Слагаемые в правой части соотношения (7) можно трактовать как бегущие волны: первая движется и затухает в направлении возрастания х, вторая – убывания. Действительно, в фиксированный момент времени каждое из слагаемых представляет собой затухающую (вследствие потерь энергии) гармоническую функцию координаты х, а в фиксированной точке – синусоидальную функцию времени.
В олну,
движущую от начала линии в сторону
возрастания х,
называют прямой,
а движущуюся
от конца линии в направлении убывания
х
– обратной.
олну,
движущую от начала линии в сторону
возрастания х,
называют прямой,
а движущуюся
от конца линии в направлении убывания
х
– обратной.
Характеризуется или коэффициентом бегучести волны (КБВ), или коэффициентом стоячести волны (KCB), или коэффициентом отражения Г, равным отношению амплитуд встречных волн
