7. Понятие функции

Функцией в математике называется отображение, которое однозначно отображает одни

значения на другие. Будем говорить, что функция f от аргумента X имеет значение y=f(x) .

У функции может быть произвольное количество аргументов, в том числе их может не быть совсем. Функция без аргументов имеет постоянное значение.

В общем случае функция может задавать отображение из нескольких множеств в множество значений.

Определение функции позволяет задать произвольное вычислимое отображение. Например, функцию, вычисляющую сумму квадратов, можно определить с помощью сложения и умножения:

аргументы: х,у

значение: х*х+у*у

Здесь X и у переменные, представляющие произвольные числа.

Вызов функции означает запуск, или применение определения функции к конкретным значениям аргументов. Например, применим функцию сумма квадратов к аргументам х=2 и у=3: сумма квадратов (2,3) -> 13

Для вызова функции, так и для записи выражений принята единообразная префиксная форма записи:

(+ X у), (- X у), (* X (+ у z)) и т.д.

В Лиспе объекты можно называть их естественными именами.

Лисп напоминает естественный язык и тем, что он обычно используется в диалоге и в режиме интерпретации.

Когда пользователь заканчивает ввод какого-либо вызова функции или другого выражения, то интерпретатор вычисляет и выдает значение этого выражения. Если мы хотим, например, вычислить выражение (+ 2 3), то введем его в машину и сразу получим результат:

Символ подчеркивания "_", показанный перед вводимым выражением, - это так называемое приглашение, при помощи которого интерпретатор дает знать, что он выполнил вычисление предыдущего выражения и ждет новое выражение.

Вычисляя значения выражения, интерпретатор Лиспа сначала пытается слева направо вычислить значения аргументов внешнего вызова. Если первый аргумент является константой или иным объектом, значение которого можно определить непосредственно, то вычисление аргументов вычисляемой функции можно продолжить. Если аргументом будет вложенный вызов функции или другая вычислимая форма, то перед ее вычислением определяются значения ее аргументов и т.д.

Наконец, опустившись на самый нижний уровень, можно начать в качестве значений аргументов предыдущего уровня подставлять значения, даваемые вложенными вычислениями. Последним возвращается значение всего выражения. Как и в математике, в Лиспе в первую очередь вычисляются выражения, заключенные в скобки:

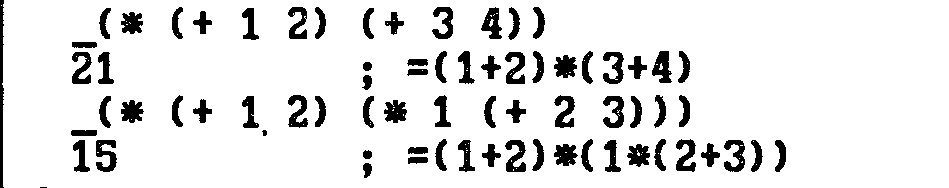
Выражения, которые интерпретатору не надо вычислять, нужно перед этим выражением поставить апостроф ‘ . В Лиспе начинающееся с апострофа выражение соответствует заключению в кавычки в обыкновенном тексте. Например:

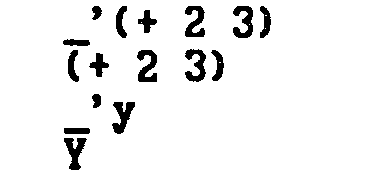
Апостроф перед выражением - это на самом деле сокращение лисповской формы QUOTE.

QUOTE можно рассматривать как специальную функцию с одним аргументом, которая ничего с ним не делает, даже не вычисляет его значение, а возвращает в качестве значения вызова сам этот аргумент.

Интерпретатор Лиспа, считывая начинающееся с апострофа выражение, автоматически преобразует его в соответствующий вызов функции QUOTE.

Перед числами и константами не надо ставить апостроф, так как интерпретатор считает, что они представляют самих себя.