25.Понятия. Числа. Символы. Списки. Строки. Последовательности. Массивы. Структуры.

Понятия

Типы данных - это подклассы используемых в языках программирования объектов данных. Простыми типами данных являются, например, целые и вещественные числа, строки, логические значения и т.д. Из них можно далее формировать составные типы.

Более точно под типом данных понимается множество значений, которые могут иметь одинаковые объекты или экземпляры данного типа. Необходимые объекты можно определить явно, перечислив их или их имена. Второй возможностью является определение объектов неявно в виде класса, описывая их структуру и свойства. В последнем случае обрабатываемые объекты создаются по мере необходимости.

В Лиспе используется как явный, так и неявный способы определения.

Под абстракцией данных понимают отделение свойств данных от самих объектов данных. Под абстрактным типом данных понимается тип данных, который определен через применимые к данному типу операции независимо от того, как представлены значения объектов данного типа.

Например, списки образуют абстрактный тип данных. Его объекты можно реализовать с помощью списочных ячеек и указателей или какой-нибудь другой структуры или типа данных. Базовые функции образуют множество операций (аксиомы типа). Их можно применять к спискам независимо от того, как последние реализованы на более низком уровне абстракции.

Для объектов, имеющих различные типы, нужны свои функции на базовом уровне. Кроме этого, для каждого типа нужен предикат, проверяющий принадлежность к этому типу. Например, (АТОМ x) проверяет, является ли X атомом. Наряду с предикатами, различающими типыв Коммон Лиспе используется и обобщенный предикат проверки типа:

(TYPEP объект тип)

Значением TYPEP будет истина, если объект является объектом данного типа:

Тип объекта можно определить и с помощью функции TYPE-OF, которая возвращает в качестве значения тип аргумента:

Наряду с множеством отдельных функций для преобразования одного типа в другой в Коммон Лиспе используется и обобщенная функция преобразования:

(COERCE объект тип)

Вызов COERCE преобразует объект, являющийся первым аргументом, к типу, задаваемому вторым аргументом. COERCE может также осуществлять преобразования между списками, строками и одномерными массивами, преобразовывать символы, состоящие из одного знака, строки и числа в соответствующие знаки и осуществлять преобразования между различными типами чисел.

Комплексные числа представляются в виде:

#C(x у)

где x - действительная, а у - мнимая компоненты числа. По префиксу #С можно отличить комплексное число от обычного двухэлементного списка. В качестве примера далее приведены изображения различных типов в Коммон Лиспе:

Числа

Наиболее общим числовым типом стандарта Коммон Лисп является NUMBER. Для него определены проверяющие знак и вид числа общеприменимые предикаты:

Вызов функции вычитания с одним аргументом возвращает число с измененным знаком, а функции ABS - абсолютную величину числа:

Для сравнения чисел используются следующие операции:

Операции сравнения допускают произвольное число аргументов (Об этом говорит ключевое слово &REST).

Арифметическими операциями являются:

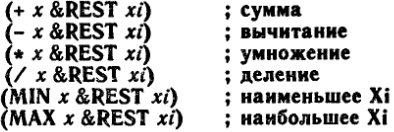
Удобной особенностью Коммон Лиспа являются обобщенные формы обновления INCF (increment function) и DECF (decrement function). Их можно выразить с помощью вызова SETF следующим образом:

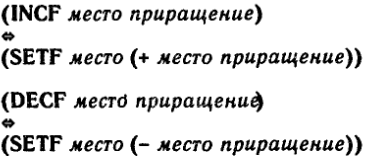
С их помощью можно увеличивать или уменьшать численные значения в ячейках памяти, например в переменных, элементах массива и т.д.

Формы обновления по своему эффекту и общности отличаются от вызовов 1+ и 1-, увеличивающих и уменьшающих значение:

В Коммон Лиспе имеется большой выбор определенных для всех чисел иррациональных и трансцендентных функций, таких как экспонента, логарифм и тригонометрические функции:

Аргументы следующих тригонометрических функций задаются в радианах и могут быть комплексными:

Число π является значением специальной переменной PI. Имеются гиперболические и обратные им функции:

Генератор случайных чисел (random number generator) Коммон Лиспа вызывается в форме:

Она генерирует строго меньшее, чем х неотрицательное случайное число (Точнее генерируемое случайное число принадлежит равномерному распределению, заданному на интервале [0,х)).

В стандарт Коммон Лиспа входят следующие типы чисел: рациональные числа (RATIONAL), числа с плавающей запятой (FLOAT) и комплексные числа (COMPLEX). Рациональные числа являются либо целыми числами (INTEGER), либо дробными числами (RATIO). Целые числа можно представлять с неограниченной точностью квадрат (BIGNUM) или довольствоваться целыми числами обыкновенного диапазона значений (FIXNUM), работа с которыми с вычислительной точки зрения более эффективна. Перед целым числом может стоять знак "+" или "-" и в его конце может быть десятичная точка.

Вот несколько функций и предикатов, определенных и используемых лишь для целых чисел:

Коммон Лисп содержит отсутствующую в традиционных языках программирования возможность использовать дробные числа без преобразования их в числа с плавающей запятой. Дробные числа изображаются знаком и двумя положительными числами, между которыми стоит дробная черта "/":

Если в результате вычислений получается сокращаемое число, то автоматически происходит сокращение числа до его канонической формы (canonical form).

Число с плавающей запятой состоит из знака (+ можно опустить), десятичного числа, записанного с использованием десятичной точки (мантисса) и отделенной знаком экспоненты экспоненциальной части, которая отображает порядок числа в терминах степени десяти:

Символы

С символом или с его именем могут быть связаны значение, определение функции и список свойств. Таким образом, символ является структурным объектом, состоящим из четырех компонент:

Кроме этого, с каждым символом связаны данные о том, какому пространству имен он принадлежит.

Для чтения и проверки значений различных системных свойств существуют свои предикаты и функции, приведенные в таблице.

Другими функциями, соответствующими системным свойствам символа, являются MACRO-FUNCTION, которая возвращает в качестве значения макроопределение, связанное с символом, и SPECIAL-FORM-P, с помощью которой можно проверить, есть ли у символа признак специальной формы. Предикат FBOUNDP возвращает значение Т, если с именем связано определение функции, специальная форма или макрос, иначе - значение NIL.

гй

С каждым символом связана строка, о которой говорят как о его внешнем представлении, или о печатном имени (print name, pname). Внешний облик символа хранится в виде строки, физически связанной с каждым символом. При выводе символа на дисплей J выводится его имя. Внешний облик списков определяется его атомами и разделяющими их пробелами (или

переводами строки) и ограничивающими скобками.

Имя символа при желании может содержать пробел, скобку или другой специальный символ, если воспользоваться знаком отмены - "обратной" косой чертой \ (backslash), который ставится перед специальным знаком. Другой способ включения в печатное имя атома ограничивающих или других специальных символов состоит в написании всего атома между вертикальными чертами | (bar). Это эквивалентно записи, в которой каждый знак атома специально выделен с помощью обратной косой черты:

Внешний вид (имя) символа можно изучить, превратив его в строку, например, функцией STRING, которая возвращает в качестве значения строку имени атома:

Имя можно разбить на знаки, составив из них список функцией COERCE:

Для создания символа можно использовать функцию INTERN, которая включает в систему (intern), вносит в список объектов и в пространство имен символ с именем, заданным строкой.

Символы можно создать и не включая их в систему. Для этого нужно использовать функцию

МАКЕ-SYMBOL:

Обычно в программировании на Лиспе используются лишь включенные в систему символы, чтобы применяемые в программе символьные имена имели одинаковый смысл. Если символы не включаются в систему, то с логически одинаковым именем из-за наличия физически различных символов могут быть связаны несколько различных значений, определений функции или других данных. Однако в некоторых случаях использование невключенных в систему символов может в некоторой мере сократить вычисления.

Для создания символов можно использовать и лисповский генератор символов (GENTEMP тело), который может порождать новые символы. Имя символа составляется из задаваемого в качестве необязательного аргумента начала и из порядкового номера порождаемого символа в качестве суффикса.

Списки

Точечная пара, или списочная ячейка, состоит из двух частей: полей CAR и CDR. Значением поля может быть произвольный лисповский объект (атом, знак, другой список, массив, структура и т.д.). Список можно определить через NIL и списочную пару следующим образом:

1) пустой список (), или NIL, является списком;

2) каждая точечная пара, поле CDR которой список, является списком.

Таким образом список - это связанная через поле CDR цепочка списочных ячеек, которая в поле CDR последней ячейки содержит NIL. Поля CAR этих ячеек представляют элементы списка.

Списки образуют в Коммон Лиспе тип LIST. Его подтипами являются зарезервированный для пустого списка NIL особый тип данных NULL и тип непустых списков CONS.

Набор действий со списками образует основной механизм представления данных в Лиспе, с помощью которого из объектов различных типов можно строить большие комплексы данных. Элементом списка так же, как и значением переменной, может быть произвольный лисповский объект. Используя списки, можно определять новые типы и структуры данных.

Ассоциативный список или просто а-список (a-list) - это структура данных, часто используемая в Лиспе и основанная на списках и точечных парах, для работы, с которой существуют готовые функции. Ассоциативный список состоит из точечных пар, поэтому его также называют списком пар:

Первый элемент пары (CAR) называют ключом (key) и второй (CDR) - связанными с ключом данными (datum). Обычно ключом является символ. Связанные с ним данные могут быть символами, списками или какими-нибудь другими лисповскими объектами. С помощью а-списка можно объединить разнотипные, поименованные ключами компоненты данных в единый комплекс данных.

С помощью встроенной функции PAIRLIS можно строить а-список из списка ключей и списка, сформированного из соответствующих им данных. Третьим аргументом является старый а-список, в начало которого добавляются новые пары:

(PAIRLIS ключи данные а-список)

Строки

Строка состоит из последовательности знаков (character). Знак также является типом данных. Его объекты в отличие от атомов, имя которых состоит из одного знака, изображаются в виде

#\x

В этой записи х является изображаемым данной записью знаком или словом в случае специального знака, обычно не имеющего печатного изображения.

Например:

Значением знака, как и у констант, является сам знак.

Является ли лисповский объект знаком, можно проверить предикатом (CHARACTERP х).

В строке знаки записываются в последовательности друг за другом, для ограничения которой с обеих сторон в качестве ограничителя используется знак ", например:

Если строку ввести в интерпретатор, то в качестве результата получим ту же строку. Строка не может представлять что-либо, кроме самой себя. Она является такой же константой, как числа и логические значения.

Функцией, проверяющей, имеет ли объект тип строки, является (STRINGP х), значением которой будет истина, если х - это строка.

В разных системах используются различные функции для преобразования атомов и списков в строки и наоборот. Преобразования в Коммон Лиспе можно осуществлять общей функцией COERCE или функцией STRING.

Произвольный элемент строки можно прочитать (т.е. сослаться на него с помощью индекса) функцией CHAR:

(CHAR строка n)

Последовательности

В Коммой Лиспе для упорядоченных множеств, или последовательностей, определен свой общий тип данных SEQUENCE. Его подтипами являются

- списки,

- векторы, или одномерные массивы.

Векторы наподобие списков содержат последовательность лисповских объектов, таких как атомы, числа, списки или другие векторы. Внешней формой представления векторов является

В отличие от списков векторы можно обрабатывать не только с помощью представленных здесь операций над последовательностями, но также и операциями над массивами, но не функциями, действующими над списками. К элементам вектора можно, например, эффективно обращаться напрямую, выбирать и присваивать им значения, задавая номер элемента.

Несмотря на представление, основанное на выделении кавычками, строки являются векторами, элементы которых - знаки. Исходя из этого, функции, предназначенные для работы с последовательностями, можно без оговорок применять и к строкам. То же самое относится и к действиям над массивами, которые применимым и к векторам.

Последовательность, таким образом, является довольно общим типом данных, содержащим в качестве подтипов основные типы данных Лиспа.

Последовательность можно создать с помощью функции MAKE-SEQUENCE:

У функции MAKE-SEQUENCE два обязательных и один необязательный ключевой параметр: INITIAL-ELEMENT. С его помощью при необходимости можно задать начальное значение для элементов создаваемой последовательности. Например:

На новый элемент можно сослаться вызовом:

(ELT последовательность n)

Для того чтобы изменить элемент, используется обобщенная функция присваивания SETF:

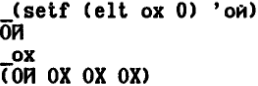
Функция ELT обобщает определенную для строк функцию CHAR и определенную для списков - NTH. Определенные для подтипов специальные функции эффективнее обобщенных форм.

Подпоследовательность последовательности можно построить вызовом:

Кроме этого, для последовательностей обобщены многие функции, упоминавшиеся в связи с работой над списками, это - LENGTH, REVERSE, REMOVE, DELETE, RPLACA, SOME и EVERY, которые можно применять и для векторов, и для строк:

Массивы

Массивы создаются формой:

Функция возвращает в качестве значения новый объект - массив, n1, n2, ..., nN - целые числа, их количество N отражает размерность (dimensionality) массива, а значения - размер (size) по каждой размерности. Необязательными аргументами (режимами) можно задать тип элементов массива, указать их начальные значения или придать самому массиву динамический размер. Общий размер массива в этом случае заранее знать и закреплять не обязательно.

Например: двумерный массив, представляющий точки дисплея с экраном 1024x1024, элементами которого являются числа с плавающей запятой одинарной точности и начальным значением 0.0, можно было бы создать следующим выражением:

Массивы подразделяются на универсальные массивы (general arrays), элементы которых могут содержать произвольный лисповский объект, и специализированные массивы (specialized arrays), про элементы которого известно, что они всегда одного типа (битовые, численные, строковые и т.п.).

Массив может иметь размерность 0, 1, 2, ... . 0-мерный массив состоит ровно из одного элемента. Одномерные массивы, или векторы (vectors), образуют важный специальный класс массивов. Для него кроме общих действий над массивами и последовательностями определены свои собственные действия.

Ссылка на элемент N-мерного массива осуществляется с помощью вызова:

nl, n2, ..., nN - координаты, или индексы (index), элемента, на который ссылаются. В качестве функции присваивания используется обобщенная функция присваивания SETF.

В следующем вызове строка трактуется как массив:

Кроме привычных массивов с численными индексами можно также работать с хэш-массивами (hash arrays).

Структуры

Для объединения основных типов данных (чисел, символов, строк, массивов) в комплексы, отображающие предметы, факты, ситуации предметной области, используется составной тип, который называется структурой, или записью (structure, record).

В структурах к одиночным данным и различным характеристикам можно обращаться по их логическим именам независимо от внутреннего строения структуры.

Программы имеют дело с суднами. Будем интересоваться следующими характеристиками судна: двумерные координаты (х,у) места его расположения, составляющие его скорости по каждой из координат и водоизмещение судна.

Отображающий класс судов универсальный (generic) тип структуры можно определить с помощью макроса DEFSTRUCT, формой которого (упрощенно) является

Например:

Символ СУДНО теперь определен как простой тип структуры, состоящий из компонент с именами X, Y, Х-СКОРОСТЬ, Y-CKOPOCTЬ и ТОННАЖ.

присваивания

DEFSTRUCT - это сложный макрос. Его вызов имеет много побочных эффектов, из которых наиболее существенным» являются: