23.Абстрактный подход в Лиспе.
Абстракция существенно основывалась на возможности представить отображения с помощью параметризированной лямбда-выражением общей формы. Лямбда-механизм можно с точки зрения такого абстрагирования данных назвать абстракцией отображения. Соответствующая техника применима и для определения функций более высокого порядка. Поскольку в них в качестве параметров и значений используются функции, то можно с помощью механизма параметризации абстрагировать сами функции, другими словами, способ вычислений. Параметризация может касаться первого элемента вызова функции, т.е. осуществляемых вычислений, а не только аргументов, как это происходит в абстракции отображения. Такая абстракция вычислений качественно отлична от связанной с данными абстракции отображений.
Далее для иллюстрации более абстрактных вычислений мы рассмотрим два способа действий:
1. Определение вычислений обычным образом в виде функционала, получающего функциональный аргумент.
2. Определение вычислений с помощью параметризованной функции с функциональным значением.
В обоих способах можно свободно применять различные виды рекурсии. Способы определения 1 и 2 можно между собой объединить, что приводит к использованию функционалов с функциональным значением.
Замещение функций одинакового вида функционалом является обобщением понятия подпрограммы. Если при использовании подпрограмм сходные элементы программы заменяются вызовом подпрограммы, то в случае функционального обобщения определения многих сходных подпрограмм заменяются функционалами
Абстракция построения представляет собой специальный образ действий, сокращающий длину записи. Хотя программа становится более короткой и формально более простой, ее понимание все же усложняется из-за высокого уровня абстракции.
Наряду с функционалами для абстрагирования вычислений также подходят функции с функциональным значением. С их помощью в зависимости от параметров можно строить лямбда-выражения, подбирать применяемые функции или создать замыкание, соответствующее данному вычислению. Например, следующая функция с функциональным значением КОМПОЗИЦИЯ возвращает в качестве значения замыкание, которое применяет обе функции, бывшие аргументами. КОМПОЗИЦИЯ является одновременно как функцией с функциональным значением, так и функционалом:
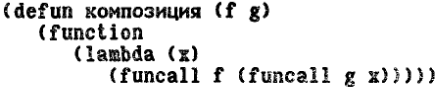
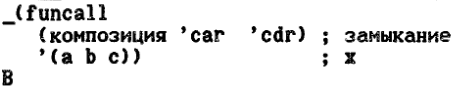
Действие функции КОМПОЗИЦИЯ основано на том, что возвращаемое ею замыкание в момент его применения "помнит" заданные в лямбда-выражении свободные переменные функции (здесь CAR и CDR). Функция КОМПОЗИЦИЯ является функциональной абстракцией, с помощью которой можно определить функцию, являющуюся композицией двух функций:
В этом случае композиция столь проста, что практической пользы от такого абстрагирования мало.
Функция с функциональным значением, предназначенная для абстрагирования повторяющихся вычислений, может, естественно, быть и рекурсивной.
Когда говорят о функциях более высокого порядка, рассматриваются автоаппликативные и авторепликативные функционалы как функции, которые получают или возвращают в качестве результата самих себя или точнее копии самих себя. В Лиспе их можно определить и использовать довольно просто.
Соответственно тому, как мы можем через функциональный аргумент определить авто-аппликативную рекурсивную функцию, мы можем определить и возвращающую себя рекурсивно функцию с функциональным значением.
Возьмем в качестве примера простейшую возможную функцию, которая возвращает себя в качестве результата. Это лямбда-выражение, примененное к такому же лямбда-выражению с формой QUOTE, т.е. это лямбда-вызов:
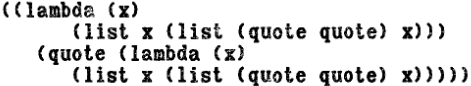
Форма является одновременно автоаппликативной. Она содержит изображение самой себя, но не целиком, поскольку такое изображение было бы бесконечно длинным. Изображение получается ограниченным благодаря механизму блокировки и лямбда-механизму, а также благодаря автоаппликации.
Автоаппликация как форма рекурсии с теоретической точки зрения очень интересна, но в практическом программировании, во всяком случае до настоящего времени, не находит особого применения. С нею связаны теоретические вопросы и проблемы, которые во многом еще не изучены.
Автофункции - это новый класс функций, которые отличаются от обыкновенных рекурсивных функций так же, как рекурсивные функции отличаются от не рекурсивных. Чтобы их можно было использовать в программировании столь же удобно, как и рекурсию, нужно использовать механизмы, которые при программировании учитывают инвариантные свойства вычислений таким же образом, как механизмы определения, вызова и вычисления функций учитывают рекурсию.