
- •1.Розв’язування показникових нерівностей.
- •§ 20. Розв'язування показникових рівнянь і нерівностей
- •2.Циліндр , його площа поверхні та об’єм.
- •Види циліндрів
- •Елементи циліндра
- •П лоща поверхні
- •Площа бічної поверхні
- •Площа загальна
- •3.Основні співвідношення між тригонометричними функціями одного і того ж аргументу.
- •§ 8. Співвідношення між тригонометричними функціями одного і того самого аргументу.
- •4.Піраміда , площа її поверхні та об’єм.
- •Формули
- •Властивості
- •5.Похідна , таблиця похідних.
- •6.Степені з раціональними показниками , їхні властивості.
- •8.Основні співвідношення між тригонометричними функціями одного аргументу.
- •§ 8. Співвідношення між тригонометричними функціями одного і того самого аргументу.
- •10.Призма , площа її поверхні та об’єм.
- •Площа поверхні
- •11.Елементарні перетворення графіків функцій.
- •12.Логарифмічна функція, її властивості та графік.
- •13.Розв’язування тригонометричних нерівностей. Розв’язування найпростіших тригонометричних нерівностей
- •14.Куля , площа поверхні та її об’єм.
- •15.Тригонометричні формули половинного аргументу (формули пониження степеня).
- •19.Квадратичні нерівності, їх розв’язання.
- •21.Показникова функція, її властивості та графік.
- •Властивості показникової функції.
- •22.Розв’язання лінійних нерівностей.
- •23.Найпростіші розв’язки тригонометричних рівнянь.
- •24.Розв’язування ірраціональних рівнянь.
- •25.Конус, його об’єм та площа поверхні.
- •Конус обертання
- •Площа поверхні конуса
- •Об'єм конуса
- •26.Тригонометричні функції подвійного кута.
- •27.Тригонометричні формули суми та різниці кутів.
- •28.Означення та властивості логарифмів.
- •29.Інтеграл, його властивості. Таблиця інтегралів.
- •30.Розв’язування логарифмічних нерівностей.
- •§ 23. Розв'язування логарифмічних рівнянь і нерівностей
25.Конус, його об’єм та площа поверхні.
Ко́нус — геометричне тіло, отримане шляхом об'єднання всіх променів, що виходять з однієї точки — вершини конуса, і таких що проходять через довільну плоску поверхню.
За ДСТУ: конус — узагальнений термін, під яким залежно від конкретних умов розуміють конічну поверхню, конічну деталь чи конічний елемент[1]
Іноді конусом називають частину такого тіла, отриману об'єднанням усіх відрізків, що з'єднують вершину і точки плоскої поверхні (яку в такому випадку називають основою конуса, а конус називають таким, що спирається на дану поверхню). Надалі буде розглядатися саме цей випадок, якщо не сказано про інше.
Відрізок, опущений перпендикулярно з вершини на площину основи (а також його довжина), називається висотою конуса. Якщо площа основи має скінченне значення, то об'єм конуса також має скінченне значення і дорівнює третині добутку висоти на площу основи. Таким чином всі конуси, що спираються на дану основу, і мають вершину в площині, паралельній цій основі, мають рівний об'єм, оскільки їх висоти рівні. Якщо основою конуса є многокутник, тоді конус стає пірамідою. Таким чином піраміди є підмножиною конусів.
Відрізок, що сполучає вершину конуса з точкою границі його основи називається твірною конуса. Множина всіх твірних конуса називається бічною поверхнею конуса.
Якщо основа конуса має центр симетрії (наприклад, є еліпсом) і ортогональна проекція вершини конуса на його основу збігається з цим центром, то конус називається прямим. При цьому пряма, що сполучає вершину конуса з центром його основи називається віссю конуса. Якщо ж ортогональна проекція вершини не збігається з центром основи, то такий конус називається косим.
Конус обертання
Якщо основою конуса є круг, то конус називають круговим. Прямий круговий конус (часто його називають просто конусом) можна отримати обертанням прямокутного трикутника навколо одного з катетів, який таким чином стане віссю конуса.
Перетин площини з прямим круговим конусом є одних з конічних перерізів (в невироджених випадках — еліпсом, параболою чи гіперболою, в залежності від розміщення січної площини).
Частина конуса, що лежить між основою і площиною, паралельною до основи і знаходиться між вершиною і основою, називається зрізаним конусом.
Конус, що спирається на еліпс, гіперболу чи параболу називається відповідно еліптичним, гіперболічним чи параболічним конусом (останні два мають нескінченний об'єм).
Площа поверхні конуса
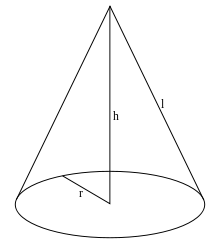

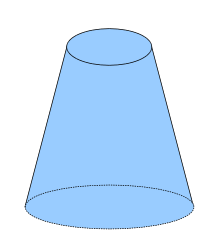 Прямий і похилий конуси
Прямий і похилий конуси
Прямий конус Зрізаний конус
Повна площа прямого кругового конуса
![]() ,
,
де r та l — радіус кола основи та довжина твірної бічної поверхні відповідно.
Площа бічної поверхні прямого кругового конуса
![]() ,
,
де r та l — радіус кола основи та довжина твірної бічної поверхні відповідно.
Об'єм конуса
У загальному випадку:
![]() ,
,
де S — площа основи, h — висота конуса.
Об'єм кругового конуса, відповідно:
![]() ,
,
26.Тригонометричні функції подвійного кута.
Формули подвійного аргументу
sin2α = 2sinα·cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
tg2α = 2tgα ⁄ (1-tg2α)
