23.Найпростіші розв’язки тригонометричних рівнянь.

24.Розв’язування ірраціональних рівнянь.

Ірраціональними називаються рівняння, у якиx змінна міститься під знаком кореня (радикала) або під знаком піднесення до дробового степеня.

В окремих випадках, не розв’язуючи дане ірраціональне рівняння, можна встановити, що воно не має коренів. Наприклад, рівняння не має коренів, бо арифметичний корінь не може бути від’ємним.

Рівняння не має розв’язків, бо обидва доданки є арифметичними коренями, а тому не можуть бути від’ємними. А сума двох невід’ємних чисел дорівнює нулю лише тоді, коли кожен доданок дорівнює нулю. Одночасно ж вирази і нулю дорівнювати не можуть.

Основними методами розв’язування ірраціональних рівнянь є метод піднесення обох частин рівняння до одного і того самого степеня та метод введення нових змінних.

При розв’язуванні ірраціональних рівнянь методом піднесення обох частин до парного степеня можуть з’явитися побічні корені. Це відбувається за рахунок того, що при піднесенні обох частин початкового рівняння до парного степеня дістаємо рівняння, що є результатом не тільки рівняння , але і рівняння , оскільки і , і . Так, наприклад, візьмемо рівняння . Піднісши обидві частини цього рівняння до квад-рата, дістанемо Коренями цього рівняння є числа Однак після перевірки переконуємось, що є коренем рівняння , а є побічним коренем.

Приступаючи до розв’язання ірраціонального рівняння, що містить парні степені радикалів, буває корисним знаходження області допустимих значень (ОДЗ), це, як правило, полегшує розв’язування рівняння. Якщо робити лише еквівалентні перетворення, то перевірку робити не потрібно.

Розглянемо рівняння виду . Очевидно, що ліва частина рівняння, яка містить радикал парного степеня, не може бути від’ємна, а отже невід’ємна і права частина даного рівняння. Враховуючи область допустимих значень, підкореневий вираз також не може бути від’ємним. Отже, рівняння виду рівносильне такій системі:

.

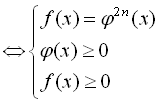Приклад 1. Розв’язати рівняння .

Розв’язання

Дане рівняння можна звести до вигляду , тобто

.

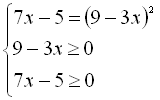
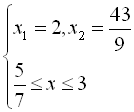З даної системи випливає, що лише є коренем початкового рівняння.

Відповідь: .

Розв’язання рівняння виду , де , здійснюється піднесенням обох частин рівняння до квадрату, «ізолюванням» радикала, який при цьому отримується, і повторним піднесенням обох частин рівняння до квадрата. В результаті таких перетворень рівняння даного виду зводиться до раціонального.

Приклад 2. Розв’язати рівняння .

Розв’язання

Область визначення даного рівняння визначається в результаті розв’-

язання системи нерівностей .

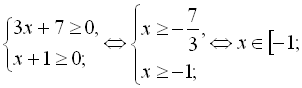
Перетворимо дане рівняння:

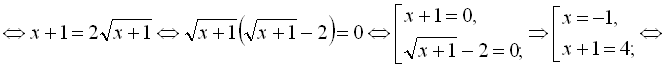
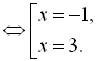
Обидва знайдені корені належать ОДЗ.

Відповідь: _.

Приклад 3. Розв’язати рівняння .

Розв’язання

Знайдемо для початку область допустимих значень: .

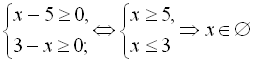Оскільки область допустимих значень виявилась пустою множиною, то і розв’язків дане рівняння не має.

Відповідь: .

Приклад 4. Розв’язати рівняння .

Розв’язання

Обидва підкореневі вирази є повними квадратами, тому

Тобто дане ірраціональне рівняння звелося до раціонального рівняння з двома модулями.

Приклад розв’язання рівняння такого типу наводився раніше.

Відповідь: .

Приклад 5. Розв’язати рівняння .

Розв’язання

Для розв’язання даного рівняння обираємо ІІІ систему:

.

Окремо розв’яжемо рівняння нашої системи. Методом підбору знаходимо цілий корінь даного рівняння. Для цього виписуємо дільники вільного члена: 1; 2; 3. При підборі знаходимо, що коренями є 2; 1; 3. Тоді

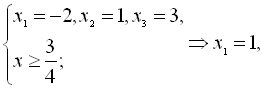
Відповідь:

Приклад 6. Розв’язати рівняння .

Розв’язання

Піднесемо обидві частини початкового рівняння до п’ятого степеня, дістанемо: , звідки .

Перевірка: Підставивши в початкове рівняння, дістанемо , тобто – правильна рівність є коренем.

Відповідь: .

Приклад 7. Розв’язати рівняння .

Розв’язання

ОДЗ початкового рівняння – всі дійсні числа. Піднесемо обидві частини рівняння до кубу:

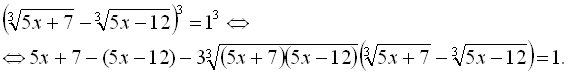
Замінимо різницю правою частиною первинного рівняння, тобто 1: .

Ізолюємо кубічний корінь, що залишився, і піднесемо обидві частини рівняння до кубу:

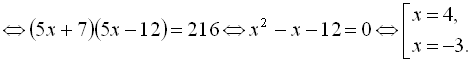
Виконавши перевірку, знайдемо, що множиною розв’язків даного рівняння є .

Відповідь: .

Приклад 9. Розв’язати рівняння .

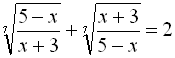Розв’язання

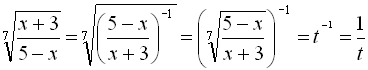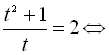
Зробимо заміну змінної, поклавши . Тоді . Звідси дістаємо Оскільки робилися лише еквівалентні перетворення, то початкове рівняння рівносильне такому: .

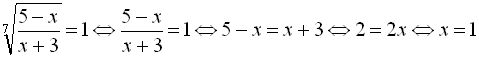При перевірці переконуємось, що – корінь вихідного рівняння.

Відповідь: .