
- •1.Розв’язування показникових нерівностей.
- •§ 20. Розв'язування показникових рівнянь і нерівностей
- •2.Циліндр , його площа поверхні та об’єм.
- •Види циліндрів
- •Елементи циліндра
- •П лоща поверхні
- •Площа бічної поверхні
- •Площа загальна
- •3.Основні співвідношення між тригонометричними функціями одного і того ж аргументу.
- •§ 8. Співвідношення між тригонометричними функціями одного і того самого аргументу.
- •4.Піраміда , площа її поверхні та об’єм.
- •Формули
- •Властивості
- •5.Похідна , таблиця похідних.
- •6.Степені з раціональними показниками , їхні властивості.
- •8.Основні співвідношення між тригонометричними функціями одного аргументу.
- •§ 8. Співвідношення між тригонометричними функціями одного і того самого аргументу.
- •10.Призма , площа її поверхні та об’єм.
- •Площа поверхні
- •11.Елементарні перетворення графіків функцій.
- •12.Логарифмічна функція, її властивості та графік.
- •13.Розв’язування тригонометричних нерівностей. Розв’язування найпростіших тригонометричних нерівностей
- •14.Куля , площа поверхні та її об’єм.
- •15.Тригонометричні формули половинного аргументу (формули пониження степеня).
- •19.Квадратичні нерівності, їх розв’язання.
- •21.Показникова функція, її властивості та графік.
- •Властивості показникової функції.
- •22.Розв’язання лінійних нерівностей.
- •23.Найпростіші розв’язки тригонометричних рівнянь.
- •24.Розв’язування ірраціональних рівнянь.
- •25.Конус, його об’єм та площа поверхні.
- •Конус обертання
- •Площа поверхні конуса
- •Об'єм конуса
- •26.Тригонометричні функції подвійного кута.
- •27.Тригонометричні формули суми та різниці кутів.
- •28.Означення та властивості логарифмів.
- •29.Інтеграл, його властивості. Таблиця інтегралів.
- •30.Розв’язування логарифмічних нерівностей.
- •§ 23. Розв'язування логарифмічних рівнянь і нерівностей
Властивості показникової функції.
Покажемо властивості показникової
функції
![]() у
вигляді таблиці для
0<а<1
і а>1.
у
вигляді таблиці для
0<а<1
і а>1.

0<а<1 |
|
Множина дійсних чисел |
Множина дійсних чисел |
Множина додатних чисел |
2. Область значень: Множина додатних чисел |
|
3. Функція зростає на всій області визначення |
|
4. Графік функції перетинає вісь Оу в точці (0;1). |
22.Розв’язання лінійних нерівностей.
Якщо число а менше або більше
від числа b, то записують відповідно
![]() або
або
![]() .
Наприклад,
.
Наприклад,
![]() ,
,
![]() .
Число а вважається більшим від b,
якщо різниця
.
Число а вважається більшим від b,
якщо різниця
![]() –
число додатне; число а менше від b,
якщо різниця
–
число від’ємне.
–
число додатне; число а менше від b,
якщо різниця
–
число від’ємне.
Нерівністю з однією змінною називається нерівність, що містить одну незалежну змінну. Розв’язком нерівності називається будь-яке значення змінної, при якому початкова нерівність зі змінною обертається у правильну числову нерівність. Розв’язати нерівність зі змінною – значить знайти всі її розв’язки або довести, що розв’язків немає. Дві нерівності називаються рівносильними (еквівалентними), якщо розв’язки цих нерівностей збігаються; зокрема, нерівності рівносильні, якщо вони не мають розв’язків.
Основні теореми про рівносильні нерівності.
1. Якщо з однієї частини нерівності перенести до іншої доданок із протилежним знаком, то дістанемо нерівність, рівносильну початковій.
2. Якщо до обох частин нерівності додати (або відняти) будь-яке число, то дістанемо нерівність, рівносильну початковій.
3. Якщо обидві частини нерівності помножити (поділити) на додатне число, то дістанемо нерівність, рівносильну початковій; якщо обидві частини нерівності помножити (поділити) на від’ємне число, то рівносильною початковій буде нерівність протилежного змісту.
Лінійною нерівністю з однією змінною
називається нерівність виду
![]() (або
(або
![]() )
або така, яка зводиться до неї.
)
або така, яка зводиться до неї.
Якщо
![]() ,
то нерівність
,
то нерівність
![]()
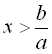
![]() (
(![]()
![]() ).
).
Якщо
![]() ,
то нерівність
,
то нерівність
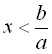 (
(![]()
![]() ).
).
Якщо
![]() ,
,
![]() ,
то нерівність набуває вигляду
,
то нерівність набуває вигляду
![]() і
вона правильна для будь-якого
(
).
і
вона правильна для будь-якого
(
).
Якщо
,
![]() ,
то нерівність розв’язків немає.
,
то нерівність розв’язків немає.
Приклад 1. Розв’язати нерівність
![]()
Розв’язання
Поділимо обидві частини нерівності на 4:
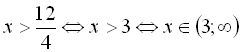 .
.
Приклад 2. Розв’язати нерівність
![]()
Розв’язання
![]()
Приклад 3. Розв’язати нерівність
![]()
Розв’язання
Перенесемо доданки зі змінними в одну
частину, а вільні члени – в іншу частину:
![]()
![]()
![]() .
.
Приклад 4. Розв’язати нерівність
![]() .
.
Розв’язання.
Розкриємо дужки:
![]() ,
,
зведемо подібні доданки:
![]()
![]()
![]() (6,6;
).
(6,6;
).
Система нерівностей
 справедлива
в тому і тільки в тому випадку, коли
обидві її нерівності справедливі.
Прикладом справедливої системи
нерівностей є система
справедлива
в тому і тільки в тому випадку, коли
обидві її нерівності справедливі.
Прикладом справедливої системи
нерівностей є система
 а
несправедливої – система
а
несправедливої – система
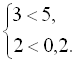 Аналогічний
зміст має і система нестрогих нерівностей
і система кількох (більше двох) нерівностей.
Аналогічний
зміст має і система нестрогих нерівностей
і система кількох (більше двох) нерівностей.
Подвійна нерівність
![]() справедлива
тоді і тільки тоді, коли справедлива
система нерівностей
справедлива
тоді і тільки тоді, коли справедлива
система нерівностей
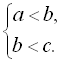
При розв’язуванні систем лінійних нерівностей, що складаються з двох нерівностей, можна зображати розв’язування за допомогою двох числових осей або за допомогою однієї осі, за допомогою дуг або без дуг, без допомоги штриховок або за допомогою штриховок, наносячи штриховки, які мають різний кут нахилу відносно числової прямої, знизу і згори або тільки згори (знизу).
Сукупність нерівностей
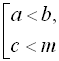 справедлива
в тому і тільки в тому випадку, коли
справедлива хоча б одна з її нерівностей.
Наприклад, сукупність нерівностей
справедлива
в тому і тільки в тому випадку, коли
справедлива хоча б одна з її нерівностей.
Наприклад, сукупність нерівностей
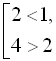 справедлива,
а сукупність нерівностей
справедлива,
а сукупність нерівностей
 –
несправедлива.
–
несправедлива.
Приклад 5. Розв’язати подвійну
нерівність:
![]()
Розв’язання
Дану подвійну нерівність можна записати у вигляді системи двох нерівностей:


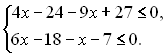
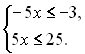
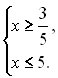

Розв’язування нерівностей можна
показати геометрично на числовій осі.
Так, якщо ми маємо строгу нерівність
![]() ,
то геометрично ця множина зображається
у вигляді тієї частини числової прямої,
яка лежить праворуч від точки з абсцисою
,
то геометрично ця множина зображається
у вигляді тієї частини числової прямої,
яка лежить праворуч від точки з абсцисою
![]() .
При цьому правіше точки
зазвичай
зображають у вигляді світлового кружечка
(говорять, що точку
«виколюють»).
.
При цьому правіше точки
зазвичай
зображають у вигляді світлового кружечка
(говорять, що точку
«виколюють»).

![]() (а;
).
(а;
).
![]() Якщо
маємо нестрогу нерівність
Якщо
маємо нестрогу нерівність
![]() ,
то на числовій осі наносять штриховку
ліворуч від точки
,
то на числовій осі наносять штриховку
ліворуч від точки
![]() ,
при цьому точку
звичайно
зафарбовують в чорний колір, тобто
зображають темною точкою.
,
при цьому точку
звичайно
зафарбовують в чорний колір, тобто
зображають темною точкою.

![]() .
.
На прикладі системи нерівностей покажемо чотири варіанти геометричної інтерпретації:
Приклад 6. Розв’язати систему
нерівностей і знайти всі її цілі розв’язки
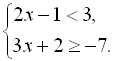
Розв’язання
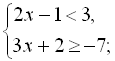

1-й варіант (з використанням двох числових осей):
2-й варіант (з використанням однієї числової осі і штриховок знизу і згори осі):

3-й варіант (з використанням однієї осі, дуг і штриховок).
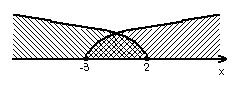
Шукана множина зображена подвійною штриховкою за допомогою накладання двох штриховок.
4-й варіант (з використанням однієї осі і дуг):

Штриховку наносимо лише там, де задані множини пересікаються.
Цілими розв’язками даної системи є значення – 3 ; – 2; – 1; 0; 1.
Відповідь:
![]()
![]() ;
– 3 ; – 2; – 1; 0; 1.
;
– 3 ; – 2; – 1; 0; 1.
