12.Логарифмічна функція, її властивості та графік.

Означення логарифмічної функції та її властивості (таблиця 1).

Функція виду у = , де > 0 і ≠ 1 називається логарифмічною. Вона є оберненою до показникової y = ( > 0 і ≠ 1).

13.Розв’язування тригонометричних нерівностей. Розв’язування найпростіших тригонометричних нерівностей

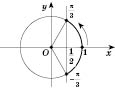Найзручнішим є спосіб розв’язування тригонометричних нерівностей за допомогою тригонометричного кола. Приклади 1) . Побудуємо одиничне коло (див. рисунок нижче). Проведемо пряму . Вона перетинає коло у двох точках. Одна з них відповідає куту або , друга — куту або . Ці дві точки розбивають коло на дві дуги. Точки однієї дуги мають абсцису, більшу за , другої дуги — меншу. Щоб описати всі точки потрібної дуги, «пройдемо» по ній у додатному напрямку, тобто проти годинникової стрілки. Ураховуючи періодичність функції , дістанемо відповідь: , n Є Z. 2) . Діючи аналогічно, отримаємо рисунок, на якому зображена пряма : 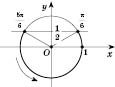Умову задачі задовольняють точки, що розташовані на колі нижче прямої . Але щоб записати проміжок, треба точку записати в другому вигляді. Для цього додамо до : . Ураховуючи період, дістанемо відповідь: при , n Є Z. 3) . Ураховуючи, що функція є зростаючою на кожному з проміжків виду , n Є Z, отримуємо , n Є Z. , , n Є Z. 

14.Куля , площа поверхні та її об’єм.

15.Тригонометричні формули половинного аргументу (формули пониження степеня).

Формули половинного аргументу

sin²(α⁄2) = (1-cosα) ⁄ 2

cos²(α⁄2) = (1+cosα) ⁄ 2

tg(α⁄2) = sinα ⁄ (1+cosα) = (1-cosα) ⁄ sinα, α≠π+2πk, kΖ

16.Визначений інтеграл. Формула Ньютона-Лейбніца.

17.Взаємне розташування прямих у просторі.

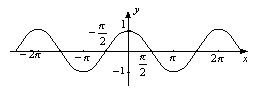
18. Функція y=cosx , її властивості та графік.

Властивості функції y=cosх: 1. Обл. визначення - проміжок (-∞;+∞). 2. Область значень – проміжок [-1;1]. 3. Функція парна, періодична з періодом Т=2П. 4. Функція зростає при -П+2Пn<х<2Пn, nє Z. 5. Функція спадає при 2Пn<х<П+2Пn, nє Z. 6. Функція має максимум у точках (2Пn;0), мінімум у точках (П+2Пn;0), nєZ.

19.Квадратичні нерівності, їх розв’язання.

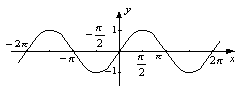
20. Функція y=sinx , її властивості та графік.

Тригонометрична функція задана формулою y=sinх Властивості функції y=sinх: 1. Область визначення - проміжок (-∞;+∞). 2. Область значень – проміжок [-1;1]. 3. Функція непарна, періодична з періодом Т=2П. 4. Функція зростає при -П/2+2Пn<х<П/2+2Пn, n є Z. 5. Функція спадає при П/2+2Пn<х<3П/2+2Пn, n є Z. 6. Функція має максимум у точках (П/2+2Пn;0), мінімум у точках (-П/2+2Пn;0), nє Z.

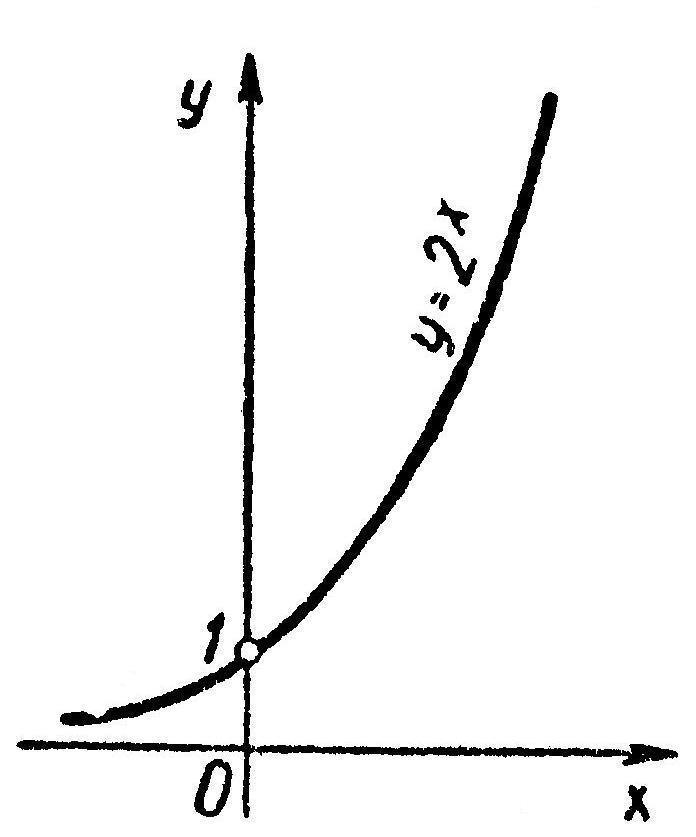
21.Показникова функція, її властивості та графік.

Означення. Функція виду де a не 0, а не 1, яка містить у показнику аргумент х, називається показниковою за основою а. Наведемо приклади показникових функцій: c

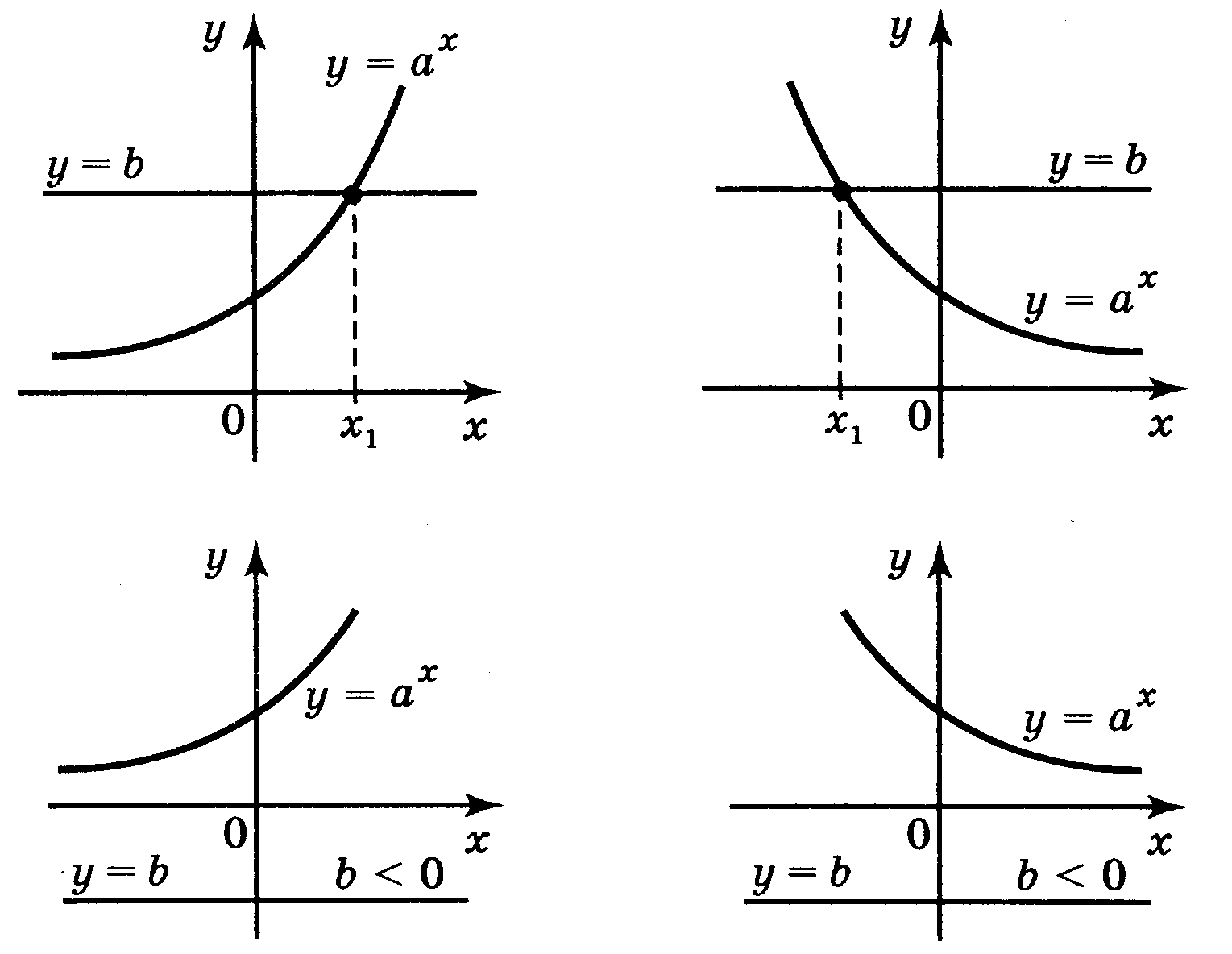
Головна особливість графіка цієї функції – її крутизна.

3. Побудова графіка показникової функції. Побудуємо графіки функцій для цього складемо таблицю:

Змінна х	-3	-2	-1	0	1	2	3
				1	2	4	8
	8	4	2	1

Побудуємо на координатній площині точки з таблиці і з’єднаємо їх плавною лінією.