10.Призма , площа її поверхні та об’єм.

Призмою називається многогранник, у якого дві грані — рівні n-кутники, розташовані в паралельних площинах, а решта n граней — паралелограми. Призма називається прямою, якщо її бічні ребра перпендикулярні до основи. Інші призми — похилі. Призма називається правильною, якщо вона пряма і її основи — правильні багатокутники. Висота призми — відстань між площинами її основ.

Об'єм

Об'єм призми дорівнює добутку площі основи на висоту. Таким чином об'єм дорівнює:

д е S — площа основи, h — висота. Об'єм правильної призми в основі якої є правильний n-кутник дорівнює:

Площа поверхні

Площа поверхні призми дорівнює , де S — площа основи, h — висота, P — периметр основи.

Площа поверхні правильної призми в основі якої є правильний n-кутник дорівнює:

11.Елементарні перетворення графіків функцій.

Загальний вид функції	Перетворення
y = f (x - a)	Паралельний перенос графіка вздовж осі абсцис на | A | одиниць вправо, якщо a> 0 ; вліво, якщо a <0 .
y = f (x) + a	Паралельний перенос графіка вздовж осі ординат на | A | одиниць вгору, якщо a> 0 , вниз, якщо a <0 .
y = f (- x)	Симетричне відображення графіка відносно осі ординат.
y = - f (x)	Симетричне відображення графіка відносно осі абсцис.
y = f (k x)	При k> 1 - Стиснення графіка до осі ординат в k разів, при 0 <k< i=""> <1 </k<> - Розтягнення графіка від осі ординат в 1 / k разів.
y = k f (x)	При k> 1 - Розтягнення графіка від осі абсцис в k разів, при 0 <k< i=""> <1 </k<> - Cжатіе графіка до осі абсцис в 1 / k разів.
y = | f (x) |	При - Графік залишається без змін, при f (x) <0 - Графік симетрично відображається щодо осі абсцис.
y = f (| x |)	При - Графік залишається без змін, при x <0 - Графік симетрично відображається щодо осі ординат.

Приклад 1.3. Побудувати графік функції .

Розв’язання

а) За вихідний беремо графік функції . Для зручності розглянемо побудову графіка тільки на одному періоді .

 

 

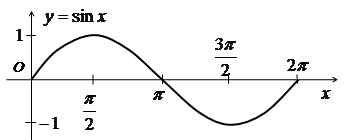
б) Оскільки , то стискаємо графік функції  в два рази вздовж осі Ox. Дістаємо графік функції .

 

 

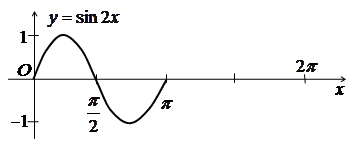
в) Розтягуємо графік функції  в три рази вздовж осі Oy, оскільки . Дістаємо графік функції .

 

 

г) Симетрично відобразивши останній графік відносно осі Ox, дістанемо графік функції .

 

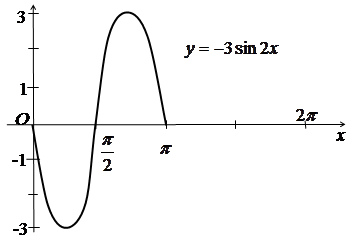
д) Отриманий графік паралельно переносимо на  вправо вздовж осі Ox, дістанемо графік функції  або .

 

 

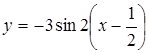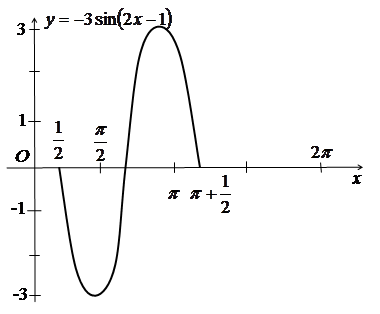
е) Нарешті, отриманий графік  паралельно перенесемо на дві одиниці вгору вздовж осі Oy, оскільки b=2>0. Дістанемо графік функції  (рис. 1.3).

Рис. 1.3

Приклад 1.4. Побудувати графік функції .

Розв’язання

Область існування функції: .

Поділивши чисельник на знаменник, дістанемо

 

, або .

 

 

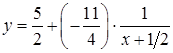Графік такої функції можна отримати з графіка функції  за допомогою таких перетворень:

а) паралельного перенесення графіка  вздовж осі абсцис на  одиниць вліво;

б) розтягування графіка а) вздовж осі ординат в  раз;

в) симетричного відображення графіка б) відносно осі абсцис;

в) паралельного перенесення вздовж осі ординат на  одиниць вгору.

Будуємо схематичний графік функції  (рис. 1.4).

 

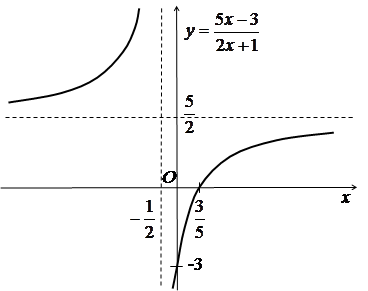
Рис. 1.4