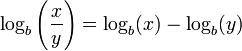27.Тригонометричні формули суми та різниці кутів.

Формули додавання

sin(α + β) = sinα·cosβ + cosα·sinβ

sin(α - β) = sinα·cosβ - cosα·sinβ

cos(α + β) = cosα·cosβ - sinα·sinβ

cos(α - β) = cosα·cosβ + sinα·sinβ

tg(α + β) = (tgα + tgβ) ⁄ (1 - tgα · tgβ)

tg(α - β) = (tgα - tgβ) ⁄ (1 + tgα · tgβ), α, β, α-β≠π⁄2+πk, kΖ

28.Означення та властивості логарифмів.

Логари́фм (від грец. λόγος — «слово», «відношення» і грец. ἀριθμός — «число») — математична операція обернена піднесенню до степеня.

Число називається логарифмом числа за основою якщо

Логарифми були введені Джоном Непером на початку 17 століття як засіб спрощення розрахунків. Вони швидко почали застосовуватися вченими та інженерами для пришвидшення виконання обчислень використовуючи логарифмічні лінійки і таблиць логарифмів. Наприклад, можна значно спростити обчислення добутку використовуючи важливу властивість: логарифм добутку є сумою логарифмів множників:

Сучасне означення логарифмів введено Леонардом Ейлером, який у 18 столітті пов'язав їх з показниковою функцією.

Позначення:

Існують особливі позначення для:

• натуральних логарифмів (логарифмів за основою e):

• десяткових логарифмів (логарифмів за основою 10):

• двійкових логарифмів (логарифмів за основою 2):

Логарифми були винайдені Джоном Непером на початку 17 століття як засіб для спрощення розрахунків і відтоді широко використовуються в науці, техніці. До винайдення комп'ютерів логарифмічна лінійка та таблиці логарифмів були повсякденним інструментом інженера.

	логарифм добутку двох чисел дорівнює сумі логарифмів цих чисел
	логарифм частки двох чисел дорівнює різниці логарифмів цих чисел
	логарифм степеня
	логарифм кореня

Графіки логарифмічної функції за основами (червоний), 10 (зелений) та 1,7 (фіолетовий). Графік асимптотично наближається до осі y.

Ці властивості зробили логарифм надзвичайно корисною функцією. Додавання та віднімання набагато простіші операції ніж множення та ділення, й, маючи таблицю логарифмів, можна сильно спростити складні обчислення.

Формула:

дозволяє переходити від одної основи до іншої.

Інші тотожності:

• 

• 

• 

• 

29.Інтеграл, його властивості. Таблиця інтегралів.

30.Розв’язування логарифмічних нерівностей.

§ 23. Розв'язування логарифмічних рівнянь і нерівностей

Логарифмічні рівняння. Приклади розв'язування логарифмічних рівнянь.

Логарифмічними називають рівняння, які містять невідому під знаком логарифма.

 

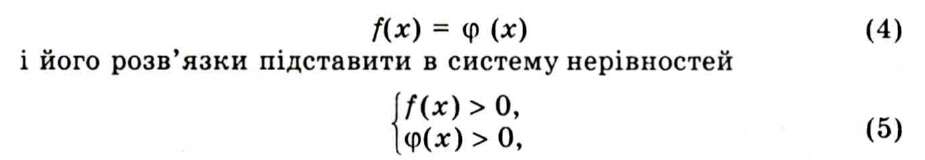
яка задає область визначення рівняння. Коренями рівняння (1) є тільки ті розв'язки рівняння (4), які задовольняють систему (5), тобто належать області визначення рівняння, заданого формулою (1).

Під час розв'язування логарифмічних рівнянь може відбутися розширення області визначення (з'являються сторонні корені) або її звуження (зникнуть корені). Тому треба обов'язково підставити корені рівняння (4) у систему (5).

Наприклад, рівняння lg х² = 2 має два корені, бо, за означенням логарифма, х² = 10², х² = 100, звідси x = 10; х₂ = -10. Якщо спочатку винести показник 2 за знак логарифма, то 2lg х = 2, lg х = 1, х = 10. Втрата другого розв'язку х = -10 сталася внаслідок звуження множини допустимих значень х після винесення показника за знак логарифма. Справді, в рівнянні lg х² = 2 корінь х може бути додатним і від'ємним числом, а в рівнянні 2 lg х = 2 — лише додатним.

Навпаки, якби заданим рівнянням було рівняння 2lg х = 2, а від нього ми перейшли б до рівняння lg х² = 2, а потім — до рівняння х² = 100, звідси x₁ = 10, х₂ = -10, то дістали б сторонній розв'язок (х₂ = -10) для даного рівняння.

Взагалі не існує якогось загального методу розв'язування логарифмічних рівнянь. Здебільшого воно зводиться до розв'язування алгебраїчних рівнянь і найпростіших логарифмічних рівнянь виду log_a х = Ь.

РОЗВ'ЯЗУВАННЯ ВПРАВ