1. Понятие метрики и метрического пространства, примеры.
Метрическое пространство — множество, в котором определено расстояние между любой парой элементов.
Метрика
(расстояние, функция расстояния) —
числовая функция
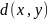(на множестве
,
точки
),
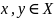которая удовлетворяет следующим
аксиомам (аксиомам расстояния):
1.
(аксиома тождества).
2.
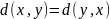(аксиома симметрии).
3.
(аксиома треугольника, неравенство
треугольника).
Метрическое
пространство — совокупность/пара
.
— некоторое множество (подлежащее
множество метрического пространства,
множество точек метрического
пространства).
— метрика; принимает
значения в множестве вещественных
чисел.
Обозначения.
Обычно расстояние
между точками
и
в метрическом пространстве
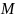обозначается
или
.
В метрической геометрии принято обозначение
или
,
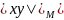если необходимо подчеркнуть, что речь
идет о
.
Реже употребляются обозначения
и
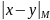.В классической геометрии приняты обозначения
или
(точки обычно обозначают заглавными
латинскими буквами).
Примеры:
Пространство изолированных точек. Для произвольного множествах X ф-ия расстояния:
,
если
.
во всех остальных случаях.
Дискретная метрика.Пространство действительных чисел. Метрика:
.
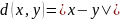Такое пространство называется
полным метрическим.Пространство векторов с вещественными координатами
.
Метрика:
.Пространство
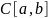непрерывных на отрезке
функций. Метрика:
.
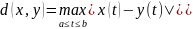Полное пространство — метрическое пространство, в котором каждая фундаментальная последовательность сходится (к элементу этого же пространства).
2. Сходящиеся и фундаментальные последовательности, открытые и замкнутые шары, полные метрические пространства.
Сходящаяся
последовательность (сходится к
)
— если
.
Т. е. если для всякого
найдется такое число
,
что для всех
имеет место
.
Фундаментальная
последовательность (сходящаяся
в себе последовательность, последовательность
Коши) — последовательность
точек метрического пространства такая,
что для любого заданного расстояния
существует элемент последовательности,
начиная с которого все элементы
последовательности находятся друг от
друга на расстоянии менее, чем заданное.
.
Открытый шар
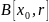в метрическом пространстве
— совокупность точек
,
удовлетворяющих условию
.
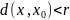Замкнутый шар
в метрическом пространстве
— совокупность точек
,
удовлетворяющих условию
.
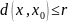— центр шара,
— радиус шара.
Пространство полное, если в метрическом пространстве каждая фундаментальная последовательность имеет предел.
3. Линейные нормированные пространства. Аксиомы нормы. Примеры определения норм в различных пространствах.
Множество становится пространством, когда в нем вводятся отношения (отношение порядка, расстояния).
Линейное пространство — частный случай метрического. В нем определены операции сложения и умножения на число.
Норма
вектора
— число, обозначаемое
и удовлетворяющее следующим
условиям — аксиомам нормы
(обобщающим свойства длины 3-мерного
в-ра):
1.
,
.
— нулевой вектор.
2.
,
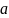— действительное число.
3.
— неравенство треугольника.
Линейное нормированное пространство — в котором задана норма.
Всякое нормированное — метрическое, не всякое линейное — нормированное.
Примеры определения норм в различных пространствах.
Норма в линейном пространстве — расстояние от 0 до элемента.
Евклидово пространство — конечномерное вещественное векторное пространство с введённым на нём скалярным произведением, порождающим норму:
Норма в евклидовом
пространстве:
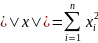— евклидова/сферическая норма
(простейший случай). Когда говорят о
евклидовой норме, не уточняя, обычно
имеют в виду сферическую.
Норма в линейном арифметическом пространстве : функция вида
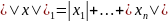— октаэдрическая
норма (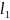
-норма).
Функция
,
заданная на векторах
в
— кубическая норма
(
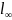-норма).
Единичная сфера
— множество векторов
нормированного пространства,
удовлетворяющих условию
(единичных векторов).
Зависит от линейного пространства и
однозначно определяет рассматриваемую
в нем форму.
На рис. 1 изображен вид единичной сферы для различных норм 2-мерного лин. пространства: сферической, октаэдрической, кубической.
На рис. 2 изображены единичные сферы указанных норм в 3-мерном лин. пространстве.
Вид единичной сферы для этих норм послужил источником для их названий.