15) Метод Лагранжа (метод вариации произвольных постоянных) — метод для получения общего решения неоднородного уравнения, зная общее решениеоднородного уравнения без нахождения частного решения.

Метод вариации произвольных постоянных для построения решения линейного неоднородного дифференциального уравнений

Метод состоит в замене произвольных постоянных   в общем решении

соответствующего однородного уравнения

на вспомогательные функции  , производные которых удовлетворяют линейной алгебраической системе

Определителем системы (1) служит вронскиан функций  , что обеспечивает её однозначную разрешимость относительно  .

Если   — первообразные для  , взятые при фиксированных значениях постоянных интегрирования, то функция

является решением исходного линейного неоднородного дифференциального уравнения. Интегрирование неоднородного уравнения при наличии общего решения соответствующего однородного уравнения сводится, таким образом, к квадратурам.

Метод вариации произвольных постоянных для построения решений системы линейных дифференциальных уравнений в векторной нормальной фор

состоит в построении частного решения (1) в виде

где   — базис решений соответствующего однородного уравнения, записанный в виде матрицы, а векторная функция  , заменившая вектор произвольных постоянных, определена соотношением  . Искомое частное решение (с нулевыми начальными значениями при   имеет вид

Для системы с постоянными коэффициентами последнее выражение упрощается:

Матрица   называется матрицей Коши оператора  .

16) Линейное дифференциальное уравнение с постоянными коэффициентами — обыкновенное дифференциальное уравнение вида: где

 — искомая функция,  — её  -тая производная,  — фиксированные числа,  — заданная функция (когда  , имеем линейное однородное уравнение, иначе — линейное неоднородное уравнение).Уравнение второго порядка[.Однородное уравнение второго порядка: интегрируется следующим образом:Пусть   — корни характеристического уравнения. ,являющегося квадратным уравнением.

Вид общего решения однородного уравнения зависит от значения дискриминанта  :

при   уравнение имеет два различных вещественных корня

Общее решение имеет вид:

при   — два совпадающих вещественных корня

Общее решение имеет вид:

при   существуют два комплексно сопряженных корня Общее решение имеет вид:

17) Метод неопределённых коэффициентов ― метод, используемый в математике для нахождения искомой функции в виде точной или приближённой линейной комбинации конечного или бесконечного набора базовых функций. Указанная линейная комбинация берётся с неизвестными коэффициентами, которые определяются тем или иным способом из условий рассматриРазложение дроби на простейшие[править]

Классическим примером применения метода неопределённых коэффициентов является разложение правильной рациональной дроби в комплексной или вещественнойобласти на элементарные дроби.

Пусть P и Q — многочлены с комплексными коэффициентами, причём степень многочлена P меньше степени многочлена Q. Будем полагать, что степень многочлена Q равна n, коэффициент при старшем члене многочлена Q равен 1, а  ,   ― различные корни многочлена Q с кратностями  , соответственно. Отсюда имеем

Функция P/Q представима, и притом единственным образом, в виде суммы элементарных дробей

где   ― неизвестные пока комплексные числа (их число равно n). Для их отыскания обе части равенства приводят к общему знаменателю. После его отбрасывания и приведения в правой части подобных членов получается равенство, которое сводится к системе линейных уравнений относительно  .Примечание. Нахождение коэффициентов упрощается, если Q имеет только некратные корни  ,  , т.е. все   и После умножения на z-z_k последнего равенства иподстановки z=z_k непосредственно получаем значение соответствующего коэффициента .Обращение ряда

Если функция f(x), не равная нулю при x=0 разложена в ряд Маклорена: то существует ряд Маклорена противоположной функции: Коэффициенты этого ряда можно найти, перемножив эти два равенства и применив метод неопределённых коэффициентов. Получится бесконечная треугольная система линейных уравнений, из которой последовательно найдутся искомые коэффициенты.Аналогичным, но более громоздким, образом можно найти коэффициенты ряда обратной функции: При этом используется соотношение g(f(x)=x, то есть весь ряд для f(x) подставляется вместо x в ряд для g(x).Сумма степеней[.В качестве частного примера можно привести задачу о нахождении формулы k-х степеней:  . Будем искать ответ в виде многочлена k=1-ой степени от n. Коэффициенты же этого многочлена найдём с помощью метода неопределённых коэффициентов.Пример. Ищем   в виде  .По определению  , а также p(1)=1. Подставляя многочлен в приведённой форме и приравнивая коэффициенты при одинаковых степенях, получаем систему для их определения:

откуда получаем ответ:  ваемой задачи. Обычно для них получается система алгебраических уравнений.

18) Определение 1.1 Если каждой совокупности значений "n" переменных из некоторого множества D этих совокупностей соответствует своё единственное значение переменной z, то говорят, что на множестве D задана функция "n" переменных.Множество D, указанное в определении 1.1, называется областью определяния илиобластью существования этой функции.Если рассматривается функция двух переменных, то совокупности чисел обозначаются, как правило, (x, y) и интерпретируются как точки координатной плоскости Oxy, а область определения функции z = f ( x, y ) двух переменных изобразится в виде некоторого множества точек на плоскости Oxy.Так, например, областью определения функции является множество точек плоскости Oxy, координаты которых удовлетворяют соотношению т. е. представляет собой круг радиуса r с центром в начале координат.Для функции областью определения служат точки, которые удовлетворяют условию т. е. внешние по отношению к заданному кругу.Часто функции двух переменных задаются в неявном виде, т. е. как уравнение связывающее три переменные величины. В этом случае каждую из величин x, y, z можно рассматривать как неявную функцию двух остальных.Геометрическим изображением (графиком) функции двух переменных z = f ( x, y )является множество точек P ( x, y, z) в трехмерном пространстве Oxyz, координаты которых удовлетворяют уравнению z = f ( x, y ).Графиком функции непрерывных аргументов, как правило, является некоторая поверхность в пространстве Oxyz, которая проектируется на координатную плоскость Oxy в область определения функции z= f ( x, y ).  Так, например, (рис. 1.1) графиком функции   является верхняя половина сферы, а графиком функции   - нижняя половина сферы. Графиком линейной функции z = ax + by + с является плоскость в пространстве Oxyz, а графиком функции z = сonst служит плоскость, параллельная координатной плоскости Oxyz.Заметим, что функцию трех и большего числа переменных изобразить наглядно в виде графика в трехмерном пространстве невозможно.В дальнейшем будем в основном ограничиваться рассмотрением функций двух или трех переменных, так как рассмотрение случая большего (но конечного) числа переменных производится аналогично

19)Производные высших порядков

Понятие производной произвольного порядка задаётся рекуррентно. Полагаем

Если функция f дифференцируема в x₀, то производная первого порядка определяется соотношением

Пусть теперь производная n-го порядка f⁽ⁿ⁾ определена в некоторой окрестности точки x₀ и дифференцируема. Тогда

Если функция u=f(x,y,z) имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от x,y,z  может иметь в некоторой точке   частные производные по той же или по любой другой переменной. Для исходной функции   эти производные будут частными производными второго порядка (или вторыми частными производными).

  или  

  или  

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,

Произво́дная(функции в точке)— основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

20) Полное приращение

Полное приращение, приращение, приобретаемое функцией нескольких переменных, когда все аргументы получают (вообще говоря, не нулевые) приращения Dx₁, Dx₂,..., Dx_n. При некоторых условиях (например, если все частные производные непрерывны) П. п. можно представить в виде суммы слагаемого, линейно зависящего от приращений аргументов и называемого полным дифференциалом, и слагаемого, бесконечно малого по сравнению с   

Дифференциа́л (от лат. differentia — разность, различие) — линейная часть приращения функции.

Обозначения

Обычно дифференциал функции f обозначается df. Некоторые авторы предпочитают обозначать df шрифтом прямого начертания, желая подчеркнуть, что дифференциал является оператором.

Дифференциал в точке   обозначается  , а иногда   или  , а также  , если значение   ясно из контекста.

Соответственно, значение дифференциала в точке   от f(x) может обозначаться как  ,  , а иногда   или  , а также  , если значение   ясно из контекста.

Использование знака дифференциала

• Знак дифференциала используется в выражении для интегр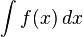ала  . При этом иногда (и не вполне корректно) дифференциал dx вводится как часть определения интеграла.

• Также знак дифференциала используется в обозначении Лейбница для производной 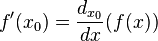 . Это обозначение мотивировано тем, что для дифференциалов функции f и тождественной функции x верно соотношение

Определения

Для функций

Дифференциал функции   в точке   может быть определён как линейная функция

где   обозначает производную f в точке  .

Таким образом   есть функция двух аргументов  .

Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функции   линейно зависящей от   и для которой верно следующее соотношение

Для отображений

Дифференциалом отображения   в точке   называют линейный оператор   такой, что выполняется условие

21) Дифференциал высшего порядка функции одной переменной

Для функции, зависящей от одной переменной z=f(x)  второй и третий дифференциалы выглядят так:

Отсюда можно вывести общий вид дифференциала n-го порядка от функции z=f(X) :

При вычислении дифференциалов высших порядков очень важно, что dx есть произвольное и не зависящее от x , которое при дифференцировании по x  следует рассматривать как постоянный множитель.

Дифференциал высшего порядка функции нескольких переменных

Если функция    имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так:  .

Символически общий вид дифференциала n-го порядка от функции   выглядит следующим образ где  , а    произвольные приращения независимых переменных  . Приращения    рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему. Сложность выражения дифференциалавозрастает с увеличением числа переменных.Неинвариантность дифференциалов высшего порядкаПри    ,  -й дифференциал не инвариантен (в отличие от инвариантности первого дифференциала), то есть выражение   зависит, вообще говоря, от того, рассматривается ли переменная x как независимая, либо как некоторая промежуточная функция другого переменного, например,  .Для доказательства неинвариантности дифференциалов высшего порядка достаточно привести пример. При n = 2 и    :если  x — независимая переменная, то   если     и   при этом,     и   С учётом зависимости  , уже второй дифференциал не обладает свойством инвариантности при замене переменной. Также не инвариантны дифференциалы порядков 3 и выше.