34.Правило Кирхгофа
Правила Кирхгофа (часто, в литературе, называются не совсем корректно Зако́ныКирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока.[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значение токов на всех ветвях цепи и все межузловые напряжения. Сформулированы Густавом Кирхгофом в 1845 году. Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами Природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (3-е уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
35.Закон Джоуля-Ленца
Закон Джо́уля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году ЭмилиемЛенцем[1].
В словесной формулировке звучит следующим образом[2]
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля
Математически может быть выражен в следующей форме:
где 
—
мощность выделения тепла в единице
объёма, 
—
плотность электрического
тока, 
— напряжённость
электрического поля, σ — проводимость среды.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке исопротивления участка
В математической форме этот закон имеет вид
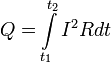
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 доt2. В случае постоянных силы тока и сопротивления:
36.Электрическая проводимость различных веществ
вещество |
См/м |
серебро |
62 500 000 |
медь |
58 100 000 |
золото |
45 500 000 |
алюминий |
37 000 000 |
магний |
22 700 000 |
иридий |
21 100 000 |
молибден |
18 500 000 |
вольфрам |
18 200 000 |
цинк |
16 900 000 |
никель |
11 500 000 |
железо чистое |
10 000 000 |
платина |
9 350 000 |
олово |
8 330 000 |
сталь литая |
7 690 000 |
свинец |
4 810 000 |
нейзильбер |
3 030 000 |
константан |
2 000 000 |
манганин |
2 330 000 |
ртуть |
1 040 000 |
нихром |
893 000 |
графит |
125 000 |
вода морская |
3 |
земля влажная |
10−2 |
вода дистилл. |
10−4 |
мрамор |
10−8 |
стекло |
10−11 |
фарфор |
10−14 |
кварцевое стекло |
10−16 |
янтарь |
10−18 |