10. Энергия гармонического осциллятора.

Гармоническим осциллятором называется система, совершающая колебания, описыва­емые уравнением вида

Во время колебательных процессов происходит периодическое превращение потенциальной энергии системы в кинетическую. Например, отклонив математический маятник в сторону и, следовательно, подняв его на высоту h, ему сообщают потенциальную энергию  . Она полностью переходит в кинетическую энергию движения  , когда груз проходит положение равновесия и скорость его максимальна. При колебаниях пружинного маятника кинетическая энергия движения груза переходит в потенциальную энергию деформированной системы. Величина полной энергии колеблющейся системы в любой момент времени равна сумме ее кинетической и потенциальной энергии:

или

(7.2)

Поскольку скорость – это первая производная от координаты по времени, то

.

Учитывая, что   и подставив выражения для x и V, получим:

.

То есть полная энергия системы, совершающей колебания, пропорциональна ее массе, квадрату амплитуды и квадрату собственной частоты. Так как силы, действующие на колеблющуюся частицу, являются консервативными, то ее механическая энергия остается постоянной. В процессе же колебаний происходит превращение кинетической энергии в потенциальную и обратно.

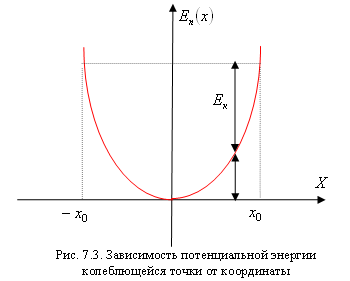
На рис. 7.3 приведен график зависимости потенциальной энергии от координаты частицы. С ростом x уменьшается кинетическая энергия и увеличивается потенциальная. Максимального значение потенциальная энергия достигает в поворотных точках  , при этом кинетическая энергия равна нулю. Среднее за период значение кинетической энергии равно среднему за период значению потенциальной энергии.

11. Сложение колебания одинакового направления. Биения.

Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты. Смещение х колеблющегося тела будет суммой смещений х1 и х2 которые запишутся следующим образом:

х1 = а1 cos (оt + 1), (27.12) 

х2 = а2 cos (оt + 2).

 Вспомним описание гармонических колебаний в виде векторной диаграмм (рис.27.7) и представим оба колебания с п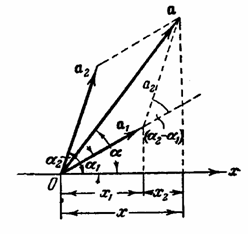 омощью векторов a1 и а2 (рис. 27.8). Построим по правилам сложения векторов результирующий вектор а. Легко видеть, что проекция этого вектора на ось х равна сумме проекций слагаемых векторов:

х = х1 + х2.

Рис.27.7. Рис.27.8.

Следовательно, вектор а представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью о, как и векторы a1 и а2, так что результирующее движение будет гармоническим колебанием с частотой о, амплитудой а и начальной фазой . Из построения (и из теоремы косинусов) следует, что  (27.13)  (27.13)

.

Проанализируем выражение (27.12) для амплитуды. Если разность фаз обоих колебаний (2 - 1) равна нулю, амплитуда результирующего колебания равна сумме а1 и a2. Если разность фаз (2 - 1) равна + или -, т. е. оба колебания находятся в противофазе, то амплитуда результирующего колебания равна а1 – а2.

Если частоты колебаний х1 и х2 неодинаковы, векторы a1 и а2 будут вращаться с различной скоростью. В этом случае результирующий вектор а пульсирует по величине и вращается с непостоянной скоростью. Следовательно, результирующим движением будет в этом случае не гармоническое колебание, а некоторый сложный колебательный процесс.

Биения.

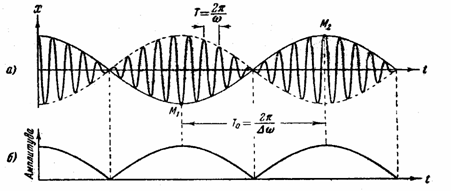
Особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. Как мы сейчас покажем, результирующее движение при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такое колебание называется биениями.

Обозначим частоту одного из колебаний , частоту второго колебания через  + . По условию <<. Амплитуды обоих колебаний будем полагать одинаковыми и равными а. Поскольку частоты колебаний несколько отличны, всегда можно выбрать начало отсчета времени так, чтобы начальные фазы обоих колебаний были равны нулю. Практически это означает, что мы должны дождаться, пока смещения в обоих колебаниях достигнут одновременно наибольшего положительного значения, и в этот момент «запустить секундомер». Тогда уравнения обоих колебаний будут иметь следующий вид:

x1 = a cos t, 

x2 = a cos ( +)t.

Складывая эти два выражения и применяя тригонометрическую формулу для суммы косинусов  , получаем:

x = x1 + x2 =  (27.15)

(во втором множителе пренебрегаем членом /2 по сравнению с ).

Рис.27.9. Формирование биений.

График функции (27.15) изображен на рис. 27.9, а.

График построен для  .

Заключенный в скобки множитель в формуле (27.15) изменяется гораздо медленнее, чем второй множитель. Ввиду условия << за то время, за которое множитель cos t совершает несколько полных колебаний, множитель, стоящий в скобках, почти не изменится. Это дает нам основание рассматривать колебание (27.15) как гармоническое колебание частоты , амплитуда которого изменяется по некоторому периодическому закону. Выражением этого закона не может быть множитель, стоящий в скобках, так как он изменяется в пределах от -2а до +2а, в то время как амплитуда по определению - положительная величина. График амплитуды показан на рис.27.9,б. Аналитическое выражение амплитуды, очевидно, имеет вид:

амплитуда =  . (27.16)

Параметрические системы описываются линейными дифференциальными уравнениями с переменными коэффициентами, т.е. коэффициентами, зависящими от аргумента (времени). Нелинейные системы описываются нелинейными дифференциальными уравнениями, т.е. уравнениями с коэффициентами, зависящими от функции (тока, напряжения). Для нелинейных систем принцип суперпозиции не выполняется. В параметрических и нелинейных системах происходит деформация спектра входного сигнала. Кроме такой классификации колебательные системы можно разделить на дискретные (с сосредоточенными параметрами) и сплошные (с распределенными параметрами).