40.Частные случаи приведения пространственной системы сил к простейшим системам.

№	Значения главного вектора и главного момента	Результат приведения
1		Система сил приводится к паре сил, момент которой равен главному моменту   (главный момент системы сил не зависит от выбора центра приведения О).
2		Система сил приводится к равнодействующей, равной  , проходящей через центр О.
3		Система сил приводится к равнодействующей  , равной главному вектору   и параллельной ему и отстоит от него на расстоянии  . Положение линии действия равнодействующей должно быть таким, чтобы направление ее момента относительно центра приведения О совпадало с направлением   относительно центра О.
4	, причем векторы   и   не перпендикулярны	Система сил приводится к динаме (силовому винту) – совокупности силы   и  пары сил, лежащей в плоскости, перпендикулярной к этой силе.
5		Система сил, приложенных к твердому телу, является уравновешивающейся.

41.Частные случаи равновесия твердого тела.Равновесие твердого тела с двумя неподвижными точками

Теорема. Три силы уравновешивают твёрдое тело только в том случае, когда все они лежат в одной плоскости.

 Доказательство.

Выберем за точку приведения точку на линии действия третьей силы. Тогда   (рис.22)

 

Рис.22.

 

То есть плоскости  S1 и  S2 совпадают, причём для любой точки на оси силы   , ч.т.д. (Проще:    в плоскости    только там же для уравновешивания).

Условия равновесия твёрдого тела с одной неподвижной точкой.

Центр приведения – закреплённая точка (рис.23):

 

Рис.23.

        Моменты (условия равновесия):

 

Для определения реакций => результирующая:

   ;     ;       .

Условия равновесия твёрдого тела, способного вращаться вокруг неподвижной оси.

 

Рис.24.

Закреплены две точки О и О1. Центр приведения: точка О (рис.24).

 ; Rx, Ry, Rz в точке О; R`x, R`y, R`z в точке О1; ОО1 = h.

Уравнения равновесия:

 Положение тела в пространстве определяется одним параметром, например, углом поворота  , который определяется из последнего уравнения:   . Остальные 5-ть уравнений => нахождение 6-ти проекций реакций связи => задача статически неопределимая. Требуются дополнительные условия деформирования (в сопротивлении материалов).

 Условия равновесия твёрдого тела, способного перемещаться параллельно неподвижной плоскости (рис.25).

 

Рис.25.

 Уравнения равновесия:

 где  ,  ,  – проекции активных сил, приложенных в точках ( ,  ,  ).

Два первых и последнее уравнения – необходимые условия равновесия. Три остальных => реакции, то есть только для закрепления в трёх точках. Иначе => статически неопределимая задача.

 Случай опоры на три точки.

Для определения реакций имеем:

   ,

где   ,

        .

Решение имеется только при условии:

   ,

то есть три точки опоры не лежат на одной прямой. Иначе, статическая неопределимость.

41. Для равновесия плоской системы сил, приложенной к твердому телу, н необходимо и достаточно, чтобы главный вектор и главный момент системы р равнялись нулю:

, .

Относительно неподвижной оси:

, ,

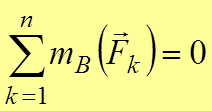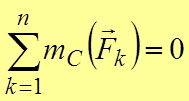
42. Силу, приложенную к твердому телу можно переносить параллельно ей самой в любую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда переносится сила.

Пусть на твердое тело в точке А действует сила  . (рис. 28 ).

Ее действие не изменится если в любой точке тела В, приложить две уравновешенные силы  .

Полученная система трех сил и представляет собой силу   равную  , но приложенную в точке В, и пару   с моментом

что и требовалось доказать.

На рисунке 28, б можно видеть, что мы перенесли силу   из точки А в точку В и стрелкой указали, что добавили момент m согласно формуле (4.1.1).

43. Центр параллельных сил – точка, через которую проходит линия действия равнодействующей системы параллельных сил F_k при любом повороте всех этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол. Координаты центра параллельных сил определяются формулами: Условия равновесия произвольной пространственной системы силПроизвольной пространственной системой сил называется система сил, линии действия которых не лежат в одной плоскости.

Согласно основной теореме статики (теореме Пуансо) любую произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы (главного вектора системы) и пары сил (главного момента системы сил).

Отсюда вытекает условие равновесия произвольной пространственной системы сил.

В геометрической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю R = 0,  M_o = 0.

В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси и суммы моментов всех сил относительно этих осей были равны нулю ΣF_kx = 0,    ΣF_ky = 0,    ΣF_kz = 0, M_x(F_k) = 0,     M_y(F_k) = 0,    M_z(F_k) = 0.

Условия равновесия могут быть использованы для решения задач на равновесие при определении неизвестных величин (реакций связей). 

Чтобы задача была статически определимой, число неизвестных должно быть не более шести.

В частности, для системы параллельных сил условиями равновесия являются следующие равенства

 ΣF_kx = 0,    M_x(F_k) = 0,    M_y(F_k) = 0.