Початкові фази першого і другого коливань відповідно дорівнюють

Проведемо обчислення:

с^-1,

Зобразимо вектори і . Для цього відкладемо відрізки довжиною = 3 см і = 2 см під кутами = 30⁰ і = 60⁰ до осі Ох. Результуюче коливання відбуватиметься з тією ж частотою і амплітудою А, що дорівнює геометричній сумі амплітуд і : . Згідно з теоремою косинусів

Початкову фазу результуючого коливання можна також визначити безпосередньо з векторної діаграми (рис.49):

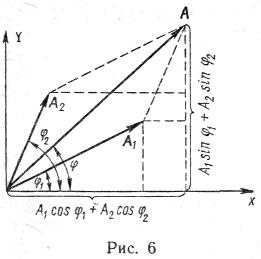
Рисунок 49 – Додавання коливань, що відбуваються у одному напрямку

(60)

Проведемо обчислення:

=4,84 см.

або =0,735 рад.

Оскільки результуюче коливання є гармонічним, має ту саму частоту, що і складові коливання, то його можна записати у вигляді

,

де А = 4,84 см = 3,144 , = 0,735 рад.

Відповідь: , де А = 4,84 см = 3,144 , = 0,735 рад.

Приклад 15 На тонку гліцеринову плівку ( ) товщиною мкм нормально до її поверхні падає біле світло. Визначити довжини хвиль видимої ділянки спектра (0,4 0,8 мкм), які ослаблюються в результаті інтерференції.

Розв’язання. Оптична різниця ходу двох променів, відбитих від верхньої та нижньої поверхонь плівки, складає

. (61)

Щоб врахувати, що при відбиванні від пластинки виникає зміна фази на , додамо до правої частини співвідношення (61) :

. (62)

Умова спостереження інтерференційного мінімуму має вигляд

, (63)

де - порядок інтерференційного максимуму.

Прирівнявши вирази (62) і (63), знайдемо

. (64)

Після перетворень отримаємо

.

Звідси

, (65)

де може набувати значення

З цього виразу знайдемо _:

.

Після підстановки числових значень величин у співвідношення отримаємо:

,

м.

Оскільки – ціле число, одержимо остаточно , .

Тоді згідно з (65) відповідні довжини хвиль дорівнюють:

k	6	7	8	9	10	11
, мкм	0,735	0,63	0,557	0,49	0,441	0,401

Відповідь: м; м; м; м; м; м.

Приклад 16 На скляний клин з малим кутом нормально до його грані падає паралельний пучок проміння монохроматичного світла з довжиною хвилі = 0,6 мкм. Число m інтерференційних смуг, що при цьому виникає і припадає на відрізок клина довжиною l, дорівнює 10. Визначити кут клина.

Розв’язання. Паралельний промінь світла, що падає нормально до грані клина, відбивається як від верхньої, так і від нижньої грані. Ці відбиті промені світла когерентні. Тому на поверхні клина спостерігатимуться інтерференційні смуги. Оскільки кут клина малий, то відбиті промені 1 і 2 світла (рис.50) практично паралельні.

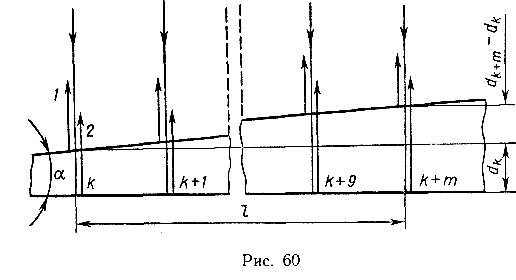
Рисунок 50 – Відбивання світла від клину

Темні смуги спостерігаються на тих ділянках клина, для яких різниця ходу променів кратна непарному числу половин довжини хвилі:

( = 0, ±1, ±2 ...). (66)

Різниця ходу двох хвиль складається з різниці оптичних довжин шляхів цих хвиль ( ) і половини довжини хвилі ( /2). Величина /2 є додатковою різницею ходу, що виникає при віддзеркаленні світлової хвилі 1 від оптично більш щільного середовища. Підставляючи у формулу (66) різницю ходу світлових хвиль, одержимо

, (67)

де n - показник заломлення скла (n =1,5); d_k - товщина клина в тому місці, де спостерігається темна смуга, що відповідає номеру ; - кут заломлення світла.

Згідно з умовою задачі кут падіння дорівнює нулю; отже, і кут заломлення дорівнює нулю, а тому, . Розкривши дужки в правій частині рівності (67), після спрощення отримаємо

. (68)

Нехай довільній темній смузі -го номера відповідає товщина d_k клина, а темній смузі k+m -го номера - товщина d_k+m клина. Тоді (рис.50), враховуючи, що m смуг укладається на відстані l, знайдемо:

. (69)

При малих кутах .

Виразимо з (68) d_k і d_k+m підставимо їх у співвідношення (69). Потім, враховуючи, що (через те, що кут малий), отримаємо

.

Підставляючи значення фізичних величин, знайдемо

.

Виразимо кут в секундах. Для цього можна скористатися співвідношеннями між радіаном і секундою: 1рад= = 20626 ~2,06 . Тоді = 210^-42,06 =41, .

Відповідь: = 210^-4 рад = 41, .

Приклад 17 Між скляною пластинкою і плосковипуклою лінзою, що лежить на ній, знаходиться рідина (рис.51). Знайти показник заломлення рідини, якщо радіус третього темного кільця Ньютона при спостереженні у відбитому світлі з довжиною хвилі дорівнює 0,82 мм. Радіус кривини лінзи 0,5 м.

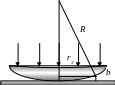
Рисунок 51 – Спостереження кілець Ньютона

Розв’язання. Схема установки спостереження кілець Ньютона зображена на рис. 51. З рисунка бачимо, що

, (70)

де – радіус кривини лінзи; – товщина зазору між лінзою і скляною пластинкою.

У виразі (70) ми знехтували величиною порівняно з . З цього співвідношення після простих перетворень отримаємо

. (71)

Оптична різниця ходу двох променів, відбитих від верхньої і нижньої поверхонь зазору між пластиною і лінзою, дорівнює

, (72)

де - коефіцієнт заломлення рідини у зазорі.

Щоб врахувати, що при відбитті від пластинки виникає зміна фази світла на , до правої частини виразу (72) додамо .

Умова спостереження інтерференційного мінімуму має вигляд

, (73)

де - порядок інтерференційного мінімуму.

Прирівнявши вирази (72) і (73), знайдемо

. (74)

Після перетворень отримаємо таке співвідношення:

.

З цього виразу знайдемо _:

. (75)

У випадку третього кільця Ньютона .

Після підстановки числових значень фізичних величин у (75) отримаємо

.

Відповідь: _.

Приклад 18 На поверхню дифракційної ґратки нормально до її поверхні падає монохроматичне світло. Стала дифракційної ґратки у =4,6 разу більша за довжину світлової хвилі. Знайти загальне число дифракційних максимумів, які теоретично можна спостерігати у цьому випадку.

Розв’язання. Умова спостереження дифракційного максимуму на дифракційній ґратці має вигляд

, (76)

де - порядок спектра, або у випадку монохроматичного світла порядок інтерференційного максимуму .

Останній інтерференційний максимум, який може спостерігатися при дифракції світла на ґратці, відповідає умові

.

Звідси отримаємо, що .

Тоді порядок дифракційного максимуму дорівнює

. (77)

Після підстановки числових значень величин у (77) отримаємо

.

Число обов’язково повинно бути цілим, але воно не може набувати значення 5, оскільки у цьому випадку , що неможливо. Звідси 4. Оскільки зліва і справа від центрального максимуму спостерігається однакова кількість максимумів, одержимо .

Відповідь: .

Приклад 19 Паралельний промінь світла переходить з гліцерину ( ) у скло ( ) так, що світло, відбите від межі цих середовищ, виявляється максимально поляризованим (рис.52). Визначити кут між падаючими та заломленими променями.

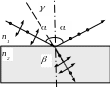
Рисунок 52 – Поляризація світла при відбиванні від межі поділу двох середовищ

Розв’язання. Згідно з законом Брюстера світло, відбите від межі поділу двох діелектриків, повністю поляризоване у тому випадку, якщо тангенс кута падіння дорівнює

, (78)

де – відносний показник заломлення середовищ; , – абсолютні показники заломлення середовищ.

Звідси

. (79)

Кут заломлення світла знайдемо із закону заломлення

. (80)

З виразу (80) маємо

або

. (81)

Кут , як бачимо з рисунка, дорівнює

. (82)

Підставивши значення у вирази (79), (81), (82), отримаємо

_.

.

.

Відповідь: _.

Приклад 20. У скільки разів ослаблюється інтенсивність світла, що проходить через два ніколі, площини пропускання яких утворюють кут , якщо у кожному ніколі окремо втрачається 10% інтенсивності світла, що падає на нього (рис.53).

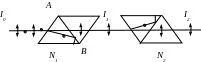
Рисунок 53 – Поляризація світла при проходженні через ніколі

Розв’язання. Промінь світла, що падає на грань ніколя N₁, розщеплюється внаслідок явища подвійного променезаломлення на два: звичайний і незвичайний. При цьому обидва промені мають однакову інтенсивність і повністю поляризовані. Площина коливань незвичайного променя лежить у площині креслення, у той час як для звичайного вона перпендикулярна до цієї площини.

Звичайний промінь внаслідок повного внутрішнього відбиття відбивається від межі АВ і через ніколь N₁ не проходить. Незвичайний промінь проходить через ніколь, при цьому інтенсивність світла зменшується вдвічі. Додаткове зменшення інтенсивності незвичайного променя відбувається внаслідок поглинання світла у речовині ніколя.

Таким чином, інтенсивність світла, що пройшло через ніколь N₁, дорівнює

, (83)

де - інтенсивність природного світла, що падає на ніколь N₁; - інтенсивність поляризованого світла, що пройшов через ніколь; k – коефіцієнт поглинання світла у ніколі.

Промінь плоскополяризованого світла інтенсивністю , що падає на ніколь N₂, теж розщеплюється на два промені: звичайний і незвичайний. При цьому звичайний промінь повністю поглинається в ніколі, а інтенсивність незвичайного променя, що виходить з ніколя, визначається законом Малюса

, (84)

де - кут між площиною коливань у поляризованому промені і площиною пропускання Ніколя N₂.

З урахуванням втрат енергії внаслідок поглинання світла у другому ніколі отримаємо

. (85)

Підставивши співвідношення (83) в (85), отримаємо

.

Звідси відношення інтенсивності світла на вході і виході з ніколей дорівнює

. (86)

Підставивши значення фізичних величин, знайдемо шукану величину

.

Відповідь: .

Задачі для самостійного розв’язання

1 По тонкому дроту, зігнутому у вигляді прямокутника, проходить струм силою = 60 А. Довжини сторін прямокутника дорівнюють а = 30 см і b = 40 см. Визначити магнітну індукцію В у точці перетину діагоналей прямокутника.

Відповідь: 200 мкТл.

2 Визначити індукцію магнітного поля в центрі дротяної квадратної рамки із стороною а = 15 см, якщо по рамці проходить струм I = 5 А.

Відповідь: 37,7 мкТл.

3 По тонкому дротяному півкільцю радіусом R = 50 см проходить струм I = 1 А. Перпендикулярно до площини півкільця збуджене однорідне магнітне поле з індукцією В = 0,01 Тл. Яка сила розтягує півкільце? Дію магнітного поля на дроти, що підводять струм до півкільця, і взаємодію окремих елементів півкільця не враховувати.

Відповідь: 0,01 Н.

4 По тонкому провіднику, зігнутому у формі правильного шестикутника із стороною =10 см, проходить струм силою А. Визначити магнітну індукцію у центрі шестикутника.

Відповідь: 138 мкТл.

5 Диск радіусом R = 8 см несе рівномірно розподілений по поверхні заряд ( = 100 нКл/м²). Визначити магнітний момент p_m, обумовлений обертанням диска відносно осі, що проходить через його центр і перпендикулярна до площини диска. Кутова швидкість обертання диска =60 рад/с.

Відповідь: 0,19 нАм².

6 Електрон в атомі водню рухається по коловій орбіті. Визначити відношення магнітного моменту р_т еквівалентного кругового струму до моменту імпульсу L орбітального руху електрона.

Відповідь: =87,8 ГКл/кг.

7 Напруженість магнітного поля в центрі кругового витка з магнітним моментом р_т = 1,5 Ам² дорівнює Н =150 А/м. Визначити: 1) радіус витка; 2) силу струму у витку.

Відповідь: 11,7 см; 35,1 А.

8 Круговий контур з дроту радіусом r = 5 см і струмом I = 1 А знаходиться в магнітному полі, причому площина контуру перпендикулярна до напряму поля. Напруженість поля дорівнює H=10 кА/м. Визначити роботу, яку необхідно виконати, щоб повернути контур на кут 90⁰ навколо осі, що співпадає з діаметром контуру.

Відповідь: 98,7 мкДж.

9 Альфа-частинка, що має швидкість =2 Мм/с, влітає під кутом = 30⁰ до однаково спрямованих магнітного (В = 1 мТл) і електричного (Е = 1 кВ/м) полів. Визначити прискорення -частинки в момент влітання у поле.

Відповідь: 6,8 10¹⁰ м/с².

10 Магнітне (В =2 мТл) і електричне (Е = 1,6 кВ/м) поля напрямлені однаково. Перпендикулярно до векторів і влітає електрон із швидкістю  = 0,8 Мм/с. Визначити прискорення а електрона в момент влітання у поля.

Відповідь: 4 10¹⁴ м/с.

11 Перпендикулярно до магнітного поля з індукцією В = =0,1 Тл збуджено електричне поле напруженістю Е = 100 кВ/м. Перпендикулярно до обох полів рухається, не відхиляючись від прямолінійної траєкторії, заряджена частинка. Визначити швидкість  частинки.

Відповідь:  = 1 Мм/с.

12 Електрон, що має швидкість = 1 Мм/с, влітає в однорідне магнітне поле під кутом а = 60⁰ до напряму поля і починає рухатися по гвинтовій лінії. Напруженість магнітного поля Н = 1,5 кА/м. Визначити: 1) крок гвинтової лінії; 2) її радіус.

Відповідь: 9,49 мм; 2,62мм.

13 На картонний каркас довжиною l = 50 см і площею перерізу, що дорівнює S=4 см², намотаний в один шар дріт діаметром d = 0,2 мм так, що витки щільно прилягають один до одного (товщиною ізоляції знехтувати). Обчислити індуктивність L одержаного соленоїда.

Відповідь: L=6,28 Гн.

14 В однорідному магнітному полі (В=0,1 Тл) рівномірно з частотою =5 с^-1 обертається стрижень довжиною l=50 см так, що площина його обертання перпендикулярна до ліній напруженості, а вісь обертання проходить через один з його кінців. Визначити індуковану на кінцях стрижня різницю потенціалів U.

Відповідь: U=0,39 В.

15 Рамка площею S= 200 см² рівномірно обертається з частотою = 10 с^-1 відносно осі, що лежить в площині рамки і перпендикулярна до ліній індукції однорідного магнітного поля (В =0,2 Тл). Яке середнє значення ЕРС індукції < > за час, протягом якого магнітний потік, що пронизує рамку, зміниться від нуля до максимального значення?

Відповідь: =0,16 В.

16 Магнітна індукція поля між полюсами двополюсного генератора дорівнює В=1 Тл. Ротор має 140 витків (площа кожного витка S = 500 см²). Визначити частоту обертання якоря, якщо максимальне значення ЕРС індукції дорівнює 220 В.

Відповідь: 5 с^-1.

17 Коливання матеріальної точки масою m = 0,1 г відбуваються відповідно до рівнянь х=A cost де А = 5 см, =20 с^-1. Визначити максимальні значення повертаючої сили F_max і кінетичної енергії E_max.

Відповідь: F_max=2 мН; E_max. =50 мкДж.

18 Гиря, підвішена до пружини, коливається по вертикалі з амплітудою А = 4 см. Визначити повну енергію Е коливань гирі, якщо жорсткість пружини дорівнює k=1 кН/м.

Відповідь: 0,8 Дж.

19 Рух точки заданий рівняннями: і _, де А₁=10 см; А₂=5 см; =2 с^-1, =/4 с. Знай-ти рівняння траєкторії і швидкість точки у момент часу t= 0,5 с.

Відповідь: ; 13,7 м/с.

20 Складаються два гармонічних коливання одного напрямку з однаковими періодами Т₁ = Т₂ = 1,5 с і амплітудами А₁ = А₂ = 2 см. Початкові фази коливань = /2, = /3. Визначити амплітуду А і початкову фазу результуючого коливання. Знайти його рівняння і побудувати з дотриманням масштабу векторну діаграму додавання амплітуд.

Відповідь: 3,86 см; 0,417 рад; 4,19 с^-1; .

21 Амплітуда затухаючих коливань маятника за 120 с зменшилась в 2 рази. Визначити коефіцієнт затухання.

Відповідь: 5,78·10^-3 с^-1.

22 Тіло масою 0,6 кг, підвішене на спіральній пружині з жорсткістю 30 Н/м, здійснює в деякому середовищі пружні коливання. Логарифмічний декремент затухання 0,01. Визначити: час, за який амплітуда коливань зменшиться в три рази; число повних коливань, які повинно здійснити тіло, щоб відбулося дане зменшення амплітуди.

Відповідь: 97,6 с; 110.

23 При спостереженні затухаючих коливань з'ясувалося, що для двох послідовних коливань амплітуда другого менше амплітуди першого на 60%. Період затухаючих коливань Т = =0,5 с. Визначити: 1) коефіцієнт загасання ; 2) частоту незагасаючих коливань.

Відповідь: = 1,83 с^-1; 2) = 2,02 Гц.

24 Гиря масою т = 0,5 кг, підвішена на спіральній пружині жорсткістю k = 50 Н/м, здійснює коливання у в'язкому середовищі з коефіцієнтом опору r = 0,5 кг/с. На верхній кінець пружини діє змушувальна сила, що змінюється за законом , H. Визначити для даної коливальної системи: 1) коефіцієнт загасання ; 2) резонансну амплітуду А_рез

Відповідь: =0,5 с^-1; А_рез =2 см.

25 Плоска гармонічна хвиля з періодом =0,25 с і амплітудою =3 см поширюється зі швидкістю =240 м/с. Чому дорівнює зміщення точки, що міститься на відстані =60 м від джерела тоді, коли від початку коливань джерела пройшов час 1,5 с? Початкова фаза хвилі дорівнює нулю.

Відповідь: 3 см.

26 У скільки разів швидкість повздовжньої хвилі в міді більша, ніж швидкість поперечної хвилі? Модуль зсуву для міді =44 ГПа, а модуль Юнга ГПа?

Відповідь: У 1,49 разу.

27 У стальному стрижні діаметра =1 см поширюється повздовжня хвиля де =10^-4 см, = мс. Визначити максимальну силу, що діє в перерізі стрижня.

Відповідь: F=3,11 H.

28 Визначити швидкість звуку при нормальних умовах у : 1) гелії; 2) азоті; 3) вуглекислому газі.

Відповідь: 972 м/с; 337 м/с; 262 м/с.

29 Відстань між двома щілинами в досліді Юнга d = =0,5 мм ( = 0,6 мкм). Визначити відстань L від щілин до екрана, якщо ширина інтерференційних смуг дорівнює =1,2 мм.

Відповідь: 1 м.

30 На скляний клин (п=1,5) нормально падає монохроматичне світло ( =698 нм). Визначити кут між поверхнями клина, якщо відстань між двома сусідніми інтер-ференційними мінімумами у відбитому світлі дорівнює 2 мм.

Відповідь: 24".

31 Плоско-опукла лінза радіусом кривини 4 м опуклою стороною лежить на скляній пластинці. Визначити довжину хвилі падаючого монохроматичного світла, якщо радіус п'ятого світлого кільця у відбитому світлі дорівнює 3 мм.

Відповідь: 0,5 мкм.

32 На лінзу з показником заломлення п = 1,58 нормально падає монохроматичне світло з довжиною хвилі  = 0,55 мкм. Для усунення втрат світла в результаті відбивання на лінзу наноситься тонка плівка. Визначити: 1) оптимальний коефіцієнт заломлення для плівки; 2) тов-щину плівки.

Відповідь: 1,26; 109 нм.

33 При освітленні дифракційної ґратки білим світлом спектри другого і третього порядків частково перекривають один одного. На яку довжину хвилі в спектрі другого порядку накладається фіолетова межа ( = 0,4 мкм) спектра третього порядку?

Відповідь: 0,6 мкм.

34 На дифракційну гратку нормально падає монохроматичне світло з довжиною хвилі = 600 нм. Визначити найбільший порядок спектра, одержаний за допомогою цієї ґратки, якщо її стала d = 2 мкм.

Відповідь: 3.

35 На дифракційну ґратку довжиною l = 1,5 мм, що містить N = 3000 штрихів, падає за нормаллю монохроматичне світло з довжиною хвилі = 550 нм. Визначити: 1) число максимумів, щo спостерігаються в спектрі цієї ґратки; 2) кут, що відповідає останньому максимуму.

Відповідь: 18; 81⁰54'.

36 Монохроматичне світло нормально падає на дифракційну ґратку. Визначити кут дифракції, що відповідає максимуму четвертого порядку, якщо максимум третього порядку відхилений на ₃ = 18⁰.

Відповідь: 24⁰20'.

37 Визначити ступінь поляризації Р суміші природного світла з плоскополяризованим, якщо інтенсивність поляризованого світла дорівнює інтенсивності природного.

Відповідь: 0,5.

38 Інтенсивність природного світла, що пройшло через два ніколі, зменшилася у 8 разів. Нехтуючи поглинанням світла, визначити кут між площинами пропускання ніколів.

Відповідь: 60⁰.

39 Визначити, під яким кутом до горизонту має знаходитися Сонце, щоб промені, відбиті від поверхні озера ( = 1,33), були максимально поляризовані.

Відповідь: 36⁰56'.

40 Світло, що проходить через рідину, налиту в скляну посудину (п = 1,5), відбивається від дна, причому відбите світло плоскополяризоване при падінні його на дно посудини під кутом 41⁰. Визначити: 1) показник заломлення рідини; 2) кут падіння світла на дно посудини, при якому спостерігається повне відбиття.

Відповідь: 1,73; 60⁰7'.