9. Задача анализа сложности алгоритмов. Временная и емкостная сложности. Оценки сложности. Использование управляющего графа для оценки сложности линейных и ветвящихся алгоритмов.

Сложность алгоритма определяется в двух аспектах: сложность по памяти и сложность по времени исполнения. Емкостная сложность алгоритма определяет, насколько много памяти требуется для выполнения этого алгоритма. Временная сложность алгоритма определяет, насколько много процессорного времени требует алгоритм для своего выполнения.

Оценка временной сложности. Рассчитывается в относительных единицах так, чтобы эта оценка, по возможности, была одинаковой для компьютеров с разной тактовой частотой, а именно в количестве исполняемых операций. Рассмотрим подробно список операций, учитываемых при подсчете временной сложности (каждая из перечисленных операций принимается с весом равным 1)

• арифметические операции (+,–,*,/,div, mod);

• унарный минус (–);

• операция пересылки, возникающая при выполнении оператора присваивания (:=);

• операции сравнения (>,<,=,<=,>=,<>);

• логические и побитовые операции (not, and, or, xor, shr, shl);

• выполнение стандартных функций (inc(), dec(), abs(), sin(), cos(), exp(), ln(), arctan(), sqr(), sqrt(), int(), frac(), round(), trunc(), odd(), chr(), ord(), pred(), succ(), upcase(), high(), low());

• операции ввода-вывода одной переменной (read(), readln(), write(), writeln()).

Оценка емкостной сложности. Учет памяти обычно ведётся по объёму данных и не принимается во внимание память, расходуемая для записи команд программы. Обозначим емкостную сложность алгоритма  через S_. Емкостную сложность будем подсчитывать в относительных единицах, не зависящих от языка программирования и компьютера на котором происходит выполнение программы, а именно в количестве скалярных переменных, описанных в программе. Под скалярными переменными будем понимать переменные и константы простых (скалярных) типов данных. Напомним, что к простым (скалярным) типам данных в Паскале относятся:

• все числовые типы (целые – Integer, Byte, Word, ShortInt, LongInt;

вещественные – Real, Single, Double, Extended);

• символьный тип (Char);

• логический тип (Boolean);

• перечислимый тип;

• интервальный тип.

• массив

емкостная сложность определяется числом элементов массива

• строковый тип

емкостная сложность на единицу больше числа символов максимально допустимых в строке

• запись

емкостная сложность равна сумме емкостных сложностей полей записи

Для многих задач возможно найти только верхнюю (T_max) или нижнюю (T_min) оценку сложности алгоритма, а также среднюю (T_average) оценку. Для нахождения верхней оценки оценивается количество необходимых операций в худшем случае, то есть для набора исходных данных, требующих максимального количества операций обработки. Для нахождения нижней оценки ищется сложность для набора данных, требующего минимального количества операций.

Отыскание функции сложности производится на основе анализа текста алгоритма. С целью анализа алгоритм удобно представлять управляющим графом. В нём каждому оператору или вызову процедуры ставится в соответствие вершина графа (точка).

Каждой вершине графа припишем число – количество операций, которые необходимо выполнить для исполнения оператора программы, связанного с этой вершиной. Это число назовём весом вершины. Вес пустой, начальной и заключительных вершин равен 0.

1. Управляющий граф представляет собой линейный участок. Сложность равна сумме весов вершин, принадлежащих линейному участку. Если на участке нет вершин – вызовов процедур, то сложность является константой.

Пример:

Рассмотрим фрагмент алгоритма:

a:=y+r;

Proc(a,y);

b:=4*d – 10 mod b;

Известно, что сложность процедуры Proc равна 2V+1.

Построим управляющий граф, снизу от каждой вершины графа напишем ее вес.

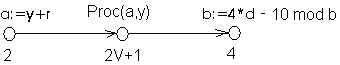
T_(V)=2V+7.

2. Управляющий граф содержит разветвления, но не содержит циклов. Расчёт сложности зависит от того, рассматриваем мы худший, лучший или средний случай.

Поскольку для вычисления средней оценки сложности используется вероятностный подход, приведем начальные понятия из теории вероятности:

• Вероятность события (p) есть объективная мера возможности события, выражаемая числом, удовлетворяющим условию 0 ≤ p ≤ 1.

• Достоверное событие, т.е. то событие, которое непременно произойдет, имеет вероятность равную 1.

• Невозможное событие имеет вероятность равную 0.

Пример:

Рассмотрим фрагмент алгоритма:

If a<b then x:=a else x:=b-2;

Известно, что вероятность выполнения условия a<b равна .

Построим управляющий граф, внутри каждой вершины графа напишем ее вес.

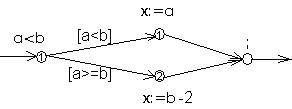
Вычислим веса ветвей T₁ = 1+1+0 = 2, T₂ = 1+2+0 = 3. T_min = 2, T_max = 3. Для определения средней оценки сложности вычислим вероятности выполнения ветвей.

p₁ = по условию,

p₂ = 1 – p₁ = , т.к. события «выполнилась 1 ветвь» и «выполнилась 2 ветвь» несовместны и образуют полную группу.

T_average = p₁T₁+p₂T₂ = ·2+ ·3 = 2 = 2,25.