4. Вычислимые функции. Базовый набор функций и операции над функциями: суперпозиция, примитивная рекурсия, минимизация. Классы вычислимых функций. Примеры.

Вычислимая функция – функция, для которой можно построить некоторый алгоритм.

1. Определим базовый набор функций, для которых уже построена машина Тьюринга.

Предположим, что все функции преобразуют целые числа в целые числа.

- функция обнуления

- функция суммы

- функция выбора. Выбирает из набора аргументов аргумент с номером

Обозначим этот базовый набор за

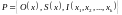
2. В базовом наборе функций определим основные операции. Операции получают функции (а не значения функций) в качестве операндов и дают в результате новые функции. Эти операции также должны быть очевидны с математической точки зрения – не должно возникать сомнения в том, что из вычислимых функций с помощью операций получаются вновь вычислимые функции. Последовательно применяя операции к множеству функций из мы будем получать новые функции, которые будут расширять набор . Следовательно, мы сможем построить бесконечный набор функций.

Обозначим набор этих операций . в систему операций входят три операции: суперпозиция , примитивная рекурсия и минимизация .

Суперпозиция

Будем предполагать, что все функции, к которым применяется операция суперпозиции, определены на одном и том же наборе входных данных. Обозначим функции, к которым применяется операция суперпозиции:

Если какой-то элемент из набора не используется для вычисления какой-то из функций, то для этой функции мы объявляем этот элемент не значащим.

Входными данными для будут результаты вычисления 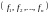для набора

, где - количество переменных в объединенном наборе переменных функций с индексами от 1 до .

Все рассматриваемые функции являются частными, т.е не всюду определенными; могут существовать такие комбинации аргументов, для которых значение функции не существует.

Функция не будет определена в двух случаях:

1. Значение не определено

2. , но при этом не определено

Примитивная рекурсия

Операция примитивной рекурсии имеет два операнда

Первый операнд, функция , зависит от аргументов, , а второй операнд, функция h, в общем случае имеет два дополнительных аргумента. Функция – результат f определяется следующими уравнениями примитивной рекурсии:

Операция минимизации

Операция минимизации μ имеет один операнд, f=μ(g). Значения функции f на заданном наборе аргументов x₁…x_n получаются следующим образом. Сначала с помощью функции g формируется уравнение , а затем отыскивается его решение y. Если таких решений несколько, то берется минимальное из них; оно и считается значением функции f на данном наборе аргументов. Может случится, что уравнение не имеет ни одного решения. В этом случае считается, что функция f не определена на заданном наборе аргументов.

Примеры определения функций при помощи этих трех операций:

1)

2)

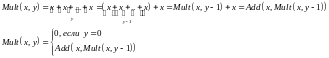
3)

Классы вычислимых функций

Множество всех функций которые можно получить из базового набора с помощью операций суперпозиции и примитивной рекурсии, называется примитивно рекурсивными функциями . Все примитивно рекурсивные функции всюду вычислимы. Для того чтобы расширить набор следовало бы, кроме примитивной рекурсии ввести еще и кратную рекурсию, определить косвенную рекурсию.

P_р – класс общерекурсивных функций. Образует множество всюду определенных вычислимых функций.

Оператор минимизации может превратить всюду определенную функцию в частичную.

Множество функций, получаемых применением к базовому набору конечного числа операций типа суперпозиции, примитивной рекурсии и минимизации называется множеством частично-рекурсивных функций и обозначается .

Р_выч – множество всех вычислимых функций. Замкнуто относительно операций суперпозиции, примитивной рекурсии и минимизации.

Тезис Чёрча: числовая функция тогда и только тогда алгоритмически выполнима, когда она частично рекурсивна