
- •Понятие алгоритма и свойства алгоритмов.
- •Формализация понятия алгоритма: машина Тьюринга. Представление машин Тьюринга с помощью диаграмм. Табличное представление программ машины Тьюринга. Композиция машин Тьюринга. Примеры.
- •Двумерная таблица
- •С помощью диаграммы
- •Формализация понятия алгоритма: нормальные алгорифмы Маркова, определение и выполнение. Примеры.
- •Вычислимые функции. Базовый набор функций и операции над функциями: суперпозиция, примитивная рекурсия, минимизация. Классы вычислимых функций. Примеры.
- •Проблема алгоритмической разрешимости. Примеры неразрешимых алгоритмических проблем.
- •Методы разработки алгоритмов. Суперпозиция, итерация, рекурсия и др.
- •Технология разработки программ. Технология и методы тестирования программ.
- •Составление алгоритма.
- •Создание документации, помощи.
- •Рекурсивные алгоритмы: определение и виды рекурсии. Реализация рекурсии и использование стека. Рекурсия и итерация. Примеры, сравнение.
- •Задача анализа сложности алгоритмов. Временная и емкостная сложности. Оценки сложности. Использование управляющего графа для оценки сложности линейных и ветвящихся алгоритмов.
- •Оценка сложности циклических алгоритмов. Примеры.
- •Количество повторений вложенного цикла не зависит от параметра внешнего цикла
- •Количество повторений вложенного цикла зависит от параметра внешнего цикла
- •Оценка сложности рекурсивных алгоритмов: рекурсия с одним и многими рекурсивными вызовами, случай косвенной рекурсии.
- •If … then процедура_1
- •Оптимизация алгоритмов. Примеры.
- •Понятие сложности задачи и классы сложности задач. Понятие сводимости, полиномиальная сводимость.
- •Методы сортировок: сортировка массивов простыми включениями, сортировка массивов простым выбором, сортировка обменами. Анализ сложности алгоритмов сортировки.
- •Сортировка методом простого выбора
- •Сортировка методом простых вставок (метод прямого (простого) включения)
- •2 Пересылки записей
- •1 Пересылка записи
- •Методы сортировок: алгоритм быстрой сортировки. Анализ сложности алгоритма быстрой сортировки.
- •Обзор методов сортировок: сортировка Шелла, пирамидальная сортировка, сортировка слияниями, Шейкер-сортировка, сортировка подсчетом, цифровая сортировка и др.
- •Методы поиска: линейный поиск, метод бинарного поиска, поиск с помощью бинарного дерева, метод случайного поиска и др.
- •Алгоритмы внешней сортировки: метод естественного слияния, метод сбалансированного слияния. Двухпутевая и многопутевая реализации. Фибоначчиева сортировка.
- •Метод квадратичного рехеширования.
- •Рекурсивные типы данных: определение, примеры.
- •Id:integer; {номер вершины}
- •Операции над линейными списками: создание списков, включение элементов в списки (рассмотреть различные способы). Виды связных списков.
- •Операции над линейными списками: удаление элементов списков. Поиск элементов списков, сравнение списков.
- •Операции над бинарными деревьями: включение вершины в дерево. Обход деревьев, подсчет числа вершин в дереве. Подсчет числа вершин, удовлетворяющих заданному условию.
- •Операции над бинарными деревьями: удаление вершины дерева.
- •Понятие сбалансированности бинарного дерева. Приведение дерева к авл-сбалансированному виду: виды и формулы поворотов.
- •Анализ сложности алгоритмов работы с бинарными деревьями.
- •Деревья со многими потомками. Специальные виды деревьев: деревья формул, б-деревья, 2-3 деревья, красно-черные деревья.
- •Понятие графа. Способы представления графов. Операции над графами: добавление вершины, добавление дуги, создание графа.
- •Операции над графами: поиск вершины, удаление вершины, удаление дуги, текстовый вывод графа.
- •Алгоритмы поиска на графах: поиск в глубину и в ширину.
- •Примеры алгоритмов на графах (поиск кратчайшего пути, поиск циклов, алгоритм построения остовного дерева, выделения связных компонентов…).
- •Формальные языки и грамматики. Определение языка, описание языка. Понятие грамматики.
- •Классификация формальных языков. Понятие вывода.
- •Описание синтаксиса языка с помощью синтаксических диаграмм и бнф. Примеры.
- •Основы теории информации. Понятие энтропии. Измерение информации: вероятностный и алфавитный подходы.
- •Основы теории кодирования информации. Метод Шеннона-Фано. Код Хаффмана.
- •1. Принцип программного управления.
- •2. Принцип однородности памяти.
- •3. Принцип адресности.
- •Конвейеризация вычислений.
- •Иерархия запоминающих устройств эвм
- •Устройство процессора. Понятие архитектуры cisc, risc, vliw.
- •Работа процессора
- •Cisc-процессоры
- •Risc-процессоры
- •Misc-процессоры
- •Vliw-процессоры
- •Типы данных, поддерживаемые процессорами Intel, форматы данных.
- •Система команд Intel, классификация команд, форматы команд.
- •Объектно-ориентированное программирование (ооп): основные понятия.
Формализация понятия алгоритма: нормальные алгорифмы Маркова, определение и выполнение. Примеры.
Алгорифмы Маркова (нормальные алгорифмы) используются для представления алгоритмов, преобразующих одну цепочку символов (исходные данные) в другую (результат).
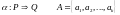
Отличие алгорифмом Маркова в том, что каждый шаг преобразования позволяет выполнить замену не одного символа, а целого слова в исходной цепочке.
Если применив алгоритм
 к строке
к строке
 ,
мы, за конечное число шагов, получили
результат
,
мы, за конечное число шагов, получили
результат
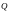 ,
то такой алгоритм будем называть
применимым и обозначать
,
то такой алгоритм будем называть
применимым и обозначать

Замены выполняются в соответствии с заданным правилом, которые и будут определять алгоритм. Такой алгоритм называется вербальным.
Расширим алфавит
 тремя символами «
тремя символами «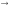 »,
«
»,
« ».
«|». Предполагается, что в алфавит
эти символы не входят. В расширенном
алфавите можно записывать разные слова,
но особенное внимание уделим словам
вида:
».
«|». Предполагается, что в алфавит
эти символы не входят. В расширенном
алфавите можно записывать разные слова,
но особенное внимание уделим словам
вида:
 ,
где
,
где
 - один из двух символов: стрелка или
стрелка с точкой,
- один из двух символов: стрелка или
стрелка с точкой,
 - любая цепочка символов в алфавите
.
- любая цепочка символов в алфавите
.
Если такое правило срабатывает, то в
исходной строке отыскивается подстрока
 и она целиком заменяется на
и она целиком заменяется на
 .
.
Для определения алгоритма нужно задать
не одно правило, не одну формулу
подстановки, а множество, причем
необходимо определить порядок их
применения. Для этого вводится еще одно
понятие схемы алгоритма. Схемой –
называется слово в расширенном алфавите,
имеющее вид
 ,
где
,
где
 - формулы подстановок. Чем меньше номер,
тем выше приоритет. Это значит, что если
в цепочке символов, которая преобразуется
с помощью алгоритма, встречается
несколько подстрок, то применяться
будет формула, имеющая минимальный
номер.
- формулы подстановок. Чем меньше номер,
тем выше приоритет. Это значит, что если
в цепочке символов, которая преобразуется
с помощью алгоритма, встречается
несколько подстрок, то применяться
будет формула, имеющая минимальный
номер.
Если в строке, которая преобразуется алгорифмом встречается левая часть какой-то формулы , то это означает, что формула - действует на эту строку. В общем случае в схеме может быть несколько формул, которые действуют на строку, но выбираться будет с большим приоритетом.
Если какая-то подстановка действует на исходную строку, причем левая часть встречается в строчке многократно, то формула подстановки применяется один раз. Причем применяется к самому левому вхождению.
При заменах могут использоваться пустые строки

Если в схеме используется несколько правил, в которых правые части совпадают, а левые части являются подстроками, которые можно объединить в какое-то множество, то пишут
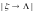 ,
где
- все элементы от А до Я
,
где
- все элементы от А до Я
Пустая строка может встречаться и в левой части. Если есть такие правила, то пустота заменится слева. В этом случае при составлении схемы нужно думать о том, чтобы алгоритм был применим.
Каким образом алгоритм завершает работу?
Есть несколько вариантов:
1. Не применима ни одна подстановка в схеме (не действует на полученную строку)
2. Выбирается формула подстановки вида:
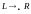 .
Такая формула подстановки называется
заключительной. После ее применения
алгоритм завершает работу. Если в левой
части этой формулы используется пустая
стока, то эта формула подстановки не
должна иметь высокий приоритет и
обязательно должна присутствовать
заключительная формула с большим
приоритетом.
.
Такая формула подстановки называется
заключительной. После ее применения
алгоритм завершает работу. Если в левой
части этой формулы используется пустая
стока, то эта формула подстановки не
должна иметь высокий приоритет и
обязательно должна присутствовать
заключительная формула с большим
приоритетом.
