Двумерная таблица
Для начала выполнения программы определяется начальная (стартовая) конфигурация машины Тьюринга. Нормальная конфигурация – головка установлена на самый левый не пустой символ.
Выполнение алгоритма прекращается, когда на пересечении строки соответствующей текущему считываемому символу и столбца соответствующего текущему состоянию оказывается пустая ячейка.
Пример:
-
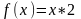
Q
A
q1
q2
q3
0
0 q1 R
0 q2 L
1
1 q1 R
1 q2 L
e
0 q2 L
e q3 R
С помощью диаграммы
Д
иаграмма
представляет собой геометрический
объект (ориентированный граф), состоящий
из вершин и дуг. Каждой вершине
приписывается состояние машины Тьюринга:
таким образом, вершин в диаграмме ровно
столько, сколько имеется состояний.
Дуге, соединяющей две вершины qi
и qj,
приписывается некоторый символ a
алфавита A и двойка b
D так, что запись
a qi
b qj
D образует
команду программы машины Тьюринга.
Композиция машин Тьюринга
Машины должны работать в одном алфавите и множества их состояний не должны пересекаться.
Последовательное соединение машин.
Для организации такой работы достаточно построить объединенную таблицу машины Тьюринга, приписав к первой таблице вторую (справа) и заполнив пустые клетки первой таблицы командой перехода к начальному состоянию второй программы.
f(x)=(x+1)*2
-
g1
g2
g3
g4
s1
s2
s3
1 g1 R
0 g2 L
1 g3 L
1 s1 S
1 s1 R
1 s2 L
0
0 g1 R
1 g3 L
0 g3 L
0 s1 S
0 s1 R
0 s2 L
e
e g2 L
1 g4 S
e g4 R
0 s2 L
e s3 R
Итерация (повторение) машин Тьюринга
В этом случае повторяем выполнение одной и той же команды конечное число раз. По окончании первого выполнения на ленте остается промежуточный результат необходимый для второго выполнения и т.д. Для обеспечения второго и последующих выполнений необходимо в некоторые пустые клетки таблицы вписать команду перехода на начало. Во все пустые клетки эту команду вписывать нельзя, так как измененная таким образом программа не сможет заканчиваться.
f(X)=X+L eeeeX*Leeeee
|
s1 |
s2 |
q1 |
q2 |
q3 |
q4 |
q5 |
1 |
1 s1 L |
1 q1 S |
1 q1 R |
e q3 L |
1 q3 L |
1 q4 L |
|
e |
1 s2 S |
|
e q2 L |
|
e s1 R |
e q5 R |
|
* |
|
|
* q1 R |
|
* q3 L |
|
|