Алгоритмы поиска на графах: поиск в глубину и в ширину.
Поиск в глубину.
Обход в глубину (называемый иногда стандартным обходом), есть обход графа по следующим правилам:
1. Добавляет начальную вершину в стек и помечает еѐ как использованную.
2. Рассматривает верхнюю вершину стека и добавляет в стек первую попавшуюся смежную ей неиспользованную вершину, помечая еѐ как использованную. Если такой вершины нет,
извлекает вершину стека.
3. Если стек не пуст, переходит к пункту 2. 3
Таким образом, этот алгоритм обходит все вершины, достижимые из начальной, и каждую вершину обрабатывает не более одного раза.
Текст процедуры обхода в глубину (рекурсивный вариант):
var a:array[1..nmax,1..nmax]of integer;// матрица смежности
used:array[1..nmax]of boolean; // список меток
data:array[1..nmax] of integer; //информационные поля вершин
n:integer; // количество вершин графа
procedure dfs(v:integer; search:ineger);
var
i:integer;
begin
used[v]:=true; // помещенная в стек вершина помечается использованной
for i:=1 to n do // рассматриваются все ребра, исходящие из этой вершины
// проверка, использована ли вершина, в которую ведет выбранное ребро, если да, то поиск продолжается из этой вершины.
if (a[v,i]=1)and(not used[i]) then
begin
if data[i]=search then write('Вершина с индексом ',i)
else
dfs(i,search);
end;
end;
...
dfs(X,k); // здесь X - номер начальной вершины, k- информационное поле вершины.
Поиск в ширину.
Обход графа в ширину (breadth first search, BFS) основывается на замене стека очередью:
1. Добавляет начальную вершину в очередь и помечает еѐ как использованную.
2. Извлекает следующую вершину из очереди и добавляет в очередь смежные ей неиспользованные вершины, помечая их как использованные.
3. Если очередь не пуста, переходит к пункту 2.
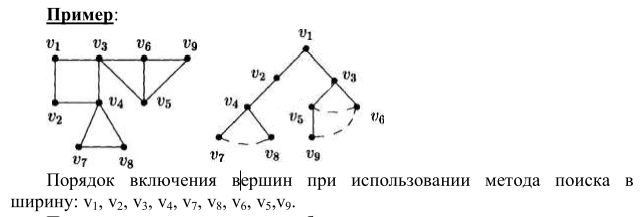
Писать поиск в ширину, как и большинство других алгоритмов, лучше для графа, заданного списком рѐбер. В этом случае алгоритм более мобилен (это важно при модификациях) и даѐт оптимальное время работы.
procedure bfs(v:integer);
var Og:array[1..nn]of integer;
yk1,yk2:integer;
i:integer;
begin
// в элементе og[i] хранится номер группы вершины i.
Изначально номер группы всех вершин кроме стартовой равен 0, это
значит, что они ещѐ не были использованы.
for i:=1 to n do
og[i]:=0;
// Инициализация очереди, т.е. добавление в неѐ начальной
вершины с номером v
yk2:=0;
yk1:=1;
Og[yk1]:=v;
used[v]:=true; // пометка вершины использованной
while yk2 < yk1 do // цикл работает, пока очередь не пуста
begin
inc(yk2);v:=Og[yk2];
write(v:2);
// просматриваются все рѐбра, исходящие из первой вершины
очереди
for i:=1 to n do
// использована ли вершина, в которую ведѐт выбранное ребро,
если нет , то вершина добавляется в очередь
if (a[v,i] <> 0) and not used[i] then
begin
// сдвигается указатель конца очереди
inc(yk1);
Og[yk1]:=i;
used[i]:=true;
end;
end;
end;