Анализ сложности алгоритмов работы с бинарными деревьями.
????
Деревья со многими потомками. Специальные виды деревьев: деревья формул, б-деревья, 2-3 деревья, красно-черные деревья.
Деревья со многими потомками:
У таких деревьев от вершины может быть сколько угодно потомков. Возможный тип представления:
type refnode=^node
node = record
inf:integer;
a1:refnode;
a2:refnode;
a3:refnode;
...
an:refnode;
end;
Деревья формул:
Дерево-формула это бинарное дерево, построенное из строки, в которой записано какое-то алгебраическое выражение.
Пример такого дерева:
В каждом его листе хранится либо переменная, либо число, а во всех остальных вершинах, которые не являются листами могут хранится арифметические операции.
Описание типа:
Type pnode=^node;
Node=record
data: string;
Left, right, parent: pnode
End;
Б – деревья
Структура данных, дерево поиска. С точки зрения внешнего логического представления, сбалансированное, сильно ветвистое дерево во внешней памяти.
Сбалансированность означает, что длина любых двух путей от корня до листов различается не более, чем на единицу.
Ветвистость дерева — это свойство каждого узла дерева ссылаться на большое число узлов-потомков.
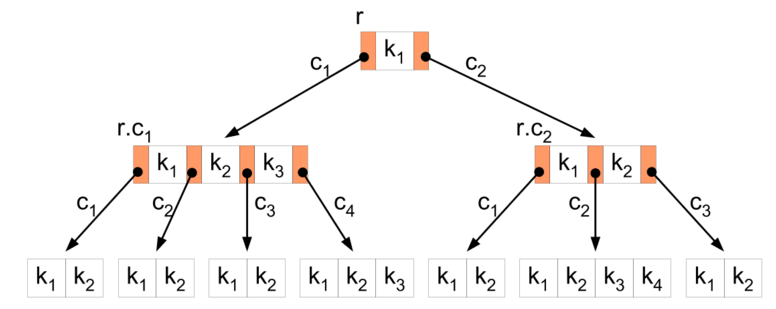
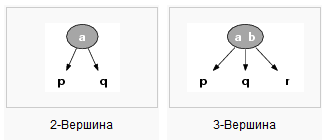
2-3 деревья
Структура данных являющаяся B-деревом Степени 1, Страницы которого могут содержать только 2-вершины (вершины с одним полем и 2-мя детьми) и 3-вершины (вершины с 2-мя полями и 3-мя детьми). Листовые вершины являются исключением — у них нет детей (но может быть одно или два поля). 2-3 деревья сбалансированы, то есть каждое левое, правое, и центральное поддерево одинаковой высоты, и таким образом содержат равное (или почти равное) число данных.
Красно – черные деревья
Это одно из самобалансирующихся двоичных деревьев поиска, гарантирующих логарифмический рост высоты дерева от числа узлов и быстро выполняющее основные операции дерева поиска: добавление, удаление и поиск узла. Сбалансированность достигается за счёт введения дополнительного атрибута узла дерева — «цвета». Этот атрибут может принимать одно из двух возможных значений — «чёрный» или «красный»
Узел либо красный, либо черный.
Корень — черный. (В других определениях это правило иногда опускается. Это правило слабо влияет на анализ, так как корень всегда может быть изменен с красного на черный, но не обязательно наоборот).
Все листья — черные.
Оба потомка каждого красного узла — черные.
Всякий простой путь от данного узла до любого листового узла, содержит одинаковое число черных узлов.
Понятие графа. Способы представления графов. Операции над графами: добавление вершины, добавление дуги, создание графа.
Граф (graph) – объект, состоящий из множества кружков (точек) и множество соединяющих их линий. Кружки (точки) называются вершинами графа (nodes), линии со стрелками – дугами (arcs), без стрелок – ребрами.
Граф, в котором направление линий не выделяется (все линии являются ребрами), называется неориентированным
Граф, в котором направление линий принципиально (линии являются дугами) называется ориентированным (орграф).
Способы представления графов в памяти
Матрица смежности – это матрица n×n, где n - число вершин. Строка с номером i содержит 1 в строке с номером j, если существует дуга из вершины i в вершину j.
Матрица инцидентности
Матрица инцидентности имеет размер m*n, где n – количество вершин, m – количество дуг графа. Элемент матрицы, соответствующий k-дуге и i-ой вершине, равен
+1, если дуга выходит из вершины;
–1, если дуга входит в вершину
и нули во всех остальных строках.
Списки смежности
Этот способ задания графов подразумевает, что для каждой вершины будет указан список всех смежных с нею вершин
Этот способ представления графов является внутренней реализацией
списка смежности: в одном линейном списке содержатся номера начальных
вершин, а в остальных – списки исходящих из них дуг. Введем следующие
типы данных для представления графов:
Type refnode=^node;
refarc=^arc;
node=record {список вершин}
id:integer; {номер вершины}
infnode:integer; {вес}
next:refnode; {указатель на следующую вершину в
списке}
arclist:refarc {указатель на список дуг}
end;
arc=record {список дуг определенной вершины}
infarc:integer; {вес}
next:refarc; {указатель на следующую дугу, исходящую из
данной вершины}
adj :refnode {указатель на вершину, в которую ведет данная
дуга}
end;
Добавление вершины
Процедура AddNode добавляет в граф вершину с заданным номером n и весом x. Предполагается, что уникальность номера обеспечивается вызывающей программой.
Procedure AddNode(Var graph: refnode; n,x:integer);
Var p:refnode;
Begin new(p);
With p^ do
Begin id:=n;
Infnode:=x;
Arclist:=nil;
Next:graph
End;
graph:=p;
end;
Добавление дуги
Процедура добавления дуги AddArc в граф использует в качестве входной информации ссылки на соединяемые вершины и значения вес создаваемой дуги. Обе вершины должны существовать к моменту выполнения процедуры.
Procedure AddArc(u,v:refnode; y:integer);
Var a:refarc;
Begin if u=nil or v=nil then writeln(‘Отсутствует вершина’)
Else begin
New(a);
With a^ do begin
Infarc:=y;
Adj:=v;
Next:=u^.arclist
End;
u^.arclist:=a
end
end;
Создание графа
Вначале добавить все необходимые вершины графа процедурой AddNode, а затем добавить дуги процедурой AddArc.