Операции над бинарными деревьями: удаление вершины дерева.
При удалении вершины со значением поля inf=x из дерева надо рассмотреть три возможных варианта
1. Узла со значение, равным х , нет.
2. Узел со значением х имеет не более одного потомка.
Если вершина является конечной или из нее выходит только одно ребро, то нужно изменить соответствующую ссылку у предшествующей вершины:
Если удаляемый узел имеет только одного "сына", то его значение
можно заменить значением этого "сына"
3. Узел со значением х имеет двух потомков.
Если у удаляемого элемента 2 "сына", заменяем его элементом с
наименьшим значением среди потомков правого "сына" (или элементом с
наибольшим значением среди потомков левого "сына")
Процедура Delete выполняет все описанные действия, используя
вспомогательную процедуру del .
procedure Delete (var root:refnode; x:integer);
var q:refnode;
procedure del(var r:refnode);
begin
if r^.right<>nil then del(r^.right)
else begin
q^.inf:=r^.inf;
q:=r;
r:=r^.left;
end
end;
begin
if root=nil then write(“Такой вершины в дереве нет”)
else if x<root^.inf then Delete(root^.left,x)
else if x>root^.inf then Delete(root^.right,x)
else
begin {удаляем вершину, на которую указывает root}
q:=root;
if q^.right=nil then
root:=q^.left
else
if q^.left=nil then
root:=q^.right
else
del(q^.left);
dispose(q);
end;
end;
Понятие сбалансированности бинарного дерева. Приведение дерева к авл-сбалансированному виду: виды и формулы поворотов.
Идеальное дерево - дерево, в котором все вершины располагаются на h уровнях: корень - на 1-м, две вершины на 2-м, четыре - на 3-м. Новая вершина может быть помещена только на h+1 уровень. Количество операций при поиске и вставке в деревьях этого вида O(h) или O(log n) .
Вырожденное дерево - дерево, которое представляет собой линейный список элементов, упорядоченных по возрастанию или убыванию информационных полей, количество операций при поиске и вставке O(n) .
Бинарное дерево назовем идеально сбалансированным, если для каждой его
вершины количество вершин в левом и правом поддереве различаются не более
чем на 1
Бинарное дерево поиска называется сбалансированным по высоте, если для
каждой его вершины высота ее двух поддеревьев различается не более, чем на 1.
Деревья, удовлетворяющие этому условию, часто называют АВЛ-деревьями
Есть 4 варианта нарушения балансировки:
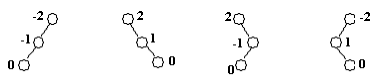
LL-поворот
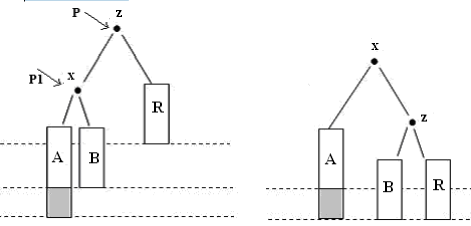
Надо преобразовать дерево t в новую форму: (A x B) z R ⇒ A x (B z R)
p1 := p^.left;
p^.left := p1^.right;
p1^.right := p;
p := p1;
RR-поворот
Симметричная ситуация имеет место, если новая вершина включается в
поддерево R дерева t=A x (b z R) . В этом случае преобразование балансировки
будет обратным: A x (B z R) ⇒ (A x B) z R
p1 := p^.right;
p^.right := p1^.left;
p1^.left := p;
p := p1;
LR-поворот
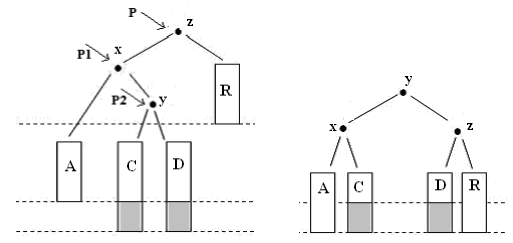
Преобразование (A x (C y D)) z R ⇒ (A x C) y (D z R)
Фрагмент программы:
p1 := p^.left;
p2 := p1^.right;
p1^.right := p2^.left;
p2^.left := p1;
p^.left := p2^.right;
p2^.right := p;
p := p2;
RL-поворот
Двукратный (двойной) R-L-поворот выполняется, когда «перевес» идет по
пути R-L от узла с нарушенной балансировкой. Выполняется преобразование:
A x ((C y D) z R) ⇒ (A x C) y (D z R) .
Фрагмент программы:
p1 := p^.right;
p2 := p1^.left;
p1^.left := p2^.right;
p2^.right := p1;
p^.right := p2^.left;
p2^.left := p;
p := p2;