Методы поиска: линейный поиск, метод бинарного поиска, поиск с помощью бинарного дерева, метод случайного поиска и др.
Линейный, последовательный поиск — алгоритм нахождения заданного значения произвольной функции на некотором отрезке. Данный алгоритм является простейшим алгоритмом поиска и в отличие, например, от двоичного поиска, не накладывает никаких ограничений на функцию и имеет простейшую реализацию. Поиск значения функции осуществляется простым сравнением очередного рассматриваемого значения (как правило поиск происходит слева направо, то есть от меньших значений аргумента к большим) и, если значения совпадают (с той или иной точностью), то поиск считается завершённым.
Бинарный поиск –
Если у нас есть массив, содержащий упорядоченную последовательность данных, то очень эффективен двоичный поиск.
Переменные Lb и Ub содержат, соответственно, левую и правую границы отрезка массива, где находится нужный нам элемент. Мы начинаем всегда с исследования среднего элемента отрезка. Если искомое значение меньше среднего элемента, мы переходим к поиску в верхней половине отрезка, где все элементы меньше только что проверенного. Другими словами, значением Ub становится (M – 1) и на следующей итерации мы работаем с половиной массива. Таким образом, в результате каждой проверки мы вдвое сужаем область поиска. Так, в нашем примере, после первой итерации область поиска – всего лишь три элемента, после второй остается всего лишь один элемент. Таким образом, если длина массива равна 6, нам достаточно трех итераций, чтобы найти нужное число.
Поиск с помощью бинарного дерева
Если дерево пусто, сообщить, что узел не найден, и остановиться.
Иначе сравнить K со значением ключа корневого узла X.
Если K=X, выдать ссылку на этот узел и остановиться.
Если K>X, рекурсивно искать ключ K в правом поддереве Т.
Если K<X, рекурсивно искать ключ K в левом поддереве Т.
Случайный поиск
Случайным образом задается индекс в массиве, сравнивается элемент массива имеющий этот индекс с исходным, если равен, то возвращается индекс, если нет то операция повторяется.
Метод крайне неэффективен.
Алгоритмы внешней сортировки: метод естественного слияния, метод сбалансированного слияния. Двухпутевая и многопутевая реализации. Фибоначчиева сортировка.
Внешняя сортировка - это сортировка последовательных файлов, располагающихся во внешней памяти, размер которых слишком велик, чтобы можно было целиком переместить их в основную память и применить один из методов внутренней сортировки. Наиболее часто внешняя сортировка применяется в системах управления базами данных при выполнении запросов, и от эффективности применяемых методов существенно зависит производительность СУБД.
Очевидно, что любой алгоритм сортировки файла требует изъятия каких-то элементов из файла и включения их в файл на новые места. Таким образом, часть файла должна быть переписана на новое место (в новый файл или несколько новых файлов), а затем эти новые файлы должны быть объединены (слиты). Основным понятием будем считать понятие отрезка файла. Отрезком длины k является последовательность записей A i , A i+1 ,…A i+k-1 такая, что в ней все записи упорядочены по заданному ключу key.
Естественное слияние
При использовании метода прямого слияния не принимается во внимание то, что исходный файл может быть частично отсортированным.
Первая серия упорядоченных записей и переписывается в файл B, вторая - в файл C и т.д. При слиянии первая серия записей файла B сливается с первой серией файла C, вторая серия B со второй серией C и т.д. Если просмотр одного файла заканчивается раньше, чем просмотр другого (по причине разного числа серий), то остаток файла целиком копируется в конец файла A. Процесс завершается, когда в файле A остается только одна серия
Сбалансированное многопутевое слияние.
В основе метода внешней сортировки сбалансированным многопутевым слиянием
является распределение серий исходного файла по m вспомогательным файлам B1, B2 , ..., Bm.. Затем производится их слияние первых серий каждого файла в файл C1, вторых серий – в файл C2 и т.д. На следующем шаге производится слияние файлов C 1 , C 2 , ..., C m в файлы B 1 , B 2 , ..., B m и т.д., пока в B 1 или C 1 не образуется одна серия.
Простой пример трёхпутевого слияния:
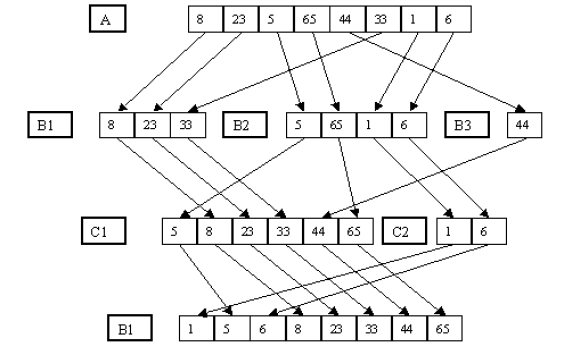
Многофазная сортировка
При использовании рассмотренного выше метода сбалансированной многопутевой внешней сортировки на каждом шаге примерно половина вспомогательных файлов используется для ввода данных и примерно столько же для вывода сливаемых серий. Идея многофазной сортировки состоит в том, что из имеющихся m вспомогательных файлов (m-1) файл служит для ввода сливаемых последовательностей, а один - для вывода образуемых серий. Как только один из файлов ввода становится пустым, его начинают использовать для вывода серий, получаемых при слиянии серий нового набора (m-1) файлов. Таким образом, имеется первый шаг, при котором серии исходного файла распределяются по m-1 вспомогательному файлу, а затем выполняется многопутевое слияние серий из (m-1) файла с записью в файл m, пока один из них не станет пустым. Метод трехфазной внешней сортировки дает желаемый результат и работает максимально эффективно (на каждом этапе сливается максимальное число серий), если начальное распределение серий между вспомогательными файлами описывается суммами соседних числел Фибоначчи.
Понятие хеширования. Построение хеш-функции. Разрешение коллизий, линейное рехеширование, случайное рехеширование, квадратичное рехеширование, метод цепочек (списковое и матричное представление).
Для сокращения времени доступа к данным в таблицах используется так называемое случайное упорядочивание или хеширование.
Хеш-таблица – это обычный массив с необычной адресацией, задаваемой хеш-функцией.
Хеширование (глагол «hash» в английском языке означает «рубить, крошить») применяется, когда реальное количество записей значительно меньше, чем количество возможных ключей.
Если входной поток информации абсолютно случаен, то в качестве хеш-функции можно использовать, например, функцию: h(a)=code(a) mod N
При заполнении таблицы возникают ситуации, когда для двух неодинаковых ключей функция вычисляет один и тот же адрес: ki ≠ kj ; h(ki) = h(kj) . Данный случай носит название коллизия, а такие ключи называются ключи-синонимы.
Разрешение коллизий достигается путём рехеширования – специального алгоритма, который используется при размещении новой записи или при поиске существующей.
h(a)=(B code(a) +C) mod N, где B и C – константы
При большом количестве элементов с одинаковым значением адреса будет получены кластеры (блоки) - последовательности подряд идущих записей, соответствующих одному и тому же адресу.
Методы разрешения коллизий:
Метод линейного рехеширования. Сводится к последовательному перебору элементов таблицы с некоторым фиксированным шагом c. a=(h(key) + c*i) mod N , где i номер попытки разрешить коллизию. При c=1 происходит последовательный перебор всех элементов после текущего.
Метод случайного рехеширования. Определяется формулой: а=(h(key)+r) mod N, где r – случайное число из некоторого фиксированного набора.
Этот подход не способствует образованию больших блоков, скорее, объекты равномерно рассеиваются по таблице.