2 Пересылки записей

случайное число пересылок

1 Пересылка записи

end

Математическое ожидание количества пересылок в цикле While при условии, что новый элемент вставляется в уже отсортированную последовательность длиной i равна i/2, т.е. в среднем придется просмотреть половину последовательности, до тех пор, пока не найдется подходящее место.

Получается, что в начале работы алгоритма сортировки вставками (начинаем с i=2) у нас имеется отсортированная последовательность из одного элемента, количество перестановок может быть либо 1 (1-й элемент меняем местами со 2‑м элементом), либо 0 (т.к. 2-й элемент уже находится на своем месте).

При i=3 (длина отсортированной последовательности равна двум) возможны три варианта: 0 пересылок, 1 пересылка, 2 пересылки. По определению математического ожидания количество пересылок равно 1.

Таким образом, при i=n (длина отсортированной последовательности равна n–1) количество пересылок может быть от 0 до n–1. Математическое ожидание количества пересылок при условии, что в среднем придется просмотреть половину последовательности из n–1 элемента, будет равно (n‑1)/2.

Тогда

M_ср=3(n-1)+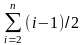 =3(n-1)+1/2(1+2+...+(n-1))=

=3(n-1)+1/2·n·(n-1)/2=3(n-1)+(n²-n)/4=

=3n-3+(n²-n)/4=(12n-12+n²-n)/4=

=(n²+11n-12)/4.

15. Методы сортировок: алгоритм быстрой сортировки. Анализ сложности алгоритма быстрой сортировки.

Алгоритм:

• выбрать элемент, называемый опорным.

• сравнить все остальные элементы с опорным, на основании сравнения разбить множество на три — «меньшие опорного», «равные» и «большие», расположить их в порядке меньшие-равные-большие.

• повторить рекурсивно для «меньших» и «больших».

procedure hoarsort( var mas: array[1..100] of integer; a,b:integer);//при начальном вызове a=1 b=количеству элементов массива

var i,j,m,k:integer;

begin

i:=a;

j:=b;

if (a>=b) then

else

begin

m:=mas[(a+b)div 2];

while i<=j do

begin

while mas[i]>m do

inc(i);

while mas[j]<m do

j:=j-1;

if i<=j then

begin

k:=mas[i];

mas[i]:=mas[j];

mas[j]:=k;

inc(i);

j:=j-1;

end;

end;

hoarsort(mas,a,j);

hoarsort(mas,i,b);

end;

end;

+ оценка сложности

16. Обзор методов сортировок: сортировка Шелла, пирамидальная сортировка, сортировка слияниями, Шейкер-сортировка, сортировка подсчетом, цифровая сортировка и др.

Сортировка Шелла:

Идея метода: делим массив на k1 групп, каждую группу сортируем, далее делим массив на k2 групп (k2<k1), снова сортируем полученные группы, далее на k3 групп (k3<k2<k1), и т.д. в конце делим на kn групп, причем kn = 1, т.е. в конце сортируем весь массив.

Значения k1, k2, k3, …, kn называются приращениями.

Лучшим считается выбор в качестве значений приращений взаимно простых чисел.

Сортировка фон Неймана (слиянием)

Метод основан на идее слияния двух отсортированных частей массива, поэтому первоначально массив разбивается на две части, которые независимо сортируются, а затем результаты сливаются в единое целое. С каждой из частей выполняются аналогичные действия, до тех пор, пока количество элементов в сортируемой части массива не станет равно двум. В этом случае выполняется простое сравнение элементов и их перестановка, если она необходима.

Пирамидальная сортировка:

1. Построение пирамиды Пирамида представляет собой дерево, в котором каждый узел имеет не более двух потомков, причем узел всегда больше или равен своим потомкам (таким образом, на вершине дерева всегда находится наибольший элемент). Если в исходном массиве n элементов, то последние (n / 2) элемента становятся основанием пирамиды (эти элементы являются листьями дерева, т.е. у них нет потомков, поэтому для них вышеуказанное правило выполняется автоматически). Удобнее всего поместить пирамиду в массив. При этом распределение индексов массива по узлам дерева будет выглядеть так (на этом рисунке все цифры - это индексы элементов массива, а ни в коем случае не значения этих элементов): Таким образом, для того, чтобы каждый узел дерева был больше своих потомков, каждый элемент массива a[i] должен быть больше или равен элементам a[2 * i + 1] и a[2 * i + 2]. 2. Сортировка. В этой части алгоритма мы перемещаем в конец массива максимальный элемент, затем исключаем его из дальнейшего процесса сортировки. Поскольку максимальный элемент всегда находится на вершине пирамиды, мы должны поменять местами элементы a[0] и a[n-1] (т.е. последний элемент). Причем элемент a[n-1] необходимо добавлять так, чтобы не нарушился порядок пирамиды (при этом пирамиду придется частично перестроить). Далее мы будем рассматривать массив только до (n-2)-го элемента. На следующем шаге мы меняем местами a[0] и a[n-2] и далее рассматриваем массив только до (n-3)-го элемента. Повторяем всю эту процедуру до тех пор, пока в рассматриваемой части массива не останется один элемент.

Шейкер сортировка:

Это модификация метода «пузырька», которая учитывает два дополнительных требования:

1) устранение «лишних» просмотров массива, т.е. если массив уже отсортирован за первые проходы, последующие проходы не делаем. Пример: 12,3,5,7,9,10.

2) смена направлений прохода массива: сначала проходим от начала к концу, по том – от конца к началу, потом снова от начала к концу и т.д. Это позволяет уменьшить число проходов по массиву. Пример: 5,7,9,10,12,3.

Сортировка подсчетом:

Идея алгоритма состоит в том, чтобы для каждого элемента x предварительно подсчитать, сколько элементов входной последовательности меньше x. После этого х записывается напрямую в выходной массив в соответствии с этим числом. Например, если семнадцать элементов входного массива меньше х, то в выходном массиве х должен быть записан на место с номером восемнадцать.  Используются следующие обозначения:  A[1..n] - входная последовательность;  C[1..k] - вспомогательный массив из k элементов;  B[1..n] - выходная отсортированная последовательность.  Работа алгоритма заключается в следующем.  В элемент C[i] заносится количество элементов массива A, равных i.  Затем находятся частичные суммы последовательности C[1], C[2], ..., C[k], каждая из которых является количеством элементов, не превосходящих i.  После этого каждый элемент A[i] из входного массива помещается в выходной массив B на позицию, равную значению элемента С[A[i]].

Цифровая сортировка:

Этой сортировкой можно сортировать целые неотрицательные числа большого диапазона. Идея состоит в следующем: отсортировать числа по младшему разряду, потом устойчивой сортировкой сортируем по второму, третьему, и так до старшего разряда.