Оптимизация алгоритмов. Примеры.
Поиск алгоритма min сложности – оптимизация алгоритма.
Одна из задач, которая обычно ставится при разработке алгоритмов и программ - минимизация требуемых программой ресурсов. Особенно это касается системного программного обеспечения: программ операционной системы, трансляторов, систем управления базами данных и знаний и т. д., т.е. программ, имеющих большое количество пользователей и испытывающих как товар, большую конкуренцию на рынке программных средств.
Существует несколько самостоятельных аспектов оптимизации программ, из которых выделим два:
оптимизация, связанная с выбором метода построения алгоритма;
оптимизация, связанная с выбором методов представления данных в программе.
Первый вид оптимизации имеет глобальный характер и (при удачной оптимизации) ведет к уменьшению порядка функции сложности - например, замена алгоритма с Т(V) = O(VS) на алгоритм с T(V) = O(V4). Он зависит от того, как задача разбивается на подзадачи, насколько это разбиение свойственно самой задаче или является только искусственным приемом.
Второй вид оптимизации, не меняя структуры программы в целом, ведет к экономии памяти и/или упрощению работы со структурами данных, повышению эффективности вспомогательных процедур, обеспечивающих "интерфейс" между прикладным уровнем (на котором мыслим в терминах высокоуровневых объектов - графов, матриц, текстов и т. д.) и машинным уровнем, поддерживающим простейшие типы данных (числа, символы, указатели). Результатом этого обычно является уменьшение коэффициентов при некоторых слагаемых в функции сложности (при удачной оптимизации - при наиболее значимом слагаемом), но порядок функции сложности остается тем же.
Пример: вычисления числа Фибоначчи через формулу:
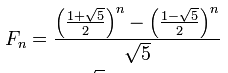
Понятие сложности задачи и классы сложности задач. Понятие сводимости, полиномиальная сводимость.
Задачи:
массовые (список параметров и формулировка условий)
частные (формальные параметры заменяются фактическими)
Сложность задачи – сложность самого простого алгоритма. Поиск алгоритма min сложности – оптимизация алгоритма.
Детерминированные вычисления – обычный, классический способ.
Недетерминированные вычисления – существует в нескольких параллельно работающих экземплярах. Недетерминированный вычислитель исполняет недетерминированные алгоритмы. Разрешаем шаги с неоднозначным результатом – шаги, вырабатывающие сразу несколько значений для одной переменной. Эти значения могут использоваться:
параллельно выполняющиеся процессы.
угадать, какое из значений, полученных на данном шаге, является правильным, и использовать только его.
Классы сложности задач:
полиномиальные - их временная сложность ограничивается сверху некоторым полиномом.
экспоненциальные – в общем случае требуется кол-во операций, увеличивающееся с ростом n по крайней мере экспоненциально.
NP – задачи, которые можно решить за полиномиальное время на недетерминированном вычислителе
Задача Q сводится к задаче Р за полиномиальное время, если существует детерминированный полиномиальный алгоритм, преобразовывающий произвольный частный случай задачи Р так, что ответом для данного случая задачи Q является «да» тогда и только тогда, когда ответом на соответствующий случай задачи Р также является «да».
вход для Q Вход для Р ответ Р Ответ Q
Полиномиальная сводимость – детерминированный полиномиальный алгоритм сводит одну задачу к другой
NPC – подкласс NP, любая задача NP сводится к ним