6.54 Коэффициент прозрачности для прямоугольного барьера______________________

Коэффициент прозрачности (вероятность проникновения

сквозь потенциальный барьер конечной ширины) ___________________________

D быстро убывает с увеличением ширины барьера, а также с ростом его высоты.

[U₀ — высота потенциального барьера; Е — энергия частицы; — ширина прямо­угольного барьера; т — масса частицы; — постоянная Планка; D₀ — по­стоянный множитель, который, как показывают точные расчеты, не очень отли­чается от единицы]

6.55 Коэффициент прозрачности для барьера произвольной формы ___________

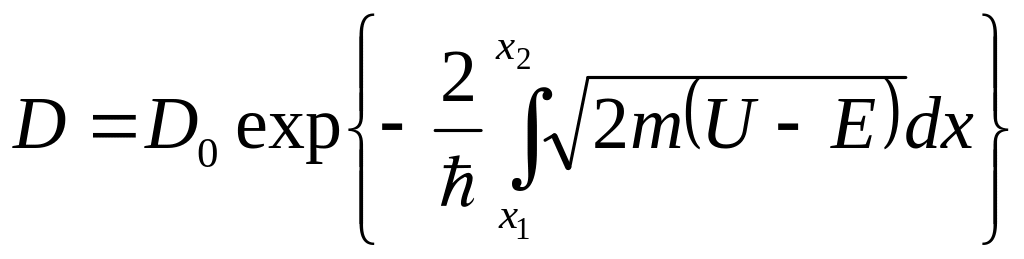
Эта формула — хорошее приближение в случае потенциального барьера произволь­ной формы, если барьер удовлетворяет ус­ловию квазиклассического приближения (достаточно гладкая форма кривой).

♦ Эта формула — обобщение формулы для D в случае прямоугольного барьера.

6.56 Выводы относительно поведения классической

и квантовой частиц_______________________________________________________

При Е < U₀ по классической теории частицы не смогут преодолеть потен­циального барьера и отразятся от него; согласно квантовой теории, часть частиц отражается, а часть имеет отличную от нуля вероятность пройти сквозь потенциальный барьер. При Е > U₀, по классической теории все частицы преодолевают потенциальный барьер; согласно квантовой тео­рии, часть частиц проходит, а часть отражается. Как подбаръерное про­хождение, так и надбарьерное отражение являются специфическими квантовыми эффектами, связанными с волновыми свойствами частиц.

6.2.11. Линейный гармонический осциллятор

Линейный (одномерный) гармонический осциллятор______________________________

Система, совершающая одномерное движение под действием квазиупругой силы. Задача о гармоническом осцилляторе в квантовой теории играет фундаментальную роль по двум причинам: 1) она встречается во всех задачах, где имеют место квантованные колебания (например, в квантовой теории поля, в теории молекулярных и кристаллических колебаний и т. д.); 2) проблемы, относящиеся к гармоническому осциллятору, — хорошая иллюстрация основных принципов и форм квантовой механики.

6.57 Описание гармонического осциллятора в квантовой механике_________________

Потенциальная энергия линейного гармонического осциллятора___________________

П отенциальная яма в данном случае является параболической.

Оператор Гамильтона для осциллятора__________________________________________

6 .37

Стационарное уравнение Шредингера в операторной форме________________________

Э то уравнение по внешнему виду совпадает с записанным выше уравнением 6.38, однако здесь другой оператор.

Уравнение Шредингера для гармонического осциллятора__________________________

Э то же уравнение получается при подстановке U в стационарное уравнение Шредингера 6.25.

[т — масса частицы; ω₀ — собственная частота колебаний осциллятора x - отклонение из положения равновесия; — оператор кинетической энергии; — оператор потенциальной энергии; - постоянная Планка; Е — полная энергия осциллятора; Ψ — координатная часть волновой функции]