
- •Розробка плану статистичного спостереження
- •1.2.Збір статистичної інформації
- •2.1. Статистичні зведення
- •3.1 Середні величини та показники варіації
- •3.2 Визначення відносних величин
- •3.3 Структурні середні
- •3.4 Характеристика рядів розподілу
- •3.5.Перенесення результатів вибіркового спостереження на генеральну сукупність.
- •3.6 Визначення показників та середніх показників рядів динаміки
- •3.6.1 Визначення трендових рівнянь
- •3.7.Аналіз взаємозв’язку між факторною та результативною ознакою.
3.1 Середні величини та показники варіації
При вивчені масових явищ одна з основних задач статистики є визначення окремих властивостей кожної сукупності явища. Для того щоб виявити характерні особливості сукупності, використовують середні величини. Основними серед них є:середня арифметична, середня гармонічна, середня квадратична і середня геометрична.
Середня арифметична – основний вид середніх величин. Буває проста і зважена. Проста це сума індивідуальних значень варіюючої ознаки, що поділена на кількість одиниць сукупності. Зважена – середня із варіантів, що повторюється не однакову кількість раз чи має різну статистичну вагу.
Використовуємо середню арифметичну зважену, оскільки сукупність згрупована, а частоти варіантів задані явно:
Ẍ=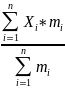
Де
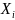 - індивідуальні
значення ознаки
- індивідуальні
значення ознаки
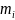 -
абсолютна
кількість повторення варіюючої
ознаки(частота).
-
абсолютна
кількість повторення варіюючої
ознаки(частота).
Визначимо середню суму виробітку:
Ẍ=((1+1,5)/2*8+(1,5+2)/2*7+(2+2,5)/2*0+(2,5+3)/2*7+(3+3,5)/2*0+(3,5+4)/2*8)/30=2,38 – середній тип кузова
Середня вантажопід`ємность
Ẍ=((3,5+3,83)/2*8+(3,83+4,17)/2*8+(4,17+4,5)/2*5+(4,5+4,83)/2*0+(4,83+5,17)/2*5+(5,17+5,5)/2*4)/30= 4,31
Середня Q вантажу
Ẍ((295+311,67)/2*2+(311,67+328,33)/2*1+(328,33+345)/2*12+(345+361,67)/2*6+(361,67+378,33)/2*5+(378,33+395)/2*4)/30= 349,44
Показники варіації:
а) розмах варіації
Rx=Xmax-Xmin
б)Середнє лінійне відхилення
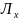 =
=
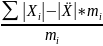
в)Середнє
квадратичне відхилення
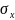 показує на скільки в середньому
індивідуальне значення відхиляється
в середньому від середнього, з урахуванням
знаку відхилення.
показує на скільки в середньому
індивідуальне значення відхиляється
в середньому від середнього, з урахуванням
знаку відхилення.
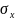 =
=
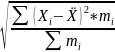
г)дисперсія
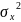 =
=
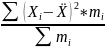
д)коефіцієнт варіації
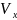 =
=
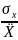 *100%
*100%
Проведемо розрахунок показників варіації для ознак: сума виробітку,кількість робочих днів,кількість працюючих – за даними таблиць 2.6 – 2.9
Визначаємо показники варіації для ознаки тип кузова
А) Rx=4-1= 3
Тип кузова змінюється в межах 3
Б)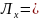 |(((1+1,5)/2)-2,38)|*8+|(((1,5+2)/2)-2,38)|*7+|(((2+2,5)/2)-2,38)|*0+|(((2,5+3)/2)-2,38)|*7+|(((3+3,5)/2)-2,38)|*0+|(((3,5+4)/2)-2,38)|*8)/30=
0,9
|(((1+1,5)/2)-2,38)|*8+|(((1,5+2)/2)-2,38)|*7+|(((2+2,5)/2)-2,38)|*0+|(((2,5+3)/2)-2,38)|*7+|(((3+3,5)/2)-2,38)|*0+|(((3,5+4)/2)-2,38)|*8)/30=
0,9
В середньому індивідуальні значення типу кузова відхиляються на 0,9
В)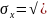 =
0,95
=
0,95
Середнє квадратичне відхилення індивідуальних значень типу кузова становить 0,95
Ступінь варіації об’єктивніше відображає показник середнього квадрата відхилення (дисперсія). Його обчислюють як середню арифметичну з суми квадратів відхилень окремих варіантів від їхньої середньої :
Г)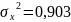
Д)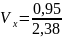 *100%=39,87%
*100%=39,87%
Дана сукупність по ознаці сума виробітку не однорідна ,а ознаки змінюються не суттєво.
Визначаємо показники варіації для ознаки кількість працюючих:
А) Rx=5,5-3,5=2 (тони)
Вантажопід`ємность змінюється в діапазоні 2 (тон)
Б)
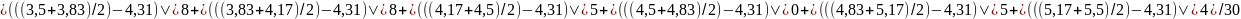 =0,51
=0,51
В середньому індивідуальні значення Вантажопід`ємності відрізняються на 0,51 (тон)
В)
=
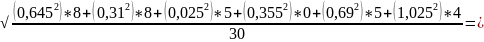 0,6
0,6
Середнє квадратичне відхилення індивідуальних значень Вантажопід`ємност становить 0,6 (тон)
Г)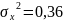
Д)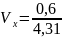 *100%=13,84%
*100%=13,84%
Дана сукупність по ознаці Вантажопід`ємность – однорідна.
Визначаємо показники варіації для ознаки Q вантажу:
А) Rx=395-295=100 (тон/день)
Q вантажу змінюється в межах 100 тон/день.
Б)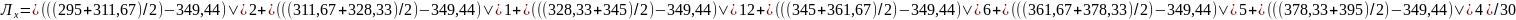 =18,33
=18,33
В середньому індивідуальні значення Q вантажу відрізняються на 18,33 (тон/днів)
В)
=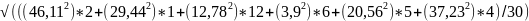 =22,32
=22,32
Середнє квадратичне відхилення індивідуальних значень за ознакою Q вантажу становить 22,32 тон/днів
Г)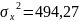
Д)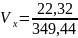 *100%=6,36%
*100%=6,36%
Дана сукупність по ознаці Q вантажу – не однорідна.
