Тема 5. Ряды динамики: – выявление и характеристика основной тенденции развития, скользящая средняя, аналитическое выравнивание, интерполяция, экстраполяция.

Социально-экономические явления общественной жизни находятся в непрерывном развитии. Их изменение во времени статистика изучает при помощи построения и анализа рядов динамики. Ряд динамики – числовые значения статистического показателя, представленные во временной последовательности. Он состоит из двух граф: в первой – указываются периоды (или даты, во второй – показатели, характеризующие изучаемый объект за эти периоды (или на эти даты).

Показатели второй графы носят название уровней ряда: первый показатель называется начальным уровнем, последний – конечным, уровень любого периода (кроме первого) называется уровнем текущего периода.

Выявление общей тенденции изменения динамического ряда обеспечивается при помощи особых приемов. Наиболее простым способом является укрупнение интервалов и определение итога уровня для этих интервалов или исчисление средних для каждого укрупненного интервала, при этом используют либо переменную среднюю, либо скользящую среднюю.

Переменная средняя исчисляется по формуле простой средней арифметической.

Например, если укрупненный интервал образован объединением двух периодов. То средние для укрупненных интервалов определяются следующим образом: , , и т.д.

Скользящая средняя – подвижная динамическая средняя, которая исчисляется по ряду при последовательном передвижении на один интервал, т.е. сначала исчисляют средний уровень из определяемого числа первых по порядку уровней ряда, затем – средний уровень из такого же числа членов, начиная со второго. если в ряду динамики имеются периодические колебания, то период скользящей средней должен совпадать с периодом колебания или быть кратным ему. Если в ряду периодических колебаний нет, то период скользящей средней подбирают начиная с наименьшего, т.е. с двух уровней, если в этом случае тенденция не проявляется, то период укрупняют. Период скользящей может быть четным или нечетным, практически удобнее использовать нечетный период, т.к. в этом случае скользящая средняя будет оттеснена к середине периода скольжения.

Скользящие средние с продолжительностью периода, равной 3 следующие:

; ; ; и т.д.

Полученные средние записываются к соответствующему интервалу (второму, третьему и.д.). Сглаженный ряд "укорачивается" по сравнению с фактическим на члена с одного и другого конца, где – количество уровней, входящих в интервал.

Обеспечиваемое при применении способа скользящей средней погашение колебаний величин индивидуальных уровней ряда динамики называется сглаживанием динамического ряда.

Рассмотренные приемы выявления общей тенденции изменения динамического ряда не позволяют получить описание плавной линии развития (тренда) данного ряда. для этой цели используется аналитическое выравнивание, сущность которого заключается в нахождении уравнения, выражающего закономерность изменения явления как функцию времени . Вид уравнения определяется характером динамики развития конкретного явления; если первые разноси уровней приблизительно равны, сглаживание может быть выполнено по прямой. выбор формы кривой может быть основан на анализе графического изображения уровней динамического ряда, (линейной диаграммы), при этом целесообразнее воспользоваться графическим изображением сглаженных уровней, в которых случайные колебания погашены. Наиболее часто используются виды трендовых моделей: линейная – , парабола второго порядка – .

Коэффициенты и для линейной модели находятся из системы нормальных уравнений

Вычислительный процесс нахождения параметров уравнения при сохранении полной идентичности конечных результатов может быть значительно упрощен, если ввести обозначения дат (периодов) времени с помощью натуральных чисел , с тем, чтобы .

а) если количество уровней в ряду динамики нечетное, то временные даты обозначаются следующим образом

Временные даты (периоды)	январь	февраль	март	апрель	май
Уровни ряда динамики
Обозначения временных дат	-2	-1	0	1	2

б) если количество уровней в ряду динамики четное, то обозначения временных дат будут следующие

Временные даты (периоды)	январь	февраль	март	апрель	май	июнь
Уровни ряда динамики
Обозначения временных дат	-5	-3	-1	1	3	5

Тогда система нормальных уравнений при выравнивании по прямой примет вид: , откуда , .

Для упорядочения расчета сумм целесообразно ввести таблицу, например, при выравнивании по прямой

Дата	Уровни ряда динамики	Обозначения временных дат
	…

По полученной модели для каждого периода (каждой даты) определяются теоретические уровни тренда ( ) и стандартная ошибка аппроксимации (среднее квадратическое отклонение) по формуле

;

, – расчетные и фактические значения уровней,

– число уровней ряда,

– число параметров в уравнении тренда.

Аналитическое сглаживание позволяет не только определить общую тенденцию изменения явления на рассматриваемом отрезке времени, но и выполнять расчеты для таких периодов, в отношении которых нет исходных данных.

Нахождение по имеющимся данным за определений период времени некоторых недостающих значений признака внутри этого периода называется интерполяцией.

Нахождение значений признака за пределами анализируемого периода называется экстраполяцией. Применение экстраполяции для прогнозирования должно основываться на предположении, что найденная закономерность развития внутри динамического ряда сохраняется и вне этого ряда.

Задача 5.

Динамика роста числа гражданских исков, принятых к рассмотрению в районных судах, по городу представлена в таблице.

Требуется:

1) произвести сглаживание ряда методом трехлетней скользящей средней;

2) выровнять ряд по прямой;

3) методом экстраполяции определить прогноз показателя на 2002 г

4) начертить графики первичного и вторичного рядов.

	1994	1995	1996	1997	1998	1999	2000	2001
	360	381	401	422	443	463	485	505

Составим вспомогательную таблицу

Дата	Уровни ряда динамики		первые разности				Теоретический уровень
1	2	3	4	5	6	7	8	9
1994	360	–	–	-7	49	-2520	359,7	0,09
1995	381	380,7	21	-5	25	-1905	380,5	0,25
1996	401	401,3	20	-3	9	-1203	401,3	0,09
1997	422	422,0	21	-1	1	-422	422,1	0,01
1998	443	442,6	21	+1	1	443	442,9	0,01
1999	463	464,0	20	+3	9	1389	463,7	0,49
2000	485	484,0	22	+5	25	2425	484,5	0,25
2001	505	–	20	+7	49	3535	505,3	0,09
Итого	= 3460			0	168	1742	3460	1,28

Для нахождения и используется система нормальных уравнений

;

Для упрощения системы уравнений показатели времени ,обозначаются так, чтобы , тогда система принимает вид: .

Откуда , ..

Модель тренда (линия развития после аналитического выравнивания): .

Вычислим теоретические уровни (графа 8).

Например: и т.д.

Точечный прогноз на 2002г.

(число гражданских исков)

1998г.

2000г.

Графики первичного, выровненного ряда и объем

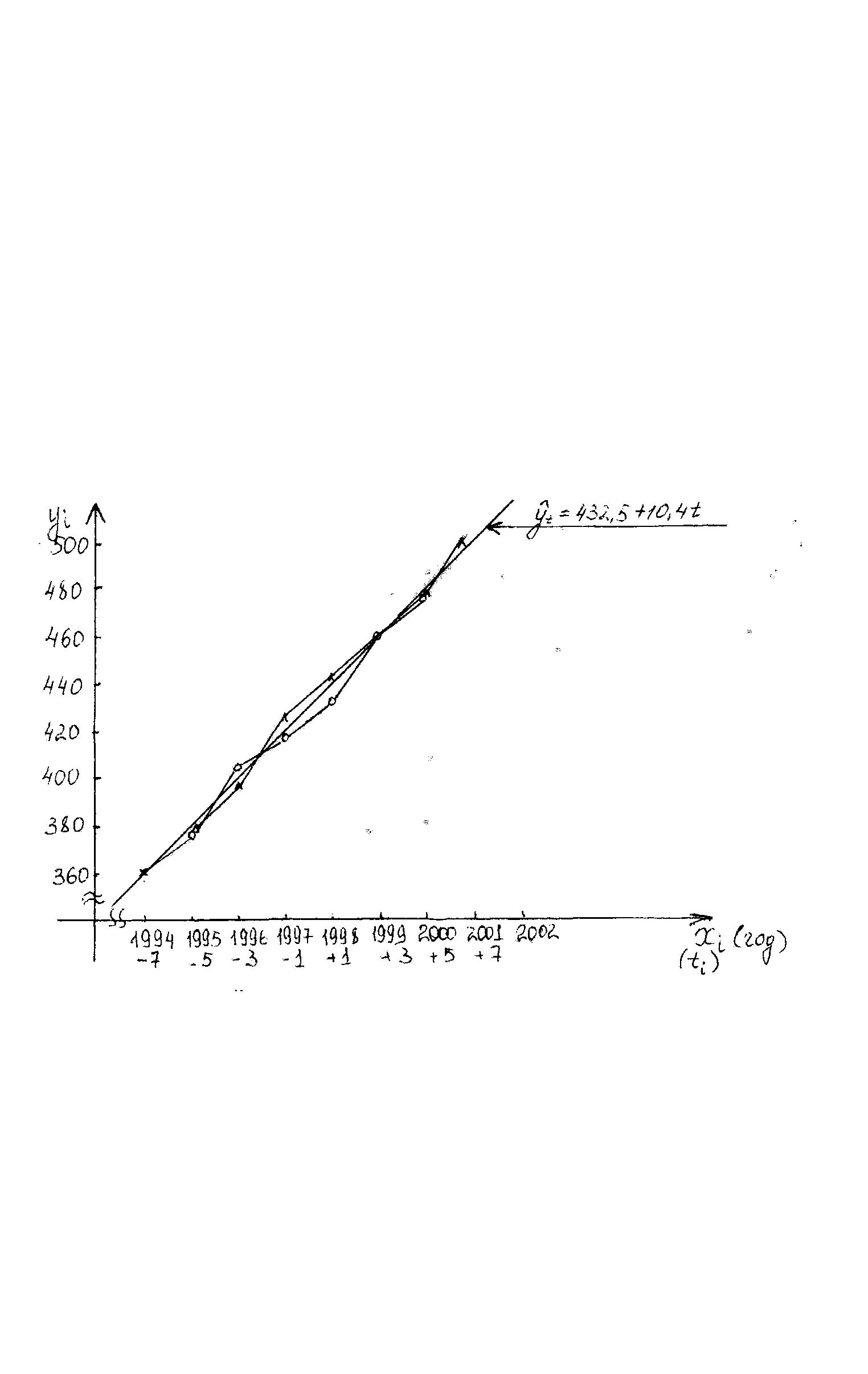
– первичный ряд

– выровненный ряд

– теоретическая кривая

1998г.

2000г.