Матриця класифікації пп

	Класифіковано ПП
Фактично	Ненадійний	Сумлінний	Усього
Ненадійний	57	18	75
Сумлінний	26	49	75
Усього	63	87	150

Результатна оцінка класифікації, а отже, продуктивності класифікаційної моделі, випливає із поверхневого погляду на матрицю. Із 75-ти платників податків, що належать до класу Ненадійний, такими були підтверджені моделлю тільки 57. 18-ть недисциплінованих ПП модель помилково віднесла до сумлінних. Аналогічно із 75-ти ПП, що належать до класу Сумлінний, 49 підприємств були віднесені моделлю до цього класу і 26 сумлінних платників модель помилково відзначила, як Ненадійних. Можна оцінити цей класифікатор таким, що скоріше помиляється при класифікації сумлінних ПП, тобто модель схильна до пропуску правильних рішень.

Таким чином, загальна помилка класифікації дорівнює: (18 + 26) / 150 ^х 100% = 29,3%.

На основі такої оцінки аналітик може зробити такі висновки про якість класифікаційної моделі:

• вищенаведена матриця класифікації показує, яка питома вага від загального числа прикладів розпізнана неправильно. Залежно від особливостей розв’язуваного завдання і необхідної точності допускається певний відсоток неправильно розпізнаних ПП. Наприклад, якщо виявилося, що число неправильно розпізнаних прикладів не перевищує 10%, то модель можна вважати працездатною. В іншому випадку необхідно відкоригувати параметри моделі для її покращення;

• результатна матриця класифікації дозволяє визначити класи, для яких допущено найбільше число помилок розпізнавання.

В даному випадку можна визнати, що головною перевагою наведеного візуалізатора є наочне і оперативне представлення результатів роботи моделі. У випадку отримання оціночної інформації зі звичайної таблиці, де представлена результативна вибірка, то при великій кількості об’єктів цей процес займає багато часу, зусиль та можлива також й помилкова інформація.

Застосування діаграми розсіювання. Наступним найважливішим завданням дейтамайнінгу (поряд із класифікацією) — є регресія. Основна відмінність регресії від класифікації полягає у тому, що вихідна змінна є безперервною (детальніше класи завдань дейтамайнінгу розглядаються в розділах 2 і 3), тому використання матриць класифікації для оцінки якості регресійних моделей є неприйнятним. Регресія просто встановлює взаємний зв’язок між значеннями вхідних і вихідних змінних моделі, яка оцінюється.

Основним методом візуалізації, який застосовується для оцінки якості моделей у випадку безперервної вихідної змінної, є діаграма розсіювання. Діаграма розсіювання — це графік, по одній осі якого відкладаються цільові значення вихідної змінної (тобто ті, які задані як еталон для навчання), а по іншій осі — реальні значення, отримані на виході моделі. На такому графіку можна побудувати лінію ідеальних значень: z = z’. На цій лінії лежатиме будь-яка точка, для якої реальне вихідне значення y, що сформовано моделлю, дорівнюватиме цільовому значенню z’ (при цьому помилка P = z — z’ = 0). Така лінія, очевидно, буде виходити із початку координат і перетинати координатну площину діагонально зліва направо. (замінити ’ на ' і далі по тексту, де позначено жовтим)

При відображенні цих даних на графіку будь-яка точка, для якої реальне вихідне значення є відмінним від еталонного цільового значення, відхилиться від лінії ідеальних значень. При цьому величина відхилення дорівнюватиме помилці, допущеній моделлю на даному прикладі (рис. 15).

Рис. 15. Побудова діаграми розсіювання

Теоретично представлена точка, що лежить на лінії ідеальних значень (діагональ), відповідає випадку, коли реальний вихід моделі дорівнює еталонному. На практиці модель допускає помилку Р, яка призводить до відхилення точки, що відповідає реальному виходу моделі, від еталонного, а отже, від лінії ідеальних значень. Точка, що відповідає реальному виходу, має координати z’ = z + P з врахуванням помилки.

Якщо уявити множину точок на площині (z z’), що утворені парами цільових і реальних значень, цей результат буде представлено на діаграмі у вигляді «хмари», що розсіяна вздовж лінії ідеальних значень. Ступінь відхилення точки від цієї лінії визначатиметься помилкою моделі на відповідному прикладі. Приклад діаграми розсіювання представлено на рис. 16. Діагональна лінія на рисунку — це лінія ідеальних значень. Точками, розсіяними вздовж лінії ідеальних значень, позначені реальні вихідні значення цільової моделі.

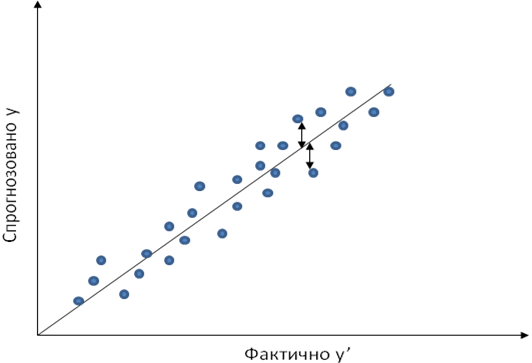
Рис. 16. Приклад діаграми розсіювання з незначними відхиленнями точок від діагоналі

І формально і змістовно інтерпретація діаграми розсіювання є досить прозорою. Якщо всі точки (або хоча б основна маса), що представляють реальні вихідні значення моделі, зосереджені поблизу лінії ідеальних значень, то можна вважати, що модель працює добре. Якщо у «хмари», що утворена точками виходів моделі, присутні значні розходження, то більшість вихідних значень має велику помилку і в цьому випадку якість моделі є незадовільною. Приклад такої діаграми розсіювання представлено на рис. 17, де переважна більшість точок значно віддалені від діагоналі.

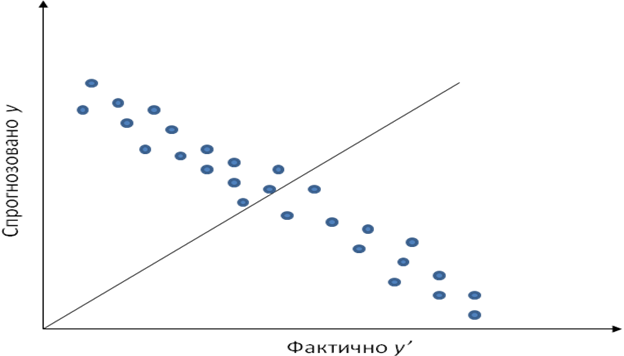
Рис. 17. Представлення діаграми розсіювання із суттєвими помилками моделі

У процесі оцінки аналітичних характеристик моделі особливий інтерес можуть представляти окремі точки, які найбільш віддалені від лінії ідеальних значень. Їх поява зумовлена тим, що на відповідних прикладах модель дає дуже високу помилку, оскільки в них містяться аномальні значення, що є нехарактерними для поведінки вибірки у цілому. Аналіз таких відхилень дозволяє виявляти рідкісні, але важливі події, що впливають на досліджуваний процес. Якщо ж аномальне значення — це просто наслідок помилки, то його слід виключити з розгляду або відкоригувати через змінення параметрів моделі.

Аналітикам для узагальненої оцінки точності моделі достатньо поверхневого погляду на діаграму розсіювання. За своєю суттю, вона є аналогом матриці класифікації для моделей з безперервними вихідними значеннями, що розглядались раніше.

Метод ретро-прогнозу. Досить поширений в аналітиці випадок завдань регресії — це прогнозування часових рядів. Для складання прогнозу будується регресійна модель, яка на основі минулих значень ряду розраховує прогнозовані значення. Ця модель має певний набір параметрів, що дозволяють отримати прогноз з урахуванням поведінки ряду в минулому (рис. 18) і можливостями налагодження потрібного результату.

Рис. 18. Типова діаграма прогнозу на основі часових рядів

Після проведення прогнозних розрахунків виникає досить важливе питання: наскільки коректно побудована модель прогнозу, наскільки вона точно і адекватно відповідає поведінці досліджуваного ряду? Для перевірки якості прогностичної моделі використовується спеціальний тип візуалізатора — так званий ретро-прогноз. Слово «ретро-прогноз» буквально означає «прогноз в минулому» або «прогноз минулих значень». Його сутність полягає в тому, щоб застосувати побудовану модель до підмножини даних з минулого і оцінити, наскільки отриманий прогноз відповідає реальним значенням ряду, що вже мали місце в минулому для певних проміжків часу.

На попередніх підготовчих стадіях ретро-прогнозу потрібно обрати певну підмножину даних з минулого для наступного використання їх як вихідних. Після цього до цієї підмножини застосовується прогностична модель із заданими параметрами. Модель формує набір прогнозних значень, які потім порівнюються з даними, які реально мали місце в минулому. Якщо в результаті такого порівняння виявиться, що між значеннями ретро-прогнозу і реальними даними існує велика розбіжність, це дозволяє поставити під сумнів коректність прогностичної моделі. Сам характер розбіжності (її величина, знак тощо) дає можливість сформулювати методику корекції моделі на наступних стадіях прогнозування.

Основний принцип роботи ретро-прогнозу пояснюється за допомогою діаграми на рис. 19, де розраховані значення ретро-прогнозу, позначені кубічними точками.

У процесі розрахунків значень моделі ретро-прогноз спрямований не у майбутнє ряду, а формується паралельно з його минулими значеннями і порівнюється з ними. На рис. 19 можна спостерігати достатньо добре узгодження значень ретро-прогнозу і реальних значень ряду, що дозволяє зробити припущення про високу якість прогностичної моделі, за допомогою якої був побудований ретро-прогноз. На рис. 20 представлено протилежний випадок, коли результатні дані ретро-прогнозу виявляються істотно завищеними або заниженими, що підтверджує недостатню точність моделі і необхідність подальшого її корегування.

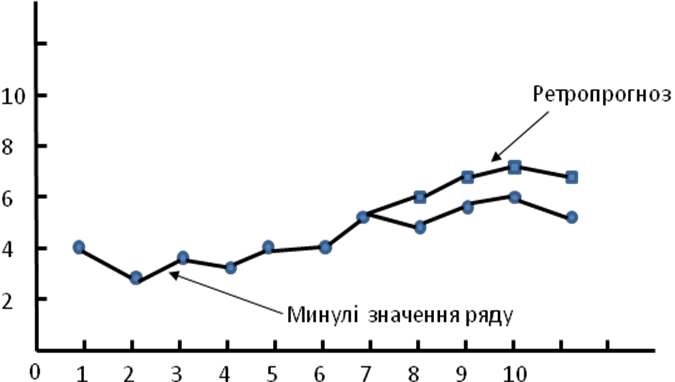
Рис. 19. Принцип дії ретропрогнозу.

Характерною особливістю вибору множини значень часового ряду (вихідних даних для ретро-прогнозу) є необхідність враховування його актуальності. У часовому ряді можна виділити два види даних — актуальні і застарілі. Перші сформовані під дією поточних умов, що впливають на процес, який описується часовим рядом. Умови можуть змінюватися, і тоді дані, які сформовано під дією умов, що втратили актуальність, виявляються застарілими, а дані, сформовані під дією нових умов, — актуальними. Зазвичай актуальними є найсвіжіші дані, що розташовані найближче до прогнозних періодів.

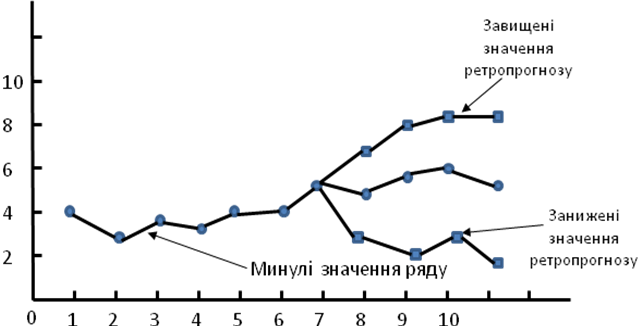
Рис. 20. Представлення ретро-прогнозу з великим відхиленням прогнозованих значень від реальних

У випадку застосування для розрахунку моделі прогнозу на основі актуальних даних ретро-прогноз повинен будуватися також на основі свіжих даних. Якщо ж ретро-прогноз базується на основі застарілих даних, то, ймовірніше, його значення досить сильно відрізнятимуться від реальності. При чому це буде пов’язано не з низькою якістю моделі, а з тим, що вона використовує застарілі дані, що залежать від інших закономірностей, яких в новій моделі немає. З урахуванням викладених обставин до інтерпретації результатів ретро-прогнозу слід підходити з певною обережністю щодо оцінки актуальності прогнозних даних.

Методи візуалізації контролю навчання моделей. В аналітичних технологіях широко використовуються моделі, засновані на машинному навчанні, наприклад нейронні мережі, дерева рішень тощо. У процесі налагодження своїх параметрів (або навчання) модель набуває властивостей, що забезпечують виконання нею необхідного перетворення даних згідно з обмеженнями.

Основним управлінським параметром, на основі якого розраховується зміна стану моделі на кожній ітерації, є помилка неузгодженості між реальним вихідним значенням моделі, яка була визначена на даному навчальному прикладі, і цільовим значенням з цього прикладу (тобто порівняння реальних і цільових значень).

Отримана в результаті обчислення помилка між реальним і цільовим виходом, що є результатом навчального процесу, — це головний критерій оцінки якості навчання і точності моделі. Очевидно, що в міру того, як модель навчається, помилка зменшується, і як тільки вона сягає певного заданого значення, процес навчання зупиняється внаслідок несуттєвості подальших можливих покращень.

Важливою характеристикою процесу навчання моделі є зміна вихідної помилки на кожній ітерації. Оцінка характеру змін помилки дозволяє дійти висновку про якість процесу навчання, про доцільність його продовження і передбачити його результати. Наприклад, якщо помилка швидко зменшується, це означає, що навчання просувається швидко і ефективно. Якщо помилка перестала зменшуватися і залишається однаковою, навіть для великої кількості ітерацій, можна припустити, що процес навчання «пробуксовує», тобто або стан моделі не коригується, або коригування не призводить до зменшення помилки. У цьому випадку навряд чи має сенс продовжувати навчання, оскільки модель вичерпала свої можливості і налаштувати її скоріш за все неможливо. Тому до складу аналітичних програм досить часто включають спеціальний візуалізатор, який дає можливість спостерігати за динамікою зміни помилок. Одну із можливих реалізацій такого візуалізатора наведено на рис. 21 у вигляді графічного уявлення значень зміни навчальних помилок.

Рис. 21. Приклад графічного візуалізатора для спостереження за помилками в ході навчання (n — номер ітерації)

Візуалізатори для інтерпретації результатів аналізу. Як на вході, так і на виході аналітичного процесу присутні деякі дані. Дані на вході зазвичай називаються вихідними. Передбачається, що вони мають властивості, містять закономірності, структура та особливості, виявлення і розуміння яких дозволяє отримати нові знання про досліджувані об’єкти. На виході також виявляються дані, які є результатами. На їх основі формулюються висновки і приймаються рішення щодо досліджуваної проблеми.

Природно, що аналітична обробка даних не дає готових відповідей на всі питання, потрібні аналітику, досліднику чи особі, яка приймає рішення. У процесах аналізу відбувається лише перетворення даних до уявлення, яке дозволяє побачити в них дещо важливе з точки зору дослідження та управління певним цільовим об’єктом або процесом. Тому між результатами аналізу та отриманими на їх основі знаннями та рішеннями лежить процедура інтерпретації результатів, яка найчастіше виявляється не менш складною і проблемною, ніж сам аналіз цільового об’єкта чи процесу.

Досвід аналітики підтверджує, що неправильна інтерпретація може не тільки знецінити найвдаліші результати аналізу, але і привести до спотворених помилкових висновків, що можуть спричинити на їх основі наступні неправильні управлінські рішення. Саме тому в аналітиці досить багато уваги приділяється візуалізації результатів аналізу, що дозволяє реалізувати їх інтерпретацію якомога ефективніше і звести до мінімуму можливість помилкових висновків чи рішень.

Досить часто, крім візуалізаторів загального призначення, до складу аналітичних програм і платформ включається набір спеціалізованих засобів візуалізації, пов’язаних із специфічними процесами для аналізу моделей, формою представлення їх результатів і цілями аналізу з врахуванням його особливостей.

Результати різних розрахунків доводять, що основною складністю в інтерпретації результатів аналізу є велика розмірність наборів даних у процесах оперування моделлю. У даному випадку найприйнятніший підхід той, що застосовує моделювання даних великої розмірності за допомогою вкладеного в багатовимірний простір різноманіття даних зменшеної розмірності. Наприклад, для зображення даних на екрані монітора найбільш природно використовувати два виміри. Адже людина здатна наочно уявляти не більше двох-трьох вимірів різноманітних даних, причому — обмеженого обсягу.

Щодо уявлення інформації великої розмірності, то принципово існує два основні способи опису відповідних даних. Перший полягає в побудові ієрархічної структури даних, тобто у разі необхідності розділення даних на класи, підкласи тощо, і другий — у скороченні розмірності вихідного простору даних. Практика застосування інструментів інтерпретації демонструє кілька типів візуалізаторів, поширених в аналітичній діяльності, а саме:

а) деревоподібні візуалізатори;

б) візуалізатори зв’язків;

в) карти.

Розглянемо стисло їх характеристику.

Можливості деревоподібних візуалізаторів. В дійсності багато методів, і алгоритми дейтамайнінгу оперують різними об’єктами і структурами, які організовано в упорядкуванні ієрархії. До таких методів і алгоритмів належать дерева рішень, асоціативні правила, деякі методи кластеризації та ін. В принципі, деревоподібні візуалізатори можуть використовуватися в тих додатках, де результати аналітичної обробки даних утворюють ієрархічні рівні і можуть бути розділені на предків і нащадків. Одним із базових понять в цьому розумінні є поняття «дерева» як категорії візуалізації.

Візуалізатори дерев. Слід визнати, що однією з найпопулярніших класифікаційних моделей є дерева рішень. Вони представляють собою ієрархічну послідовність правил на кшталт «якщо..., то...». Наприклад, класифікаційне правило може бути сформульовано таким чином: «Якщо значення ознаки X > 10, то об’єкт належить до класу А». У процесі побудови моделі генерується ієрархічна послідовність правил, що застосовуються до досліджуваної вибірки і розподіляють всі вхідні до неї об’єкти щодо заздалегідь визначених класів відповідно до визначених умов чи правил.

У ході послідовної інтерпретації результатів класифікації за допомогою дерев рішень використовуються візуалізатори, що відображають структуру дерева, а також сформульовані в ньому правила. Приклад дерева рішень для класифікаційного завдання про розподіл платників податків за категоріями уваги наведено на рис. 22. Для компактності класифікаційні ознаки платників позначені таким чином: ВП — вік підприємства, ГД — галузь діяльності, СП — спеціалізація, ОФ — наявність офшорних партнерів. При такому способі візуалізації дерева рішень вузли і листя представлено у вигляді прямокутників і розташовано в порядку їх ієрархічної підпорядкованості. У кожному вузлі зазначається чинне в ньому правило.

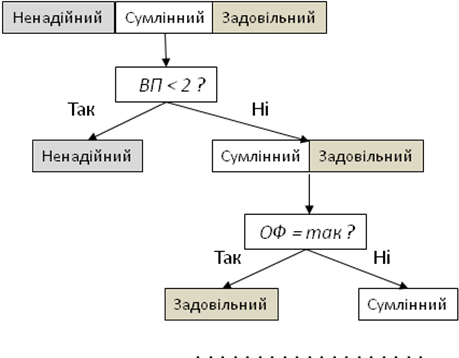
Рис. 22. Фрагмент дерева рішень класифікації ПП

Основна цінність методу дерев полягає не тільки в тому, що він дозволяє класифікувати об’єкти, але й в тому, що він описує їх властивості. Так, за деревом рішень можна оцінити ступінь подібності класів. Якщо для розпізнавання класів досить одного або двох правил, то об’єкти цих класів добре помітні: їх ознаки (або хоча б одна з них) сильно відрізняються. Якщо ж для розпізнавання класів потрібно декілька правил, класи розрізняються складніше: ознаки їх об’єктів ближчі (об’єкти більш подібні). Крім того, правила не тільки класифікують об’єкти, але й описують їх узагальнені властивості, пояснюють, за якою ознакою об’єкт віднесено до певного класу в ході процесу розпізнавання.

Візуалізація дерев асоціативних правил. Переважну більшість дерева рішень називають індуктивними, оскільки правила, з яких вони складаються, розбивають вихідну множину даних на підмножини, які відповідають класам. Поряд з індуктивними правилами в дейтамайнінгу широко використовуються так звані асоціативні правила. При цьому на відміну від індуктивних правил, які служать для розпізнавання об’єктів за належністю до певного класу, асоціативні правила встановлюють взаємний зв’язок між подіями в процесі класифікації, що може знайти застосування, наприклад, для розпізнавання ризиків.

Розглянемо, наприклад, класифікацію подій, що можуть представляти податкові ризики. Якщо подією А передбачено подію X, а подією В — подія Y, то асоціація між даними подіями записується у вигляді А → В і розуміється як: «Із А випливає В». При цьому подія А називається умовою, а подія В — наслідком. Якщо асоціація між А і В є правилом, це означає, що після здійснення події А, з великою ймовірністю відбувається подія В (тобто подія X у більшості випадків тягне за собою подію Y). Наскільки та чи інша асоціація є правилом, визначається шляхом аналізу досить великої кількості відповідних подій. Так, якщо було встановлено, що із 100 транзакцій, в яких з’являлася подія А, 95 транзакцій містять подію В (тобто ймовірність спільної появи А і В дорівнює 0,95 або 95%), то таку асоціацію з високим ступенем ймовірності можна вважати правилом.

Відповідне застосування асоціативні правила можуть знайти в організації контрольно-перевірочної роботи й аудиті, що досить актуально в процесах, наприклад, горизонтального аудиту платників податків. Якщо відомо, що подія X (можна припустити, що це проведення платником експортно-імпортних операцій) з великою ймовірністю тягне за собою подію Y (наприклад, партнер в офшорній зоні), то логічно інспектору, який контролює зовнішньоекономічну діяльність платника X, перевірити наявність офшорних партнерів Y.

Відповідний пошук і аналіз асоціативних правил дозволяє виявляти групи подій, які часто відбуваються разом, а це, в свою чергу, допомагає цілеспрямовано перевірити, в нашому випадку, в процесах податкового контролю і класифікації платників податків за категоріями уваги в частині зовнішньоекономічної діяльності наявність відповідних ризиків.

З метою підвищення ефективності інтерпретації результатів пошуку асоціативних правил доцільно використовувати уявлення класифікацій у вигляді дерев. Але на відміну від індуктивних правил у деревах рішень асоціативні правила не використовують ієрархію, оскільки пошук правил відбувається незалежно для всіх можливих асоціацій між ними. Один із можливих варіантів візуалізації асоціативних правил для вищенаведеного прикладу перевірки платників податків за допомогою дерева представлено на рис. 23. Кожен вузол утворено умовою, якому відповідає одне або кілька наслідків, асоціації з якими були виявлені у вихідному наборі транзакцій. Як умова, так і наслідок можуть бути утворені однією подією («експортно-імпортна операція») або комплексом подій («організація зовнішньоекономічної діяльності»). У кожному вузлі може бути передбачено виведення значень (наприклад, у %) щодо підтримки або оцінки достовірності відносно пов’язаної з ним асоціації.

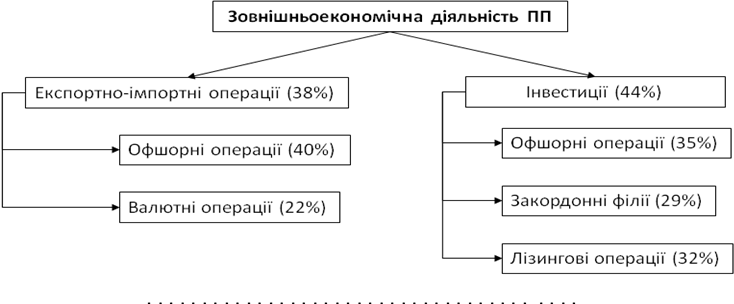
Рис. 23. Приклад дерева асоціативних правил класифікації ПП

Характеристика кластеризації. Слід визнати, що однією з найважливіших груп завдань дейтамайнінгу є кластеризація — це об’єднання об’єктів у групи на основі схожості їх ознак. Такі групи називаються кластерами. Попадання двох об’єктів в один кластер дозволяє припустити високу ступінь схожості їхніх властивостей, і навпаки, якщо об’єкти в результаті кластеризації потрапили до різних кластерів, то вважається, що вони суттєво відрізняються один від одного за своїми ознаками.

Як стандартний результат операцій кластеризації певної множини даних формується відповідна кількість кластерів. Одним з популярних видів кластеризації є ієрархічна кластеризація, яка, в свою чергу, містить два основні методи, а саме:

• метод агломеративної кластеризації — це, коли кластери формуються шляхом злиття кластерів меншого розміру в кластери більшого розміру в межах вибірки;

• метод розподільної кластеризаціі (дивідивної) — це, коли кластери більшого розміру поділяються на кілька кластерів меншого розміру щодо первинної множини.

Характерним для візуалізації результатів ієрархічної кластеризації є використання спеціального різновиду діаграм, які називаються дендрограмами. Дендрограма відображає ступінь близькості окремих об’єктів і кластерів, а також наочно представляє в графічному вигляді послідовність їх об’єднання чи поділу. Кількість рівнів дендрограми відповідає кількості кроків злиття або поділу кластерів. Приклад дендрограми наведено на рис. 24. У нижній частині рисунка розташована шкала, на якій відкладається відстань між об’єктами в просторі ознак схожості чи різниці.

Для прикладу дендрограма на рис. 24 будується таким чином. На першому кроці групуються об’єкти x₂ і х₃, утворюючи кластер {х₂, х₃} з мінімальною евклідовою відстанню, яка приблизно дорівнює 2. Потім об’єкти x₄ і x₅ групуються в інший кластер {x₄, x₅} з відстанню 4. Відстань між кластером {х₂, х₃} і {х₁} також виявляється рівною 2, що дозволяє згрупувати дані кластери на тому самому рівні, що і {x₄, х₅} — і нарешті, два кластери — {х₂, х₃, х₁} і {х₄, x₅} — групуються на найвищому рівні ієрархії кластерів з відстанню 6. У нашому випадку відстань може характеризувати наявність податкових ризиків.

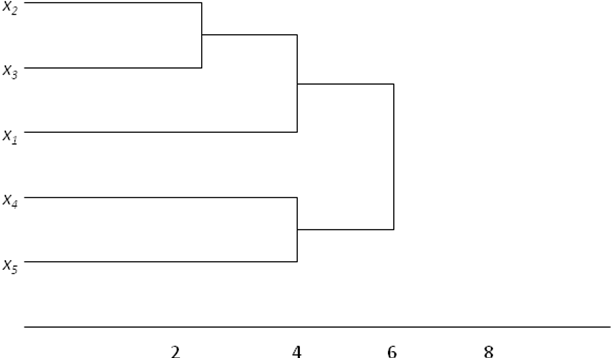
Рис. 24. Вигляд дендрограми класифікації ПП за податковими ризиками

Методи візуалізації зв’язків. Важливе значення для аналітики має дослідження характеру і ступеня взаємної залежності між різними об’єктами. Для такого аналізу можна використовувати такі методи візуалізації зв’язків, коли об’єкти представляються у вигляді певних графічних позначок чи об’єктів, а зв’язки між ними — у вигляді ліній, що з’єднують відповідні об’єкти. При цьому сила зв’язку, тобто ступінь взаємної залежності об’єктів, може представлятися різними способами. Найчастіше для цього використовують такі засоби, а саме:

• використання різної товщини ліній: чим сильніше зв’язок між об’єктами, тим товщі лінії для їх з’єднання (рис. 25, а);

• різний колір ліній, при цьому можуть обиратися відтінки певного спектра (рис. 25, б) за необхідності.

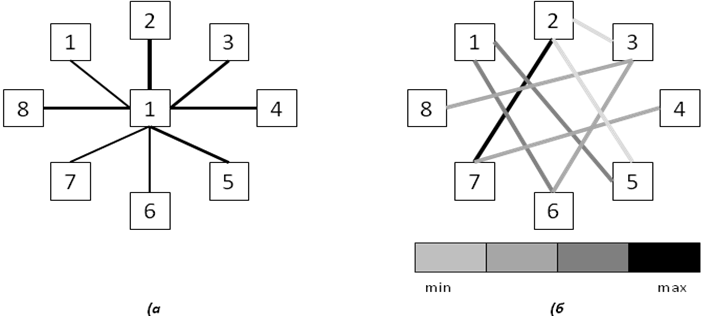
Рис. 25. Діаграми зв’язків між об’єктами: а — «зірка»; б — «мережа».

У разі необхідності в окремих випадках допускається одночасно використовувати і товщину, і колір, хоча такі діаграми більш складні для сприйняття і розуміння.

Інша можливість візуалізації пов’язана з різним розташуванням об’єктів на площині. У першому випадку відображаються зв’язки між одним обраним об’єктом, який розміщено у центрі, і всіма іншими (так звана, «зірка», рис. 25, а). У другому випадку візуалізуються всі попарні зв’язки між об’єктами (так звана «мережа», рис. 25, б). Якщо кількість об’єктів досить велика, кількість зв’язків збільшується, тому найчастіше аналізують тільки найсильніші або найслабкіші, накладаючи обмеження на позначення інтенсивності зв’язку або інші його характеристики.

Найчастіше об’єкти порівнюються між собою на основі певних ознак. Якщо ознак декілька, обирається спосіб розрахунку критерію зв’язку. Найчастіше метрика — тобто правило обчислення відстані в багатовимірному просторі ознак, а саме: евклідова відстань, відстань Манхеттена та ін.

Характерний приклад діаграми зв’язків між різними регіонами Україні представлено на рис. 26. Як ознаки в даному випадку використовуються: а) чисельність постійного населення, б) питома вага міського населення, в) зафіксована за останній період чисельність підприємців на 1000 осіб населення.

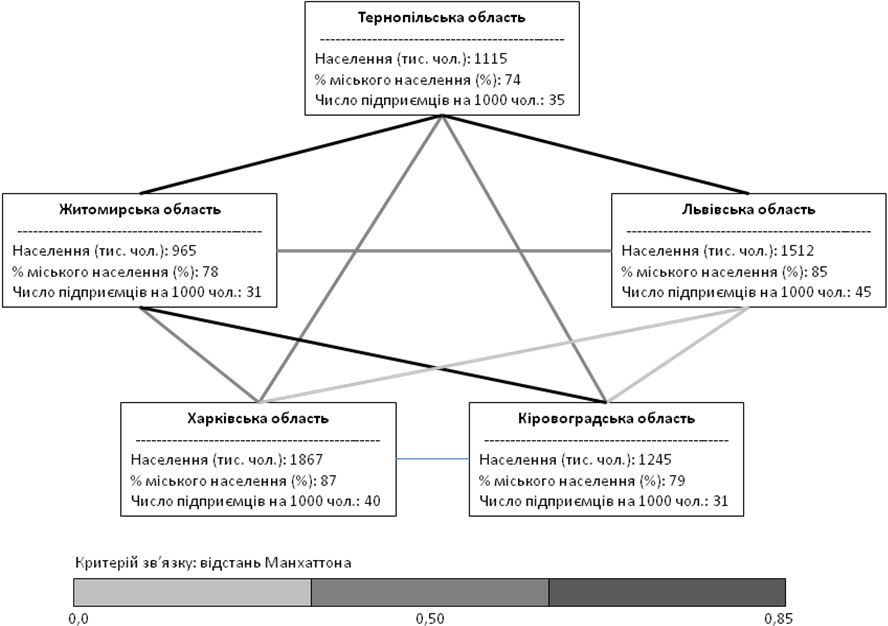
Рис. 26. Діаграми зв’язків між регіонами України

Загальний критерій зв’язку для наведеного прикладу обчислювався з використанням манхеттенівської відстані. Можна бачити, що Тернопільська та Житомирська області досить близькі за порівняльними ознаками (відстань дорівнює 0,79), а між Львівською та Кіровоградською областями, навпаки, розходження — найбільше (відстань — 0,18), що відображено лініями.

Візуалізація у вигляді карт. Карти дозволяють наочно представити дані, пов’язані з географічним розташуванням досліджуваних об’єктів і процесів. Це можуть бути демографічні або економічні дані (наприклад, розподіл показників чисельності населення або доходу на душу населення за різними регіонами), а також дані, що відображають активність підприємницької діяльності чи рівень податкових надходжень тощо.

Як приклад: у табл. 6 містяться дані про розподіл надходжень податку на доходи фізичних осіб для Західного регіону України (ЗРУ).

Таблиця 6