Вихідні дані для гістограми податкових надходжень
Діапазон тис. грн. |
10-20 |
20-30 |
30-40 |
40-50 |
50-60 |
60-70 |
70-80 |
80-90 |
90-100 |
Частота |
1 |
1 |
2 |
6 |
10 |
6 |
3 |
1 |
1 |
Можна побачити, що податкові надходження на суму від 10 до 20 тис. грн. спостерігалися тільки один раз, від 30 до 40 тис. — двічі і т. п. На основі отриманої таблиці будується гістограма (рис. 7), наприклад у стовпчиковому вигляді.
Стандартно по горизонтальній осі гістограми відкладаються значення податкових надходжень, а по вертикальній — кількість або частота спостережень, значення яких потрапили в заданий діапазон (тому іноді гістограму називають частотним полігоном у статистиці).
Наведена на рис. 7 гістограма показує, що найбільша кількість спостережень потрапила в діапазон 50 — 60 тис. грн. Таким чином, значення з даного діапазону можна розглядати як найвірогідніші. Цю інформацію використовують для відновлення пропущених значень при очищенні даних, для планування грошових надходжень у задачах фіскального прогнозування тощо.
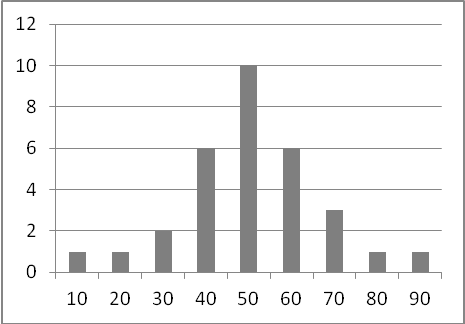
Рис. 7. Приклад гістограми розподілу податкових надходжень
Досить специфічним є застосування крайніх елементів гістограми, які представляють умовно рідкісні події — екстремальні високі або екстремальні низькі значення надходжень. Слід зазначити, що до діапазону 10 — 20 тис. грн. потрапило лише одне значення, отже, ймовірність такої події мала і його не варто включати до розгляду. Екстремальні низькі надходження податків можуть бути викликані винятковими ситуаціями, наприклад несприятливими умовами бізнесу для платника податків, потенціальними можливостями порушення податкового законодавства, проявами податкових ризиків. Можливості податкової аналітики щодо подібних даних розглядалися в розділі 3 даної НДР.
Особливий вид візуалізації належить до так званих нормованих гістограм, що дозволяє оперувати не значеннями спостережень, а їх ймовірностями. Для вищенаведеного прикладу кожен елемент гістограми ділиться на кількість спостережень, тобто в нашому випадку на 12 (число місяців у році). Ця ситуація розглядається на рис. 8, де вертикальна вісь дозволяє відображати ймовірності надходження певних сум податків.
Фактично, при такому підході висота стовпчика визначається не кількістю спостережень, що потрапили у відповідний діапазон, а ймовірністю попадання до нього. На рисунку видно, що ймовірність попадання значення до діапазону 50 — 60 тис. грн. становить приблизно 0,32, або 32%. Відповідно ймовірність появи значень у діапазоні 10 — 20 тис. грн. не перевищує 0,03, або 3%.
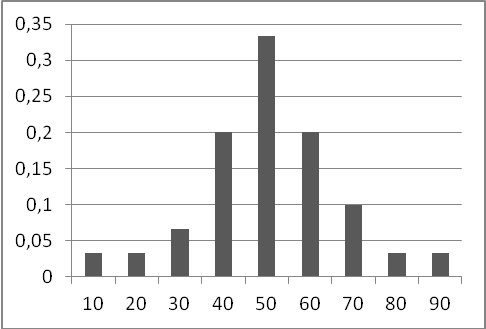
Рис. 8. Приклад нормованої гістограми податкових надходжень
Відповідним чином у нормованій гістограмі сума значень всіх її елементів повинна дорівнювати 1, оскільки сума ймовірностей всіх можливих подій (попадання значення до будь-якого діапазону) є 1. Застосування нормованих діаграм також можна рекомендувати як засіб відображення податкової аналітики, наприклад, для прогнозування податкових надходжень або оцінки податкових ризиків. Нажаль цей вид аналітики також не використовується у відображенні результатних звітних даних.
У процесі побудови гістограм аналітикам важливо надавати можливість завдання числа піддіапазонів, на яке розбиватиметься вихідний діапазон змінення величини (фактично це кількість стовпчиків гістограми). Тут існують різні рекомендації, наприклад: число піддіапазонів не повинно бути менше, ніж log2 № (log2 №-убрать, замінити на log2N) , де № (№-убрать, замінити на N)— кількість спостережень. На практиці можна скористатися таким емпіричним правилом. Кількість стовпчиків у гістограмі повинна бути такою, щоб у ній не утворювалися провали, різкі викиди або множинні піки. Вона повинна бути досить згладженою, щоб за нею можна було визначити характер розподілу спостережуваної величини. Практика показує, що досить часто хороший результат вдається отримати при використанні 10 — 15 стовпчиків у середньому.
Візуалізація статистики. Наступним поширеним засобом візуалізації, яке входить до складу більшості аналітичних програм, є інформація про статистичні характеристики досліджуваної вибірки. Вони зазвичай подаються в табличному вигляді і вказуються для кожного поля вибірки. Статистичні характеристики дозволяють формулювати гіпотези про поведінку даних і властиві їм закономірності, контролювати результати обробки даних на різних етапах аналітичного процесу. Типовий вид візуалізатора статистики представлено в табл. 2 для прикладу статистичної аналітики податкових надходжень.
Таблиця 2