1)Первообразная :

Первообрáзной^[1] данной функции f называют такую F, производная которой равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Теорема: Если F₁(x) и F₂(x) -первообразные для одной и той же функции f(x), то их разность есть величина постоянная.

Докозательство: По условию F'₁(x)=F'₂(x)=f(x) обозначим: Ф(x)= F₁(x) - F₂(x). Очевидно, Ф'(x) равняется нулю во всем промежутке (a,b), где определены первообразные F₁(x) и F₂(x). Для любых х₁, x₂ ,Î (a,b) по формуле Лагранжа Ф(х₁)-Ф(х₂)=Ф'(c)(b-a). но Ф'(c)=0, т.к. сÎ (a,b), следовательно Ф(х₁)=Ф(х₂). Это означает, что Ф(х) сохраняет постоянное значение на промежутке (a,b), т.е. F₁(x) - F₂(x)=С.

2)Неопределенный интеграл :

Множество всех первообразных от функции F(x)+C для f(x) называется неопределенным интегралом от функции f(x).

Свойства неопределенного интеграла :

1)Дифференциал от неопределенного интеграла равен подыантегральному выражению, а производная неопределенного интеграла равна подынтегральной функции :

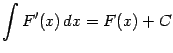
и

2)Нопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольно постоянной :

3)Постоянный множитель можно вынести за знак интеграла :

4)Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций :

5)(Инвариантность формулы интегрирования ). Если f(x)dx = F(x)+C,то и f(u)du=F(u)+C , где u=ФИ(x) – произвольная функция, имеющая непрерывную производную.

3)Таблица основных неопределенных интегралов :

4) Метод подведения под знак дифференциала :

Метод подведения под знак дифференциала основан на равенстве . То есть, главной задачей является приведение подынтегральной функции к виду .

Примеры :

.

, где

5) Интегри́рование по частя́м —Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций ,то справедливы следующие формулы

Возможно дифференцирование :

Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:

Операция интегрирования обратна дифференцированию:

После перестановок:

Примеры:

• 

• 

6)Интегрирование рациональных дробей :

Разложение дробей позволяет интегрировать рациональные функции. Любая рациональная функция может быть представлена в виде суммы некоторого многочлена и некоторого числа дробных функций. Каждая дробь имеет знаменатель в виде многочлена первой или второй степени, причём многочлен в знаменателе, в свою очередь, также может быть возведён в некоторую положительную целую степень. Если знаменатель является многочленом первой степени, возведённым в некоторую целую положительную степень, то числитель дроби является постоянным числом. Если знаменатель является многочленом второй степени (или некоторой целой положительной степенью такого многочлена), то числитель является многочленом первой степени.

Соответственно, любой многочлен может быть разложен по формуле

Следовательно, дробь, знаменателем которой является многочлен, может быть разложена следующим образом:

Метод неопределённых коэффициентов ― метод, используемый в математике для нахождения искомой функции в виде точной или приближённой линейной комбинации конечного или бесконечного набора базовых функций. Указанная линейная комбинация берётся с неизвестными коэффициентами, которые определяются тем или иным способом из условий рассматриваемой задачи.

7) Интегрирование выражений, содержащих квадратный трехчлен :

Рассмотрим интеграл , содержащий квадратный трехчлен в знаменателе подынтегрального выражения. Такой интеграл берут также методом подстановки, предварительно выделив в знаменателе полный квадрат. Покажем это на примерах.

Пример 12. Вычислить .

Решение. Преобразуем , выделяя полный квадрат по формуле . Тогда ;

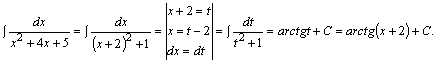
8) Интегрирование некоторых тригонометрических:

Интегралы этого вида вычисляются с помощью подстановки . Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.

, 

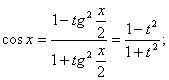
Тогда 

Описанное выше преобразование называется универсальной тригонометрической подстановкой.

  Пример.

9) Интегрирование некоторых иррациональных функций

Не от всякой иррациональной функции интеграл выражается через элементарные функции. Рассмотрим те функции, интегралы от которых с помощью подстановок приводятся к интегралам от рациональных функций и интегрируются в элементарных функциях.

Пример.

Вычислить интеграл .

Решение.

Выполним подстановку , , , тогда

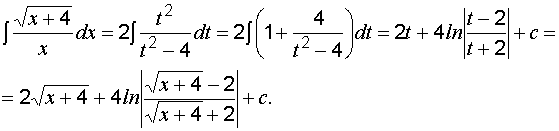
10) Нахождение площади криволинейной трапеции :

Пусть на отрезке [a,b] задана непрерывная функция y=F(x)>=0. Фигура, ограниченная сверху графиком функции y=f(x), снизу – осью Ох, сбоку – прямыми x=a и x=b, называется криволинейной трапецией.

Пусть требуется найти площадь плоской фигуры (рис.), ограниченной графиком функции у = f (х), непрерывной и  неотрицательной на отрезке [a ; b], и отрезками прямых . Разобьем [a ; b] точками

Произведение    даст площадь  прямоугольника, имеющего основание и высоту , а сумма — приближенно площадь S криволинейной трапеции aABb.  Отсюда, как и в предыдущей задаче,  

Нахождение работы переменной силы :

Пусть точка движется по оси Ох под действием силы, проекция которой на ось Ох есть функция f от х. При этом мы будем предполагать, что f есть непрерывная функция. Под действием этой силы материальная точка переместилась из точки М (а) в точку М (b) (рис. 1, а). Покажем, что в этом случае работа А подсчитывается по формуле

(1)

Работа силы на всем отрезке [а; b] равна сумме работ этой силы на полученных отрезках.

Точность приближенного равенства тем выше, чем короче отрезки, на которые разбит отрезок [а;b] Естественно, что это приближенное равенство переходит в точное, если считать, что n→∞:

Следовательно работа переменной силы F, величина которой есть непрерывная функция F = F(x), действующей на отрезке [a,b] , равна определенному интегралу от величины F(x) силы, взятому по отрезку [а,b]

11)Определенный интеграл :

1. С помощью точек х₀=а, x_1, х_{2, ...,} х_n = В (х₀ <x₁ < ...< х_n) разобьем отрезок [а, b] на n частичных отрезков [х₀;х₁], [x₁; х₂],..., [х_n-1,х_n]

2. В каждом частичном отрезке [x_i-1;x_i], i = 1,2,...,n выберем произвольную точку с_i є [x_i-1; x_i] и вычислим значение функции в ней, т. е. величину ƒ(с_i).

3. Умножим найденное значение функции ƒ (с_i) на длину ∆x_i=x_i-x_i-1 соответствующего частичного отрезка: ƒ (с_i) • ∆х_i.

4. Составим сумму S_n всех таких произведений:

Сумма вида (35.1) называется интегральной суммой функции у = ƒ(х) на отрезке [а; b].

Если при этом интегральная сумма S_n имеет предел I, который не зависит ни от способа разбиения отрезка [а; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = ƒ(х) на отрезке [а; b] и обозначается Таким образом,

Геометрический смысл :

Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен площади криволинейной трапеции, прилегающей к оси Ox и ограниченной кривой у=f(x)

Если f(x) непрерывна и положительна на [a, b], то интеграл

Пусть на отрезке [a,b] задана непрерывная функция y=F(x)>=0. Фигура, ограниченная сверху графиком функции y=f(x), снизу – осью Ох, сбоку – прямыми x=a и x=b, называется криволинейной трапецией.

Условия существования определенного интеграла :

Если бы функция f(x) была в промежутке [a, b] неограниченна, то – при любом разбиении промежутка на части – она сохранила бы подобное свойство хоть в одной из частей.

12)Свойства определенного интеграла :

1)Линейность. Если функции y = f(x), y = g(x) интегрируемы по отрезку [a,b] , то по этому отрезку интегрируема их линейная комбинация A f(x) + B g(x) (A, B = const), и .

2)Аддитивность. Если y = f(x) интегрируема по отрезку [a,b] и точка c принадлежит этому отрезку, то .