62

Дано приближенное число и относительная погрешность числа. Записать число с явным указанием погрешности.

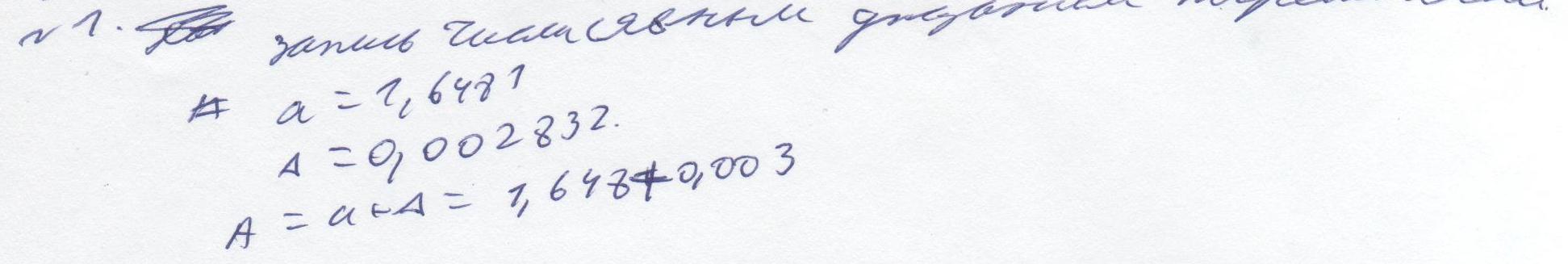
1. Известна абсолютная или относительная погрешность приближенного числа. Определить количество верных цифр числа, используя определение количества верных цифр.

Если положительное приближенное число   имеет относительную погрешность  , то количество верных знаков n данного числа можно определить по формуле

и в качестве n взять ближайшее целое к   число.

x = 42.221,  = 0.5%

 Найдем количество верных цифр числа x:

Отсюда n = 3

Дано число a = 547.78, определенное с абсолютной погрешностью  . Определить количество верных цифр числа а.

Решение:

1) Найдем относительную погрешность числа

2) Найдем количество верных цифр

Отсюда n = 4, a = 547.8

2. Дана функция f(a,b,c). Значения переменных указаны со всеми верными цифрами. Оценить погрешность результата, используя общую формулу погрешностей.

Общая формула вычисления погрешности

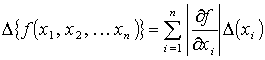
Задача 2.

Записать формулу для оценки  абсолютной погрешностей функции трех переменных:

, если 

Решение:

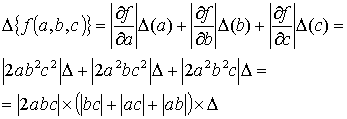
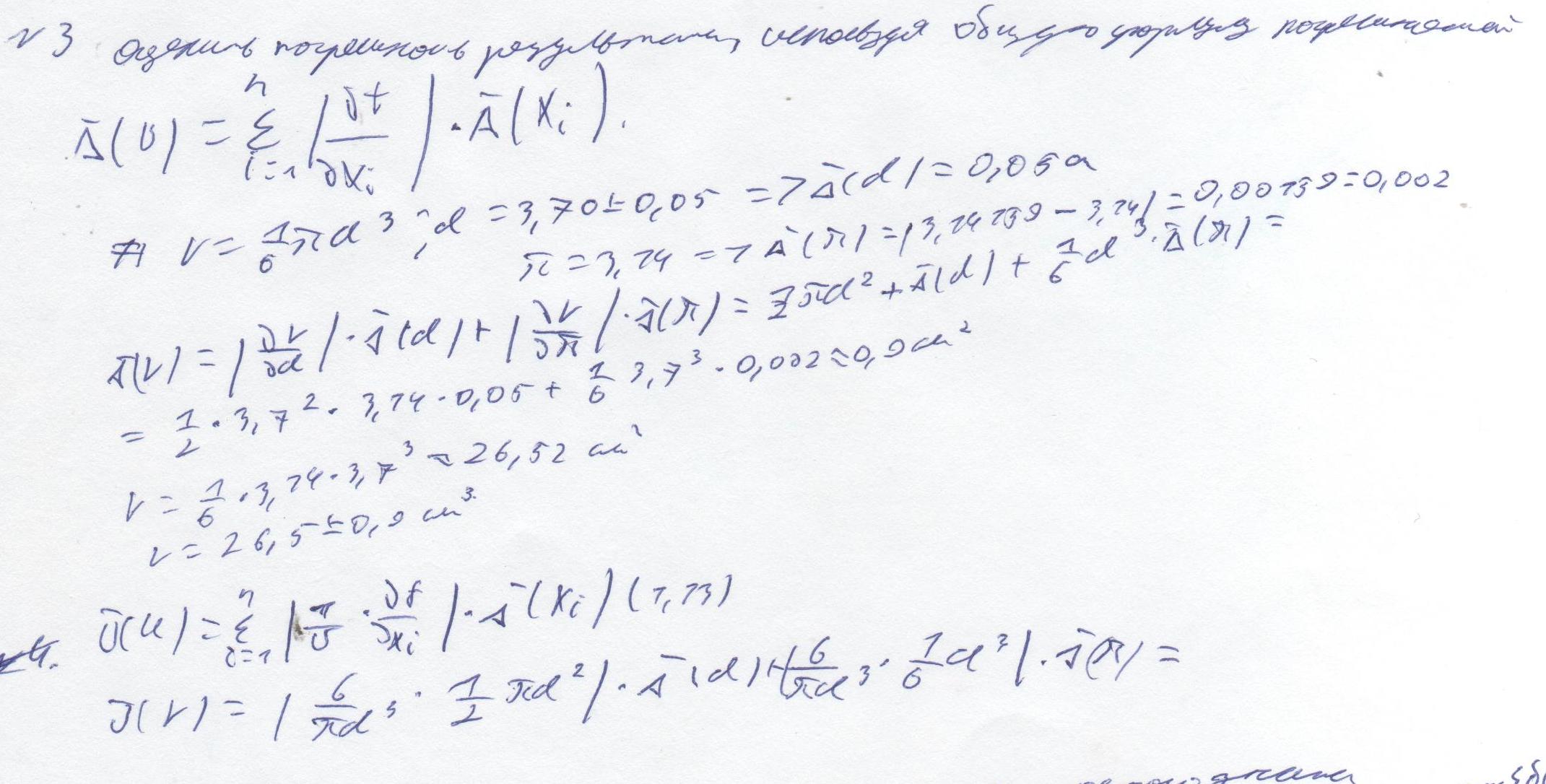
3. Дана функция f(a,b,c). Значения переменных указаны со всеми верными цифрами. Оценить погрешность результата, используя оценки погрешностей для арифметических операций.

Погрешности арифметических действий

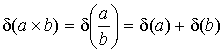
4. Перечислить все элементы главного окна matlab, их назначение и особенности.

http://orloff.am.tpu.ru/matlab/index.htm лабораторная №1. – 3.интерфейс Матлаб

Рабочая среда MatLab содержит следующие элементы:

-панель инструментов с кнопками и раскрывающимся списком;

-окно с вкладками Launch Pad и Workspace, из которого можно получить доступ к различным модулям ToolBox и к содержимому рабочей среды;

-окно с вкладками Command History и Current Directory, предназначенное для просмотра и повторного вызова ранее введенных команд, а также для установки текущего каталога;

-командное окно, в котором находится приглашение к вводу » и мигающий вертикальный курсор;

-строку состояния.

Если в рабочей среде MatLab отсутствуют некоторые окна, то следует в меню View выбрать соответствующие пункты: Command Window, Command History, Current Directory, Workspase, Launch Pad.

5. Перечислить все арифметические операторы matlab (название, обозначение) с указанием их приоритета. Привести примеры для каждого оператора.

В отличие от большинства языков программирования в системе MATLAB практически все операторы являются матричными, т. е. предназначены для выполнения операций над матрицами. Cписок арифметических операторов и синтаксис их применения:

Функция	Название Оператора	Синтаксис
Plus	Плюс +	М1+М2
Uplus	Унарный плюс +	+М
Minus	Минус	М1-М2
Uminus	Унарный минус	-М
Mtimes	Матричное умножение *	М1*М2
Times	Поэлементное умножение массивов .*	А1.*А2
Mpower	Возведение матрицы в степень	М1^х
Power	Поэлементное возведение массива в степень	А1.^х
Mldivide	Обратное (справа налево) деление матриц	M1\M2
Mrdivide	Деление матриц слева направо	М1/М2
Ldivide	Поэлементное деление массивов справа налево	А1.\А2
Rdivide	Поэлементное деление массивов слева направо	А1 . /А2
Kron	Тензорное умножение Кронекера	kron(X.Y)

При работе с массивом чисел установлены следующие уровни приоритета: уровень 1: поэлементное транспонирование (.'), поэлементное возведение в степень (.^), эрмитово сопряженное транспонирование матрицы ('), возведение матрицы в степень (^);

уровень 2: унарное сложение (+), унарное вычитание (-);

уровень 3: умножение массивов (.*), правое деление (./), левое деление массивов (.\), умножение матриц (*), решение систем линейных уравнений - операция (/), операция (\);

уровень 4: сложение (+), вычитание (-);

уровень 5: оператор формирования массивов (:).

Внутри каждого уровня операторы имеют равный приоритет и вычисляются в порядке следования слева направо. Заданный по умолчанию порядок следования может быть изменен с помощью круглых скобок.