Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:математика экзамен.docx

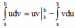 (4)
(4)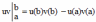
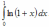
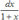 и
v=∫dv=∫dx=x. Применяя (4), получаем
и
v=∫dv=∫dx=x. Применяя (4), получаем