Можно показать, что производная Фреше, в том случае, когда она существует, совпадает с производной Гато.

20.

Во многих задачах функция  y(x) задана невным образом. Например, для приведенных ниже функций

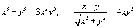
невозможно получить зависимость y(x) в явном виде.  Алгоритм вычисления производной  y'(x) от неявной функции выглядит следующим образом:

• Сначала необходимо продифференцировать обе части уравнения по отношению к x, предполагая,  что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции;

• Решить полученное уравнение относительно производной  y'(x).

21

Частной производной от функции 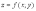  по независимой переменной   называется производная

, вычисленная при постоянном  .

Частной производной по y называется производная  , вычисленная при постоянном  . Для частных производных справедливы обычные правила и формулы дифференцирования.

22

Дифференцирование функций, заданных параметрически

Пусть функции x = (t) и y = ψ(t) определены на некотором отрезке [α, β]. Переменную t будем называть параметром.

Если x = (t) взаимно однозначна на отрезке [α, β], то она имеет обратную функцию t(x) =  ^{− 1} (x). Подставляя ее в равенство y = ψ(t), видим, что переменная yявляется сложной функцией переменной x:

 

y   =   ψ( − 1 (x) )   ≡   f(x) .

 

В этом случае говорят, что функция y = f(x) задана параметрически уравнениями

 

   x = (t) y = ψ(t)

(1)

 

где t  [α, β].

Производная первого порядка функции, заданной параметрически

24

Дифференциал высшего порядка функции одной переменной [править]

Для функции, зависящей от одной переменной 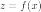   второй и третий дифференциалы выглядят так:

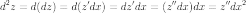
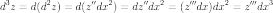
Отсюда можно вывести общий вид дифференциала n-го порядка от функции   :

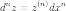
При вычислении дифференциалов высших порядков очень важно, что 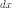  есть произвольное и не зависящее от   , которое при дифференцировании по    следует рассматривать как постоянный множитель.

Дифференциал высшего порядка функции нескольких переменных [править]

Если функция 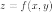   имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так:  .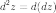

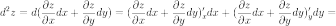
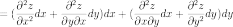
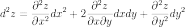
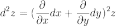
Символически общий вид дифференциала n-го порядка от функции 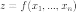  выглядит следующим образом:

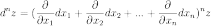
26

Формула Тейлора

Пусть функция f(x) определена в некоторой окрестности точки x₀ и n раз дифференцируема в точке x₀.   Многочлен

 

Pn(x)   =    n ∑ k = 0    f (k) (x0) k!    (x − x0)k

 

называется многочленом Тейлора n–го порядка функции f(x) с центром в точке x₀ .

Если функция f(x) является многочленом степени k, то при всех n ≥ k справедливо равенство

 

f(x) = Pn(x)

 

Если функция f(x) не является многочленом , то при всех n имеем f(x) ≠ P_n(x) и тогда

 

f(x) = Pn(x) + Rn + 1(x).

(1)

 

Это равенство называется формулой Тейлора.  В ней R_{n + 1}(x) — некоторая функция, называемая остаточным членом формулы Тейлора

Если x₀ = 0, то формулу Тейлора называют иногда формулой Маклорена. В этой связи рекомендуем прочитать раздел “История”.

Полезную информацию об остаточном члене формулы Тейлора R_{n + 1}(x) дают следующие две теоремы. Они уточняют уточняют формулу (1).

Теорема 1 (Пеано). Пусть функция f(x) имеет в точке x₀ производные до n–го порядка включительно. Тогда

Rn + 1(x) = o( (x − x0)n ) ,

 

27