
- •Геометрическая интерпретация комплексного числа
- •Векторное произведение векторов
- •Можно показать, что производная Фреше, в том случае, когда она существует, совпадает с производной Гато.
- •Дифференцирование функций, заданных параметрически
- •Производная первого порядка функции, заданной параметрически
- •Формула Тейлора
- •Формула интегрирования по частям в определенном интеграле
1
Комплексным числом z называется пара (x, y) действительных чисел x и y. При этом равенство, сумма и произведение упорядоченных пар, а также отождествление некоторых из них с действительными числами определяются следующим образом:
1) два комплексных числа z1 = (x1, y1) и z2 = (x2, y2) называются равными, если x1 = x2 и y1 = y2;
2) суммой комплексных чисел z1 и z2 называется комплексное число z вида
z = (x1 + x2, y1 + y2);
3) произведением комплексных чисел z1 и z2 называется комплексное число
z = (x1x2 - y1y2, x1y2 + x2y1);
4)
множество комплексных чисел 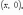
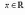 ,
отождествляется с множеством действительных
чисел R.
,
отождествляется с множеством действительных
чисел R.
Разностью комплексных чисел z1 и z2 называется комплексное число z такое, что z2 + z = z1, откуда находим z = z1 - z2 = (x1 - x2, y1 -y2).
Частным комплексных
чисел z1 и z2 называется
комплексное число z такое,
что 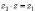 .
Отсюда находим
.
Отсюда находим
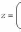
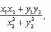
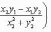
Комплексное
число (0, 1) обозначается символом i =
(0, 1). Тогда 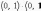
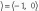 ,
т. е. i2 =
-1. Произвольное комплексное число z можно
записать в виде
,
т. е. i2 =
-1. Произвольное комплексное число z можно
записать в виде
z = (x, y) = (x, 0) + (0, y) = (x, 0) + (0, 1)(y, 0) = x + iy.
Эта
запись называется алгебраической
формой комплексного
числа. Комплексное число 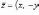
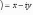 называетсясопряженным по
отношению к комплексному числу z =
(x, y)
= x + iy.
называетсясопряженным по
отношению к комплексному числу z =
(x, y)
= x + iy.
2
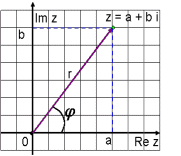
Геометрическая интерпретация комплексного числа
Всякое комплексное число z = (x, y) можно изобразить как точку на плоскости с координатами x и y. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy -мнимой.
Расстояние r точки z от нулевой точки, т. е. число
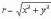
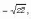
называется модулем комплексного числа z и обозначается символом |z|.
Число
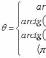

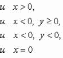
называем аргументом комплексного
числа z и
обозначаем символом θ =
arg z.
При заданном r углы,
отличающиеся на 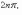
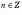 ,
соответствуют одному и тому же числу.
В этом случае записываем
,
соответствуют одному и тому же числу.
В этом случае записываем 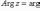
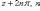
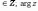 называем главным
значениемаргумента.
называем главным
значениемаргумента.
Числа r и θ называют полярными координатами комплексного числа z. В этом случае
z = (x, y) = (r cos θ, r sin θ) = r(cos θ + i sin θ)
называется тригонометрической формой комплексного числа.
Если z1 = (r1 cos θ1, r1 sin θ1), z2 = (r2 cos θ2, r2 sin θ2), то
z1z2 = (r1r2 cos(θ1 + θ2), r1r2 sin(θ1 + θ2)),
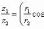
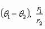
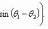
3
Действия с комплексными числами, заданных в тригонометрической форме
|
Запись
комплексного числа z
= a + bi в
виде z=r
Модуль
комплексного числа: r= Аргумент
комплексного числа:cos
=ra |
Свойство
умножения: Произведение
двух комплексных
чисел z1=r1 cos
cos 1+isin
1
1+isin
1 и z2=r2
cos
2+isin
2
будет
комплексное число
вида z1
и z2=r2
cos
2+isin
2
будет
комплексное число
вида z1 z2=r1
r2
cos(
1+
2)+isin(
1+
2)
z2=r1
r2
cos(
1+
2)+isin(
1+
2)
Свойство деления: Частное двух комплексных чисел z1=r1 cos 1+isin 1 и z2=r2 cos 2+isin 2 будет комплексное число вида z2z1=r2r1 cos( 1− 2)+isin( 1− 2)
Свойство возведение в степень: Степень комплексного числа z=r cos +isin будет комплексное число вида r cos +isin n=rn cosn +isinn
Свойство
извлечения корня: Корень
из комплексного числа z=r
cos
+isin
будет
комплексное число
вида 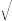 nr
cos
+isin
=
nr
cos
+isin
=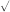 nr
nr cosn
cosn +2
+2 k+isinn
+2
k
k+isinn
+2
k
 k=0;1;2;
k=0;1;2; ;n−1
;n−1
Формула Муавра : cos +isin n=cosn +isinn
8
Матрицей
размера m x n называется прямоугольная
таблица чисел, содержащая m строк и n
столбцов.
Числа,
составляющие матрицу, называются
элементами матрицы. Матрицы обозначаются
прописными (заглавными) буквами латинского
алфавита, например, A, B, C,….
Для
обозначения элементов матрицы используются
строчные буквы с двойным индексом,
например: aij, где
i - номер строки, j - номер столбца.
Две
матрицы A и B одного размера называются
равными, если они совпадают поэлементно,
aij =
bij для
любых i=1,2,…m; j=1,2,…n, виды
матриц. Матрица,
состоящая из одной строки, называется
матрицей (вектором)- строкой, а из одного
столбца - матрицей (вектором)- столбцом:
Элементы матрицы aij,
у которых номер столбца равен номеру
строки называются диагональными и
образуют главную диагональ матрицы.
Для квадратной матрицы главную диагональ
образуют элементы a11,
a22,…,ann.
Если все недиагональные элементы
квадратной матрицы равны нулю, то матрица
называется диагональной.
Операции
над матрицами Над
матрицами, как и над числами, можно
производить ряд операций, причем
некоторые из них аналогичны операциями
над числами, а некоторые - специфические. 1.
Умножение матрицы на число. Произведение
матрицы А на число  называется
матрица B=
называется
матрица B= A,
элементы которой bij=
A,
элементы которой bij= aij для
i=1,2,…m; j=1,2,…n Следствие: Общий множитель
всех элементов матрицы можно выносить
за знак матрицы.
В
частности, произведение матрицы А на
число 0 есть нулевая матрица.
2.
Сложение матриц. Суммой
двух матриц А и В одинакового размера
m
aij для
i=1,2,…m; j=1,2,…n Следствие: Общий множитель
всех элементов матрицы можно выносить
за знак матрицы.
В
частности, произведение матрицы А на
число 0 есть нулевая матрица.
2.
Сложение матриц. Суммой
двух матриц А и В одинакового размера
m называется
матрица С=А+В, элементы которой
cij=aij+bij для
i=1,2,…m; j=1,2,…n (т.е. матрицы складываются
поэлементно).
3.
Вычитание матриц. Разность
двух матриц одинакового размера
определяется через предыдущие операции:
A-B=A+(-1)∙B.
называется
матрица С=А+В, элементы которой
cij=aij+bij для
i=1,2,…m; j=1,2,…n (т.е. матрицы складываются
поэлементно).
3.
Вычитание матриц. Разность
двух матриц одинакового размера
определяется через предыдущие операции:
A-B=A+(-1)∙B.
9
ОБРАТНАЯ
МАТРИЦА.РАНГ МАТРИЦЫ. Понятие
обратной матрицы вводится только
для квадратных
матриц.
Матрица  называется
обратной матрицей для квадратной
матрицы
называется
обратной матрицей для квадратной
матрицы  ,
если
,
если 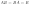 .
Если A –
квадратная матрица, то обратной для
неё матрицей называется матрица,
обозначаемая A-1 и
удовлетворяющая условию
.
Если A –
квадратная матрица, то обратной для
неё матрицей называется матрица,
обозначаемая A-1 и
удовлетворяющая условию 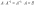 .
Для того чтобы квадратная матрица A имела
обратную, необходимо и достаточно, чтобы
её определитель был отличен от нуля. Из
определения обратной матрицы следует,
что матрица
.
Для того чтобы квадратная матрица A имела
обратную, необходимо и достаточно, чтобы
её определитель был отличен от нуля. Из
определения обратной матрицы следует,
что матрица  является
обратной для матрицы
является
обратной для матрицы 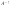 ,
то есть
,
то есть  .
Про матрицы
.
Про матрицы  и
и  можно
говорить, что они обратные друг другу
или взаимно обратны.
Итак,
чтобы найти обратную матрицу нужно:
1.Найти
определитель матрицы A.
2.Найти
алгебраические дополнения Aij всех
элементов матрицы A и составить матрицу
можно
говорить, что они обратные друг другу
или взаимно обратны.
Итак,
чтобы найти обратную матрицу нужно:
1.Найти
определитель матрицы A.
2.Найти
алгебраические дополнения Aij всех
элементов матрицы A и составить матрицу ,
элементами которой являются числа
Aij.
3.Найти
матрицу, транспонированную полученной
матрице
,
и умножить её на
,
элементами которой являются числа
Aij.
3.Найти
матрицу, транспонированную полученной
матрице
,
и умножить её на 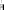 –
это и будет
–
это и будет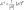 Свойства
обратной матрицы
Свойства
обратной матрицы
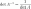 ,
где det обозначает определитель.
,
где det обозначает определитель.для любых двух обратимых матриц A и B.
где * обозначает транспонированную матрицу.
для любого коэффициента
 .
.
Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если существует, то x = b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе. Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от
10

 cos
cos +isin
+isin
 называется
тригонометрической формой комплексного
числа.
называется
тригонометрической формой комплексного
числа.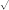 a2+b2
a2+b2  sin
=rb
sin
=rb