Критерій Міхайлова.

Заменим   , где ω — угловая частота колебаний, соответствующих чисто мнимому корню данного характеристического полинома.

Критерий: для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы кривая Михайлова, построенная в координатах  , проходила последовательно через n квадрантов.

Критерій Найквіста. Дозволяє зробити висновок про стійкість замкненої системи за годографом передавальної функції тієї ж САК із розірваним зворотнім зв’язком.

Повинні виконуватися умови:

• Правильний дріб W(s).

• Багаточлени чисельника і знаменника ПФ не мають співпадаючих коренів у правій півплощині.

• Число полюсів W(s) у правій півплощині дорівнює k.

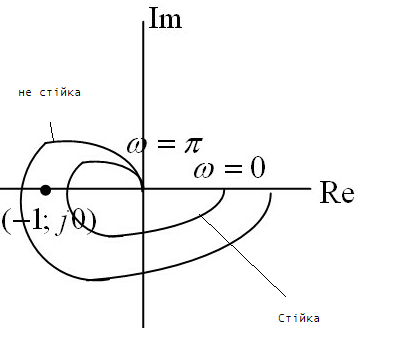
Для стійкості замкненої системи необхідно та достатньо, щоб при зміні w від 0 до нескінченності точки W(jw) робила рівно k півобертів навколо критичної точки з координатами (-1; j0), або що те саме , годограф W(jw) рівно k/2 рази охоплював критичну точку.

Визначення стійкості САР за ЛАЧХ та ЛФЧХ. Аналогічно до діаграм БОДЕ.

Бажана лачх

Передавальна функція САК – це відношення вихідної величини динамічної системи до вхідної, записаних у операційній формі при нульових початкових умовах.

Ланка САР – елемент САР, що розглядається з точки зору його динамічних властивостей і відбиває фізичні властивості реальних органів і їх частин, або сукупності органів в передаванні або перетворенні в прямому напрямку сигнал.

Пропорційна ланка САР – в якій в кожний момент часу існує пропорційність між вихідною та вхідною величинами.

Х_вих(t)=K X_вх(t)

Де К – коефіцієнт пропорційності

Передавальна функція

W(s)=K

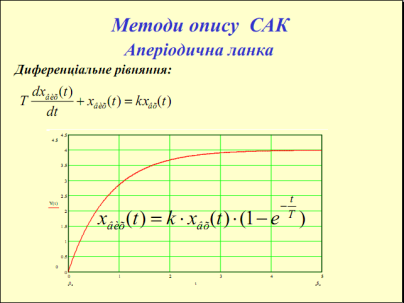
Аперіодична ланка(інерційна) – в якій при подачі на вхід ступінчастої дії вихідна величина аперіодично прямує до нового усталеного значення.

Передавальна функція

W(s)=K/(Тs+1)

Де К – коеф передачі, Т – постійна часу.

Коливальна ланка – в якій при одержанні на вході ступінчастої дії вихідна величина прямує до нового сталого значення здійснюючи загасаючі коливання.

Передавальна функція

W(s)=K/(Т²s²+2ξТs +1)

Де К – коеф передачі, Т – постійна часу, ξ – коеф коливальності.

Диференціююча ланка САР – в якій вихідна величина пропорційна швидкості зміни вхідної.

Передавальна функція

W(s)=Ks

Інтегруюча ланка САР – в якій швидкість зміни вихідної величини пропорційна вхідній, тобто вихідна величина пропорційна інтегралу за часом від вхідної величини.

Передавальна функція

W(s)=K/s

Структурна схема САР – Умовне графічне зображення системи диференційних рівнянь, яке описує динаміку елементів САР і системи вцілому.

Еквівалентні перетворення структурних схем – дозволяють одержати одно контурну схему і її передавальну функцію.

Аперіодичний перехідний процес

Коливальний перехідний процес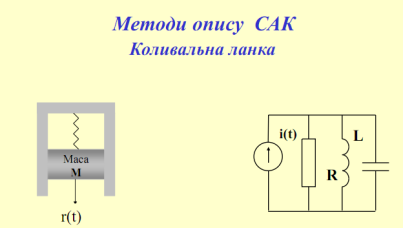

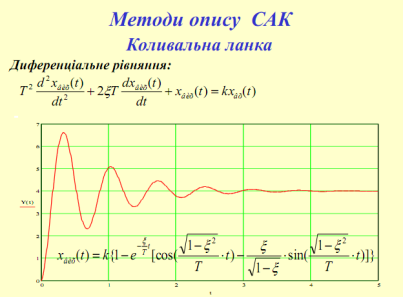
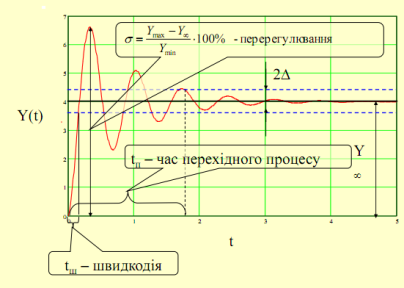
Гармонійний коливальний процес характеризується:

• швидкодією

• часом перехідного процесу

• пере регулюванням

• величиною періоду коливань Т=2П/ W

• Логарифмічним дикриментом затухання D=ln(A_n/A_n+1)

• число коливань М за час перехідного процесу М=2…3

Постійна часу – характеристика експоненціального процесу, що показує час через який амплітуда перехідного процесу зменшиться в е раз.

Статична похибка системи – відхилення керованої величини в сталому стані.

Динамічна похибка – відхилення керованої величини в перехідному процесі від заданого номінального значення.

Пряме перетворення Лапласа

Типова вхідна дія – пробні дії близькі до найбільш несприятливих зі всієї різноманітності реальних дій для конкретної системи.

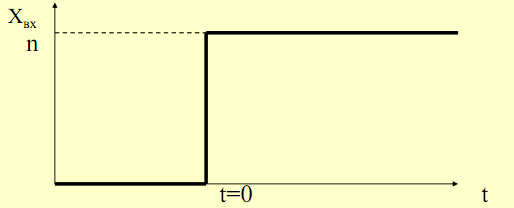
Ступінчаста дія – дія відсутня при t<0 і зберігає постійні значення при t≥0, що відповідає математичному запису.

0 при t<0

n при t≥0

Одиничний імпульс – імпульс нескінченно малої протяжності і нескінченно великої амплітуди.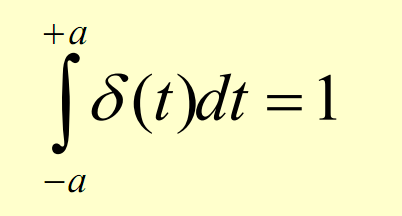

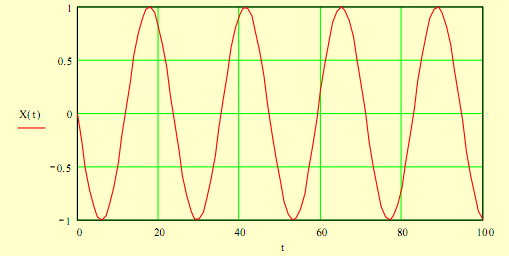
Гармонійна дія – дія , що визначається виразом:

Нелілійні ланки САР з обмежено-нелінійними х-ками

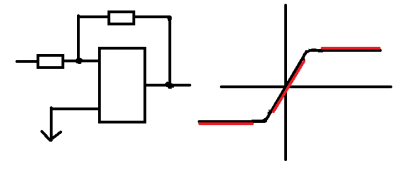
Нелілійні ланки САР з зоною нечутливості.

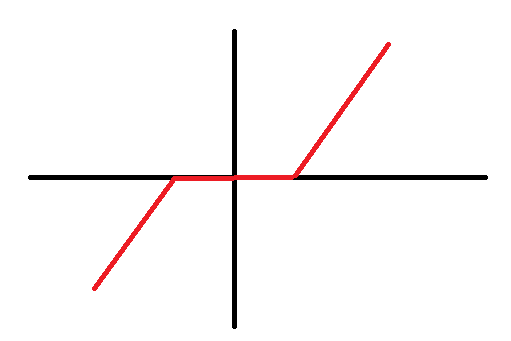
Нелілійні ланки САР з х-ками сухого тертя або зазору. Нелілійні ланки САР з релейними ха-ками.

Нелілійні ланки САР з х-ками у вигляді петлі гістерезису.

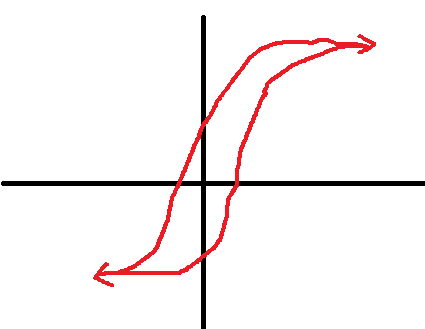
Поняття "бажана ЛАЧХ"

Рівняння стану - Уравнение состояния описывает инерционность динамического объекта.

Поняття робастності – організовує малу зміну виходу замкнутої системи керування при малій зміні об’єктів керування.

Аналіз робастності - функція чутливості залежність динамічних властивостей системи автоматичного керування (САК) від будь-яких відхилень її параметрів і характеристик від значень, взятих за початкові. 

Суттєво нелінійні системи відносяться елементи, характеристики яких мають різкі переломи, або розриви. Прикладами таких елементів є механічні з’єднання з люфтом, вузли механічних систем з сухим тертям, підсилювачі з насиченням, магнітні матеріали з петлею гістерезисну, релейні елементи та ін.

Нелінійні ланки САР, що мають обмежено-нелінійні характеристики

Нелінійні ланки САР, що мають характеристики з зоною нечутливості

Нелінійні ланки CAP, що мають характеристики сухого тертя або затору

Нелінійні ланки CAP, що мають релейні характеристики

Нелінійні ланки CAP. що мають характеристики у вигляді нетлі гістерезіса

Перетворення нелінійних структурних схем

Гармонійна лінеаризація

Метод фазових траєкторій

Зі зміною часу t точка М рухається по траєкторії, званої фазовою траєкторією. Якщо змінювати початкові умови отримаємо сімейство фазових траєкторій, званих фазовим портретом. Фазовий портрет визначає характер перехідного процесу в нелінійній системі. Фазовий портрет має особливі точки, до яких прагнуть або від яких йдуть фазові траєкторії системи (їх може бути декілька).

Абсолютна стійкість нелінійної системи

Стійкість що не залежить від конкретного типу нелінійності

Причини виникнення автоколивань

Автоколивання залежать від властивостей самої системи і не залежать від початкових умов наприклад від початкового запасу енергії

Поняття цифрової системи керування

Цифрові системи автоматичного керування - це системи, в яких безперервні сигнали перетворюються в цифрові коди і керування здійснюється з використанням алгоритмів обробки цифрової інформації.

Екстраполятор нульовою порядку

Екстраполятор нульового порядку. При реалізації імпульсних систем керування на основі мікро ЕОМ після імпульсного модулятора встановлюють демодулятор або формуючий елемент, який фіксує вихідний сигнал імпульсного модулятора на весь період квантування То неперервного сигналу. Такі формуючі елементи називаються екстраполяторами або фіксаторами нульового порядку.

ЦАП.АЦП

Цифро-аналоговый преобразователь (ЦАП) — устройство для преобразования цифрового (обычно двоичного) кода в аналоговый сигнал (ток, напряжение или заряд). Цифро-аналоговые преобразователи являются интерфейсом между дискретным цифровым миром и аналоговыми сигналами.

Аналого-цифровой преобразователь[1][2][3] (АЦП, англ. Analog-to-digital converter, ADC) — устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал). Обратное преобразование осуществляется при помощи ЦАП (цифро-аналогового преобразователя, DAC).

Как правило, АЦП — электронное устройство, преобразующее напряжение в двоичный цифровой код. Тем не менее, некоторые неэлектронные устройства с цифровым выходом, следует также относить к АЦП, например, некоторые типы преобразователей угол-код. Простейшим одноразрядным двоичным АЦП является компаратор.

Дискретне перетворення Лапласа

Теорема Котельникова  если аналоговый сигнал   имеет финитный (ограниченный по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой строго большей удвоенной верхней частоты  :

z- перетворення

Z-перетворення, як і багато інтегральні перетворення, може бути задано як одностороннє і двостороннє

Замкнуті дискретні системи

Аналіз стійкості на z-площині

Штучні нейронні мережі - причини застосування дозволяють з успіхом вирішувати проблеми розпізнавання образів, виконання прогнозів, оптимізації, асоціативній пам'яті і керування. Традиційні підходи до рішення цих проблем не завжди надають необхідну гнучкість. Багато застосувань виграють від використання нейромереж.

Штучні нейромережі є електронними моделями нейронної структури мозку, який головним чином навчається з досвіду. Природній аналог доводить, що множина проблем, які поки що не підвладні розв'язуванню наявними комп'ютерами, можуть бути ефективно вирішені блоками нейромереж.