Механізація – напрямок технічного прогресу, спрямований на заміну фізичної праці людини, роботою машин і механізмів.

Механізація – процес впровадження машин і механізмів у виробництво.

Автомат – пристрій, що виконує деякий процес без безпосередньої участі людини

Автоматизація - напрямок технічного процесу спрямований на заміну фізичної і розумової діяльності людини на роботу самодіючих систем. Також це процес впровадження у виробництво машин і механізмів.

Автоматичні системи керування – системи, що функціонують без безпосередньої участі людини.

Автоматизовані системи керування - системи, в яких як обов’язковий елемент, бере участь людина оператор.

Автоматичне керування – сукупність дій, які спрямовані на здійснення технологічного процесу, або операцій за певним законом без безпосередньої участі людини.

Математична модель - система математичних співвідношень, яка описує суттєві властивості системи, або процесу, що вивчається.

Теорія автоматичного керування – замість реальних об’єктів розглядає адекватні їм математичні моделі.

Автоматика – це галузь науки і техніки, що вивчає теорію та принципи побудови систем управління об’єктами, що функціонують без безпосередньої участі людини.

Автоматична система – це комплекс апаратних і програмних засобів, призначений для управління різними процесами в рамках технологічного процесу, виробництва, підприємства.

Автоматичне регулювання – автоматичне підтримання сталості будь-якої фізичної величини, характеризує технологічний процес, або її зміну по заданому закону (програмне регулювання), або відповідно до виміряним зовнішнім процесом.

Задавальна дія (вхідна) – дія, що надає інформацію про задачі керування (задає людина оператор, або керувальний пристрій).

Керуюча дія (регулююча) – дія, що безпосередньо діє на об’єкт керування.

Керовані величин – сукупність вихідних фізичних величин, що характеризують стан об’єкту (параметри або координати) які в наслідок процесу керування мають набути заданих значень.

Регульована величина – фізичний параметр, який цілеспрямовано змінюється, або зберігається незмінним в процесі керування.

Збурення – зовнішні дії на систему автоматичного керування, які порушують встановлений зв'язок між вхідними діями і вихідними параметрами.

Принцип розімкненого керування – полягає в тому, що вхідна дія перетворена керуючим пристроєм на керуючу дію і безпосередньо впливає на об’єкт.

Принцип керування за відхиленням – полягає в тому, що відхилення регульованого параметру від заданого значення викликає дію регулюючого органу направленого на зменшення цього відхилення.

Регулювання за збуренням – полягає в тому, що в результаті вимірювання одного або кількох збурень формується дія, яка коректує керуючу дію для компенсації впливу цих збурень на керовану величину.

Комбіноване керування – є поєднанням принципів керування за відхиленням і збуренням в одній системі автоматичного керування.

Одномірні системи керування – системи, стан яких визначається одним вихідним і вхідним параметром.

Багатовимірні системи – системи, стан яких визначається багатьма вихідними параметрами і багатьма вхідними діями.

Багатоконтурні системи автоматичного керування – це системи, які мають два і більше замкнутих контурів передачі дії.

Незв’язні системи автоматичного керування – це система, яка містить кілька самостійних керуючих пристроїв, кожний з яких керує однією, незалежно від інших регульованих параметрів величиною.

Зв’язна система – система яка містить внутрішні зв’язки між керованими величинами.

Складні системи керування – узагальнена назва систем, які неможливо описати коректно математично, які містять велику кількість елементів пов’язаних між собою невідомим чином, в яких невідома природа явищ, що відбувається.

Лінійна система – система, властивості яких не залежать від величини вхідної дії. Для лінійних систем справедливий принцип суперпозиції та гомогенності.

Нелінійні системи – системи, властивості яких залежать від величини вхідної дії. Для нелінійних систем принцип суперпозиції і гомогенності не виконуються.

Стаціонарні системи – системи які не змінюють властивостей зі зміною часу.

Нестаціонарні системи – системи, що змінюють свої властивості зі зміною часу.

Системи автоматичної стабілізації – системи, які призначені для автоматичного підтримання з заданою точністю постійного значення керованої величини.

Системи програмного керування (регулювання) – системи, які призначені для автоматичної зміни з заданою точністю керованого параметру за попередньо заданим законом у функції часу або координат.

Слідкуючі системи автоматичного керування – системи, які призначені для автоматичної зміни з заданою точністю керованої величини у відповідності з попередньо невідомою функцією часу, що визначається вхідною дією.

Розімкнені системи автоматичного керування – системи, коли керуючі дії виробляються без урахування значення керованої величини, яке досягається в результаті керування.

Замкнуті системи автоматичного керування – системи автоматичного керування, в яких керуюча дія виробляється з урахуванням значення керованої величини, яка досягається в результаті керування.

Автоматичні системи неперервної дії – системи в яких зміна регулюючих величин веде до неперервної передачі дії по всьому замкнутому колу (Аналогові системи).

Автоматичні системи дискретної дії – системи, в яких передається та перетворюється сигнал, квантований, може набувати певного рівня, або існувати в певний час.

Цифрові системи автоматичного керування – системи, в яких керуюча дія (сигнал) квантований за часом і амплітудою, відображається у вигляді коду.

Призначення задавального пристрою – ЗП пристрій, який служить для перетворення задавальної дії в сигнал, придатний для подальшої роботи системи.

Призначення регулятора (Р) – пристрій, який служить для реалізації необхідного закону керування.

Призначення виконавчого пристрою (ВП) – безпосередньо діє на об’єкт автоматичного керування.

Призначення датчиків – датчик, елемент системи, що перетворює інформацію про фізичну величину в сигнал, зручний для використання і перетворення в системах автоматичного контролю та керування.

Підсилювач – пристрій, який служить для кількісного перетворення за величиною, або потужністю.

Підсилювач рівня – якщо підсилення здійснюється тільки на величину сигналу, то для роботи такого підсилювача не потрібне споживання зовнішньої енергії. При цьому потужність сигналу на виході підсилювача виявляється меншою, ніж на вході внаслідок втрат її на самому підсилювачі.

Підсилювач потужності - використовуються щоб потужність виявилась достатньою для керування виконуючим пристроєм. Тому такі підсилювачі вимагають для своєї роботи споживання зовнішньої енергії. Якщо сигнал, який поступає на вхід підсилювача і сигнал, потрібний для керування виконуючим пристроєм відрізняють за фізичною природою, в функції підсилювача входить також і перетворення сигналів.

Статичний аналіз системи автоматичного керування – дослідження умов забезпечується рівноважними (усталеними) сигналами, тобто статичні характеристики системи.

Динамічний аналіз системи автоматичного керування – дослідження САР при порушені рівноважного стану процесу.

Стійкість системи керування – це якість, що дозволяє системі витримувати зміни параметрів зовнішнього середовища, відмінна від розрахункових. Систему можна назвати стійкою, якщо вона може впоратися з варіаціями в операційному середовищі з мінімальними збитками, зміною, або втратою функціональності.

Якість системи керування (час регулювання, швидкодія) - Якість САК визначається як загальний показник відповідності системи установленим нормам. Час регулювання – час, по закінченню якого відхилення перехідної характеристики від сталого значення стає й залишається менше заданої величини від сталого значення (0.5%) – визначає швидкодію САК.

Узагальнена характеристика динамічних властивостей САР, яка визначається поведінкою системи як в перехідних процесах, так і в усталеному режимі.

Ланка САР – елемент САР,що розглядається з точки зору його динамічних властивостей і відбиває фізичні властивості реальних органів, їх частин або сукупності органів перетворювати або передавати в прямому напрямку сигнал.

Аперіодичною(інерційною) наз. ланку, в якій при подачі на вхід ступінчатой дії вихідна величина аперіодично прямує певного усталеного значення:w(s)=k/(Ts+1), Т – постійна часу, к- коефіцієнт передачі.

Точність відпрацювання задавальної дії визначається як різниця між заданим значенням регульованої величини і отриманим в процесі регулювання. Е(t)=Y(t)-X(t) або d=lim(Xвх(t)-Xвих(t)) при t->нескінченності.

За Лапласом: s->0 d=lim(s(Xвх(s)-Xвих(s)))=lim(s(c/s-c/s*G(s)/H(s)))=c lim((H(s)-G(s))/H(s))=c (1-b0/a0)

Точність роботи в умовах дії збурень визначається як різниця між значенням регульованої величини при відсутності збурень і значенням регульованої величини при наявності збурень. Е(t)=Y(t)-Y(0) або d(t)=lim(Xвх(t)-Xвих(t0)) при t->нескінченності

В зобр за Лапласом :s->0 d=lim(sXвих(s))*lim(s*(c/s)*(L(s)/M(s))=c lim(L(s)/M(s))=c(d0/f0)

Частотні характеристики САК . Если задана передаточная Функция W(S), то путём подставки S=j получаем частотную передаточную функцию W(j), которая является комплексным выражением т.е. , где А() вещественная составляющая , а К() мнимая составляющая. Частотная передаточная функция может быть представлена в показательной форме:

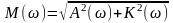
где - модуль;

-аргумент частотной

передаточной функции

Функция М(), представленная при изменении частоты от 0 до  получило название амплитудной частотной характеристики (АЧХ).

Функция (), представленная при изменении частоты от 0 до  называется фазовой частотной характеристикой (ФЧХ)

Частотная передаточная функция W(j) может быть представлена на комплексной плоскости. В этом случае для каждой из частот в диапазоне от 0 до  производится определение вектора на комплексной плоскости и строится годограф вектора. Годограф будет представлять собой амплитудно-фазовую частотную характеристику (АФЧХ). Таким образом, для определенной частоты имеем век­тор на комплексной плоскости, который характеризуется модулем М и аргументом . Модуль представляет собой численное отношение амплитуды выходного гармонического сигнала к амплитуде входного. Аргумент представляет собой сдвиг по фазе выходного сигнала по отношению к входному. При этом отрицательный фазовый сдвиг пред­ставляется вращением вектора на комплексной плоскости по часовой стрелке относительно вещественной положительной оси, .а положительный фазовый сдвиг представляется вращением против часовой стрелки.

Логарифмічні частотні характеристики. Для упрощения графического представления частотных характерис­тик, а также для облегчения анализа процессов в частотных областях используются логарифмические частотные характеристики: логарифмическая амплитудная частотная характеристика (л.а.ч.х.) и логариф­мическая фазовая частотная характеристика (л.ф.ч.х.). При построе­нии логарифмических характеристик на шкале частот вместо  откладывается lg и единицей измерения является декада.

Де­кадой называется интервал частот, соответствующий изменению час­тота в 10 раз. При построений л.а.ч.х. на оси ординат единицей из­мерения является децибел, который представляет собой соотношение L=20 lg M(). Для л.ф.ч.х. на оси частот используется логарифмический масштаб, а для углов - натуральный масштаб. На практике логарифмические частотные характеристики строятся на совмещённой системе координат, которые представлены на рис. 3.1.

БЕЛ – одиниця підсилення або послаблення сигналу, що дорівнює десятковому логарифму десятикратного підсилення вхідного сигналу за потужністю.децибел=0,1 бела. Октава – зміна частоти в 2 рази.

Діаграмми Боде. Запас стійкості.

 

   

 

В условиях эксплуатации параметры системы по тем или иным причинам могут меняться в определенных пределах (старение, температурные колебания и т.п.). Эти колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать САУ так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости.

Согласно критерия Найквиста, чем дальше АФЧХ от критической точки (-1, j0), тем больше запас устойчивости. Различают запасы устойчивости по модулю и по фазе.

Запас устойчивости по модулю характеризует удаление годографа АФЧХ разомкнутой САУ от критической точки в направлении вещественной оси и определяется расстоянием h от критической точки до точки пересечения годографом оси абсцисс (рис.75).

Запас устойчивости по фазе характеризует удаление годографа от критической точки по дуге окружности единичного радиуса и определяется углом  между отрицательным направлением вещественной полуоси и лучом, проведенным из начала координат в точку пересечения годографа с единичной окружностью.

К ак уже отмечалось, с ростом коэффициента передачи разомкнутой САУ растет модуль каждой точки АФЧХ и при некотором значении K = K_кр АФЧХ пройдет через критическую точку (рис.76) и попадет на границу устойчивости, а при K > K_кр замкнутая САУ станет неустойчива. Однако в случае “клювообразных” АФЧХ (получаются из-за наличия внутренних обратных связей) не только увеличение, но и уменьшение K может привести к потере устойчивости замкнутых САУ (рис.77). В этом случае запас устойчивости определяется двумя отрезками h₁ и h₂, заключенными между критической точкой и АФЧХ.

Обычно при создании САУ задаются требуемыми запасами устойчивости h и  , за пределы которых она выходить не должна. Эти пределы выставляются в виде сектора, вычерчиваемого вокруг критической точки, в который АФЧХ разомкнутой САУ входить не должна (рис.78).

10.3. Анализ устойчивости по лчх

 Оценку устойчивости по критерию Найквиста удобнее производить по ЛЧХ разомкнутой САУ. Очевидно, что каждой точке АФЧХ будут соответствовать определенные точки ЛАЧХ и ЛФЧХ.

Пусть известны частотные характеристики двух разомкнутых САУ (1 и 2), отличающихся друг от друга только коэффициентом передачи K₁ < K₂. Пусть первая САУ устойчива в замкнутом состоянии, вторая нет.(рис.79).

 

 

Если W₁(p) - передаточная функция первой САУ, то передаточная функция второй САУ W₂(p) = K W₁(p), где K = K₂/K₁. Вторую САУ можно представить последовательной цепочкой из двух звеньев с передаточными функциями K (безынерционное звено) и W₁(p), поэтому результирующие ЛЧХ строятся как сумма ЛЧХ каждого из звеньев.

Поэтому ЛАЧХ второй САУ: L₂( ) = 20lgK + L₁( ),

а ЛФЧХ:  ₂( ) = ₁( ).

Пересечениям АФЧХ вещественной оси соответствует значение фазы   = - . Это соответствует точке пересечения ЛФЧХ   = -  линии координатной сетки. При этом, как видно на АФЧХ, амплитуды A₁( ) < 1, A₂( ) > 1, что соответствует на САЧХ значениям L₁( ) = 20lgA₁( ) < 0 и L₂( ) > 0.

Сравнивая АФЧХ и ЛФЧХ можно заключить, что система в замкнутом состоянии будет устойчива, если значению ЛФЧХ   = -  будут соответствовать отрицательные значения ЛАЧХ и наоборот. Запасам устойчивости по модулю h₁ и h₂, определенным по АФЧХ соответствуют расстояния от оси абсцисс до ЛАЧХ в точках, где   = - , но в логарифмическом масштабе.

Особыми точками являются точки пересечения АФЧХ с единичной окружностью. Частоты  _c1 и  _c2, при которых это происходит называют частотами среза.

В точках пересечения A( ) = 1 = > L( ) = 0 - ЛАЧХ пересекает горизонтальную ось. Если при частоте среза фаза АФЧХ  _c1 > -  (рис.79а кривая 1), то замкнутая САУ устойчива. На рис.79б это выглядит так, что пересечению ЛАЧХ горизонтальной оси соответствует точка ЛФЧХ, расположенная выше линии  = - . И наоборот для неустойчивой замкнутой САУ (рис.79а кривая 2)  _c2 < - , поэтому при   =  _c2 ЛФЧХ проходит ниже линии   = - . Угол  ₁ =  _c1-(- ) является запасом устойчивости по фазе. Этот угол соответствует расстоянию от линии   = -  до ЛФЧХ.

Исходя из сказанного, критерий устойчивости Найквиста по логарифмическим ЧХ, в случаях, когда АФЧХ только один раз пересекает отрезок вещественной оси [- ;-1], можно сформулировать так: для того, чтобы замкнутая САУ была устойчива необходимо и достаточно, чтобы частота, при которой ЛФЧХ пересекает линию   = - , была больше частоты среза.

 

 

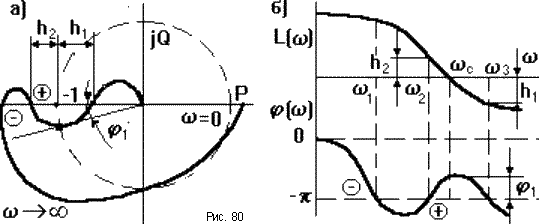
Если АФЧХ разомкнутой САУ имеет сложный вид (рис.80), то ЛФЧХ может несколько раз пересекать линию   = - . В этом случае применение критерия Найквиста несколько усложняется. Однако во многих случаях данной формулировки критерия Найквиста оказывается достаточно.