3. Графічний диктант «Так чи ні?».

«Хоч слова «так» і «ні» короткі, все ж вони вимагають серйозних роздумів».

Піфагор

Властивості функцій. За даним графіком визначити правильне твердження чи ні.

У чні креслять трикутник з вершиною вгору, якщо твердження правильне і вершиною вниз, якщо неправильне.

Твердження для диктанту:

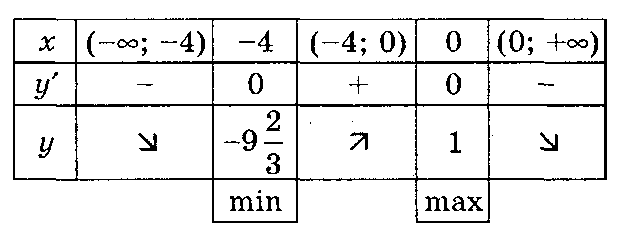
1. Дана функція має три критичні точки;

2. Функція має мінімум в точці х=5;

3. Функція має максимум в точці х=-5;

4. Функція зростає на проміжках [-5; 5] і [ 11; ∞];

5. Функція cпадає на проміжках [-∞; -5] і [ 5; 11];

6. Дана функція парна;

7. Її графік симетричний відносно осі ОУ;

8. Нулі функції: У= -3;

9. На проміжках (-∞; -5) і ( 5; 11) f '(х) < 0;

10)На проміжках (-5; 5) і ( 11; ∞) f '(х) > 0.

Самоперевірка графічного диктанту.

Ключ для перевірки проектується на екран:

V. Застосування знань, закріплення вмінь і навичок при розв’язуванні вправ.

«Теорія без практики мертва і безплідна, практика без теорії неможлива». Рене Декарт.

Робота в групах. Дидактична гра «Шифрувальники».

Учні об’єднуються в 2 команди. Кожна команда отримує графік функції. Необхідно «зашифрувати» його за допомогою описування властивостей даної функції, достатніх для побудови графіка функції:

1. Проміжки спадання;

2. Проміжки зростання;

3. Нулі функції;

4. Координати точок максимуму;

5. Координати точок мінімуму;

6. Координати точки перетину графіка з віссю ОУ.

Команди обмінюються «шифровками» і кожна з команд за описаними властивостями функції будує її графік. Після цього побудований графік звіряється зі зразком.

За правильне «шифрування» члени команд отримують по 1 балу, за правильне розшифрування – по2 бали.

Vі. Контроль знань, умінь і навичок учнів.

Диференційована самостійна робота.

Дослідити функцію за допомогою похідної та побудувати її графік.

Учні самі вибирають завдання.

(Для учнів зі слабкими знаннями дозволяється допомога вчителя: за відповідь вчителя на кожне питання знімається 1 бал).

За правильно виконане завдання І або ІІ варіанту учень отримує 4 бали, а ІІІ або ІV – 6 балів.

В-І.

В-ІІ. у = х⁴ - 2х² - 3

В-ІІІ.

В-ІV. у = 1 – 2х² – .

Розв’язання завдань.

В-І.

1. D(y)=R

2. Знаходимо нулі функції:

і

3. Визначаємо парність: функція ні парна, ні непарна, неперіодична

4.

,

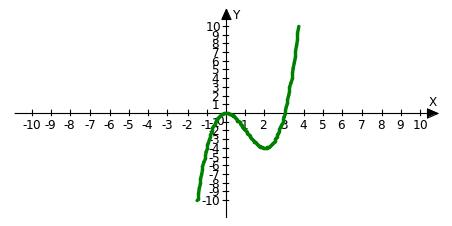, - критичні точки

5.

f

f'(-1)=3·(-1)²-6·(-1)>0

f'(1)=3·1²-6·1<0

f'(3)=3·3²-6·3>0

x=0 – точка максимуму

x=2 – точка мінімуму

f_min=f(0)=0

f_max=f(2)= 23-3·²=-4

6. Будуємо ескіз графіка

В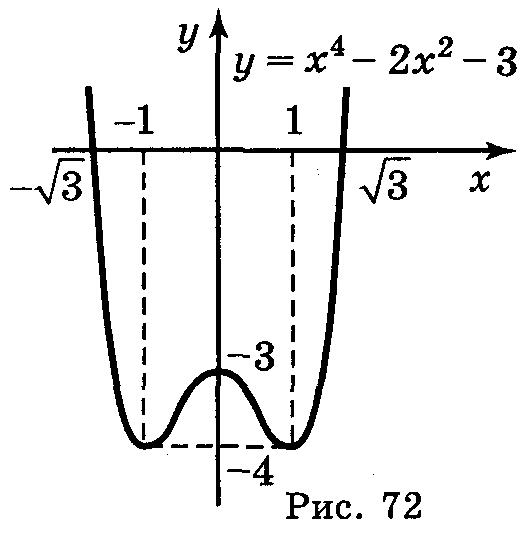 -ІІ. у = х⁴ - 2х² – 3

В-ІІІ.

1. D(y)=R

2. Знаходимо нулі функції:

x=0 і x=1 і x= -1

3. - графік симетричний щодо осі Оу.

4.

, ,

і й - критичні точки

5 .

f

f'(-2)=4(-2) 3-²(-2)<0

f'(2)=4·2³-2·2>0

і - точки мінімуму

х=0 – точка максимуму

6. Будуємо ескіз графіка.

В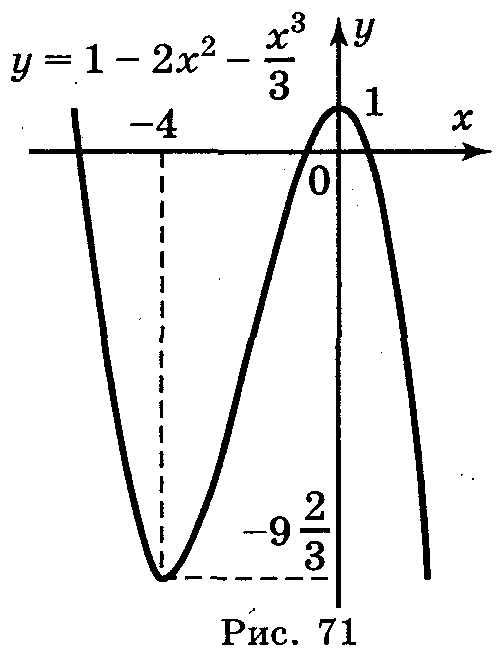 -ІV. у = 1 – 2х² – .